复杂网络理论在“电力电子技术”教学中的应用
2012-10-12韦笃取丘东元
韦笃取,丘东元,张 波
(1广西师范大学电子工程学院,广西桂林541004 2华南理工大学电力学院,广东广州510641)
0 引言
由若干个节点与连接不同节点之间的一些边组成的对象称为网络,如果用节点来表示不同的个体,边表示不同节点之间所具有的某种关系,就可以把大量实际系统抽象为一个网络。如果这些网络节点和边的数量众多,结构复杂,连接形式多样,我们就称其为复杂网络。自从Watts和Strogatz于1998年提出小世界网络(Small World Network,简称SWN)模型以及Barabasi和Albert于1999年提出无标度网络(Scale-Free Network,简称SFN)模型以来[1,2],作为一种交叉性学科,复杂网络理论发展很快,已经在很多领域得到应用。从Internet到WWW,从电力网络到交通网络,从科研合作网络到经济、政治和社会关系网络等都有发展。可以说,人们已经生活在一个充满着各种各样的复杂网络世界中,对复杂网络的定量与定性特征的科学理解已成为网络时代科学研究中一个挑战性课题,甚至被称为网络的新科学(New Science of Networks)[3,4]。
另一方面,“电力电子技术”是高校电气工程及其自动化专业、电气信息专业本科生的专业必修课程之一。课程的主要内容包括电力电子器件、电力电子电路及控制技术[5,6]。传统电力电子技术教学方法是把系统分解为大量的基本单元(如独立电子元器),由这些基本单元的性质及其相互作用按照电路学理论进行计算,再把计算结果综合起来,推断系统的整体性质。最近通过实证研究,学者发现电力电子系统是一个典型的复杂网络[7,8]。这种复杂网络理论为“电力电子技术”的教学开创了一条新路,就是用整体论方法处理复杂系统问题。新方法把电路定理与统计处理结合起来,把定量规律与定性特征结合起来,把系统的分解与单元的聚合结合起来,在处理复杂系统的结构与性质、机理与演化等问题上取得了重要进展。电力电子技术的进一步发展需要吸取复杂网络的营养。本文将就复杂网络与“电力电子技术”教学的关系与应用进行探讨,并通过一个具体实例对此问题进行分析。
1 复杂网络的几个基本概念
1.1 平均路径长度
网络中两个节点i和j之间的距离dij定义为连接这两个节点的最短路径上的边数。网络中任意两个节点间距离的最大值称为网络直径(Diameter)记为

任意两个节点之间距离的平均值定义为网络的平均路径长度
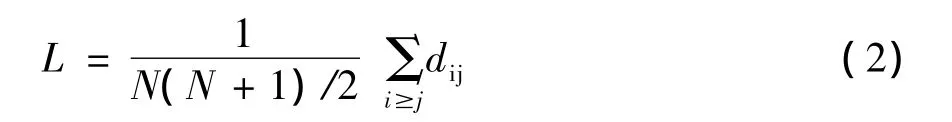
式中,N为网络节点数。网络的长度L也称为网络的特征路径长度(Characteristic Path Length)。
1.2 聚类系数[3,4]
一般地,假设网络中的一个节点i有ki条边将它和其它节点相连,这ki个节点就称为节点的邻居。在这ki个节点之间最多可能有ki(ki-1)/2条边。而这ki个节点之间实际存在的边数Ei和总的可能的边数ki(ki-1)/2之比就定义为节点i的聚类系数:
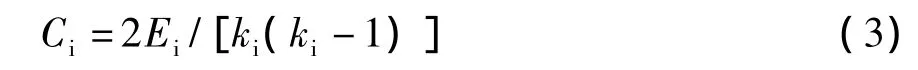
从几何特点看,上式的一个等价定义为

这里以节点i为中心的三元组,是指包含节点i的三个节点,并且至少存在从节点i到其它两个节点的两条边。整个网络的聚类系数C就是所有节点的聚类系数Ci的平均值。很明显,0C1。当且仅当所有的节点均为孤立节点,即没有任何连接边时,C=0。当且仅当网络是全局耦合的,即网络中任意两个节点都直接相连时,C=1。对于一个含有N个节点的完全随机的网络,当N很大时,则有C=O(N-1)。而许多大规模的实际网络都具有明显的聚类效应,它们的聚类系数尽管远小于1但却比O(N-1)要大得多。事实上,在很多类型的网络(如社会关系网络)中,你的朋友的朋友同时也是你的朋友的概率会随着网络规模的增加而趋向于某个非零常数,即当N→∞时,C=O(1)。这意味着这些实际的复杂网络并不是完全随机的,而是在某种程度上具有类似于社会关系网络中“物以类聚,人以群分”的特性。
1.3 度与度分布[3,4]
度(Degree)是单独节点的属性中简单而又重要的概念。节点i的度k定义为与该节点连接的其它节点的数目。有向网络中一个节点的度分为出度(Out-Degree)和入度(In-Degree)。节点的出度是指从该节点指向其它节点的边的数目,节点的入度是指从其它节点指向该节点的边的数目。直观上看,一个节点的度越大就意味着这个节点在某种意义上越重要。
网络中所有节点i的度ki的平均值称为网络的(节点)平均度,记为〈k〉。网络中节点的度的分布情况可用分布函数P(k)来描述。P(k)表示的〈k〉是一个随机选定的节点的度恰好为k的概率。
规则的格子有着简单的度序列:因为所有的节点具有相同的度,所以其度分布为Delta分布,它是单个尖峰。网络中的任何随机化倾向都将使这个尖峰的形状变宽。完全随机网络的度分布近似为Poisson分布,其形状在远离峰值〈k〉处呈指数下降。这意味着当k〈k〉时,度为k的节点实际上是不存在的。因此,这类网络也称为均匀网络。
近几年的大量研究表明,许多实际网络的度分布明显地不同于Poisson分布。特别地,许多网络的度分布可以用幂律形式P(k)~k-γ来更好地描述。幂律分布曲线比Poisson指数分布曲线下降要缓慢得多。幂律分布也称为无标度(Scale-Free)分布,具有幂律度分布的网络也称为无标度网络,在一个度分布为具有适当幂指数(通常为2γ3)幂律形式的大规模无标度网络中,绝大部分节点的度相对很低,但存在少量的度相对很高节点。因此,这类网络也称为非均匀网络(Inhomogeneous Network),而那些度相对很高的节点称为网络的“集线器”(Hub)。
2 复杂网络理论的具体应用例子
我们现在通过一个典型的例子,即对三相逆变电路器件短路时的故障诊断,来说明复杂网络方法在“电力电子技术”教学中的应用。
一般来说,我们首先根据网络的结构特点,建立电力电子变换器的复杂网络模型,具体方法如下:在电力电子变换器中,将元器件(如电阻、电容、电感、开关器件、二极管和变压器等)及电源定义为节点,将连接各个元器件的导线定义为无向边,由此得到电力电子变换器对应的网络图。
图1为三相桥式逆变器,其网络模型如图2(a)所示。图中共有节点数N4a=10个,边数l4a=24条,对应的基本特征参数为:聚类系数C4a=0.46,平均路径长度L4a=1.467条。而对于一个具有相同节点数和边数的随机网络,其聚类系数和平均路径长度分别为Crand≈0.38,Lrand≈1.468条。对比两组数据,可得C4a>Crand,L4a≈Lrand。可见三相桥式逆变器的主电路符合小世界网络“大聚类系数和小平均路径长度”特性[8],因此属于一种典型的小世界网络。

图1 三相桥式逆变器
假设晶闸管T1断路,那么将节点T1剔除,并删除T1与其他节点相连的边,得到图2(b)。此时N4b=9个,l4b=19条,C4b=0.456,L4b=1.472条。对比图2(a)和2(b),发现C4a≈C4b,L4a≈L4b,即故障发生后,虽然网络模型中的节点和边均减少,但其特征参数基本不变。因此采用现有的建模方法,只能表达元器件之间的静态连接关系,不能反映出逆变器的运行状况,而且难以区分正常态和故障态。

图2 故障发生前后对比
三相桥式逆变器正常工作时,共阴极组和共阳极组各有一个晶闸管导通,设T1和T6导通。此时负载Ra和Rb直接与电容C相连,若添加两条连线(虚线)反映此电气连接关系。正常运行(T1与T6导通)时,图2(a)便演变成为图3(a)。由于三相桥的对称性,图3(a)也适用于其余五对晶闸管导通时的情况,因此,图3(a)可以看作三相桥式逆变器正常工作模态对应的网络图。当晶闸管T1断路时,逆变器的输出电压缺相,故障态与正常态相互转换,相当于在图3(b)和图3(c)之间切换。
图3(b)是T1断路,仅有T6导通的状态。图3(c)是T1断路,T2和T3导通的状态。我们现在来计算上述各图的特征参数可得:由图3(a)得C5a=0.523,L5a=1.422条;由图3(b)得C5b=0.485,L5b=1.444条;由图3(c)得C4c=0.543,L4c=1.417条。分析可见,图3(a)和图3(c)对应的特征参数基本相等,其中ΔC=0.4%,ΔL=3.8%;而图3(b)和图3(c)对应的特征参数变化率达到,ΔC=1.9%,ΔL=10.7%这意味着T1断路时,当逆变器在(图3(c))所示有输出电压时,其网络特征与原正常态的基本相同;而当逆变器在(图3(b))所示无输出电压时,其网络特征出现了较明显的变化。
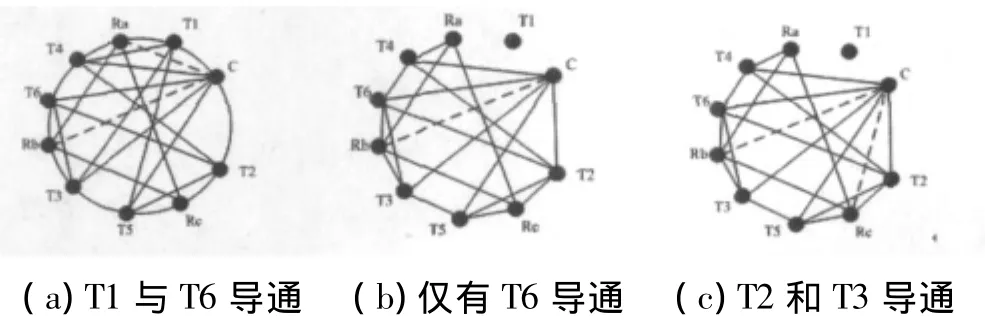
图3 三相桥式逆变器的网络图
由此可见,采用合适的建模方法,电力电子系统的不同故障能够在系统结构层次上体现。即使是同类故障,对应的网络图相似,还可以利用网络结构的唯一性,采用其他特征参数(如节点对应的聚类系数、度分布函数等)进行更细致的区分。因此,本例子运用复杂网络理论进行故障诊断的教学,可以取得预期的效果。
3 结语
本文应用复杂网络方法可以解决“电力电子技术”教学中的难题。复杂网络在电力电子教学上的应用还远远不止上述一个例子。我们还可以应用复杂网络思想和方法去解决复杂电力电子技术其他方面的问题。复杂网络方法更多的应用需要我们进一步探讨。
[1] Watts D J,Strogatz S H.Collective dynamics of'small world'networks[J] .Nature,1998
[2] Barabási A L,Albert R.Emergence of scaling in random networks[J] .Science,1999
[3] 汪小帆,李翔,陈关荣.复杂网络理论及其应用[M] .北京:清华大学出版社,2006
[4] 周涛,柏文洁,汪秉宏,刘之景,严钢,复杂网络研究概述[J] .北京:物理,2005
[5] 丘东元,彭锦凤,张波,基于仿真平台的“电力电子技术”教学模式探讨[J] .南京:电气电子教学学报,2009
[6] 丘东元,何文志,张波,肖文勋,基于Flotherm软件的电力电子装置热分析[J] .南京:电气电子教学学报,2009
[7] 丘东元,彭锦凤,张波,电力电子变换器结构性故障的有向图论诊断方法,[J] .哈尔滨:电机与控制学报,2010
[8] 彭锦凤,电力电子变换器的小世界网络特性及其故障分析[J] .广州:华南理工大学,2010
