关于信号系统中的幅度和相位关系
2012-10-12李力利
李力利
(上海交通大学电子工程系,上海200240)
0 引言
在“数字信号处理”课程的教学中会涉及到系统的幅度响应和相位响应之间的关系问题。对于具有有理系统函数的离散时间线性时不变系统,也即由差分方程描述的系统,其幅度和相位之间有某种约束关系。在零点和极点个数已知的情况下,幅度已知则相位的选择有限,反之,相位已知则除了一个加权因子外也仅有有限种幅度可供选择。如果零点和极点个数不加限定,则选择有无穷多种[1]。
文献[1] 只给出了由幅度确定系统函数的方法,没有给出理论依据,很多教师和学生对此都心存疑问,认为结果并不全面。本文针对各种情况进行详细分析,讨论了由相位确定系统函数的方法。
1 根据幅度确定相位
我们给定系统的幅度平方特性为H(ejω),并且已知系统函数H(z)是z的有理函数。我们在下面讨论根据|H(ejω)|2确定系统函数H(z)和其频率响应H(ejω)的方法[1,2]。
1)有理系统函数对应的幅度平方函数
因为H(z)是z的有理函数,所以可以表示成
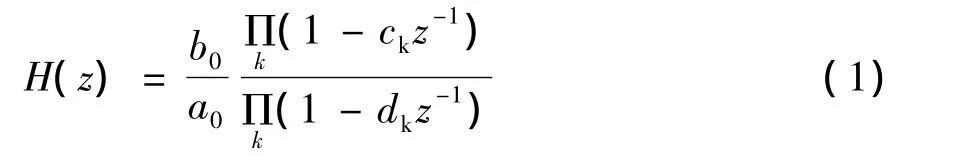
其中,ck和dk是H(z)的零点和极点。我们已经知道频率响应是系统函数在单位圆上的取值,所以有
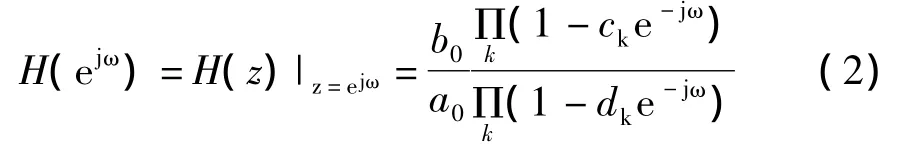
则幅度平方函数具有如下形式:
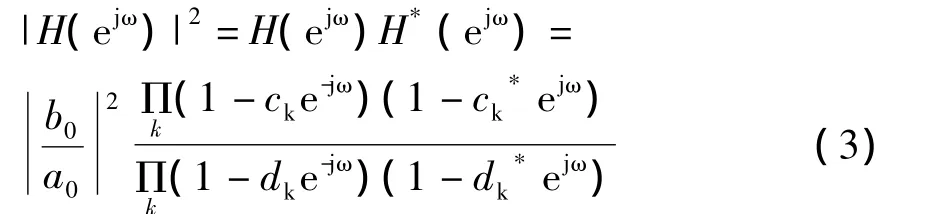
2)由幅度平方函数确定系统函数
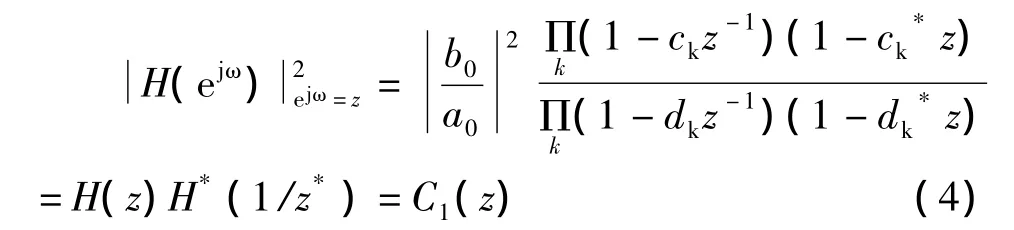
C1(z)的零点是ck和,它们互为共轭反演,极点是dk和,也互为共轭反演。如果H(z)的系数都是实数,则零点四个一组和1/ck互为共轭和反演关系[1,3],位于单位圆上或实轴上的零点则两个一组甚至单独存在。极点的特点也是如此。这些零点和极点分别来自于H(z)和H*(1/z*)。
下面我们讨论一下除了上述方法确定的系统函数,还有没有其他的可能。考虑到|H(ejω)|中的ejω也可能是H(z)中的转换得到的,所以也可以将式(3)的ejω)用1/z*替换以还原系统函数,即有
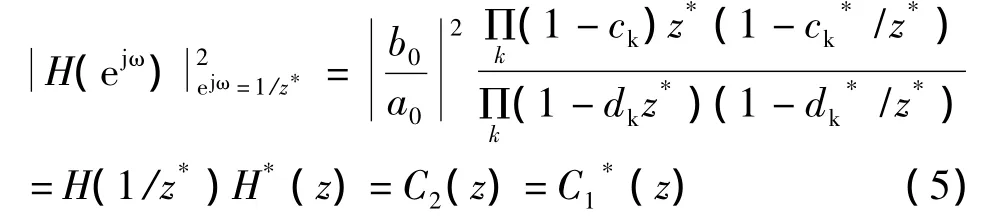
该表达式仅仅是式(4)的共轭,所以C2(z)的零点极点和C1(z)具有相同的特点。将C2(z)的因式分成两部分,其中一部分构成H(z)就得到系统函数的另外一些可能的表达式。比较式(4)和式(5)发现,两种方法得到的H(z)的表达式互为共轭关系。所以两种方法其实就是同一种方法,也就是说,将采用式(4)确定的H(z)取共轭,得到的系统函数也满足给定的幅度响应。
另外,我们还可以令式(3)中的某些ejω=z,另一些ejω=1/z*,得到z的其它有理函数表达式。比如:
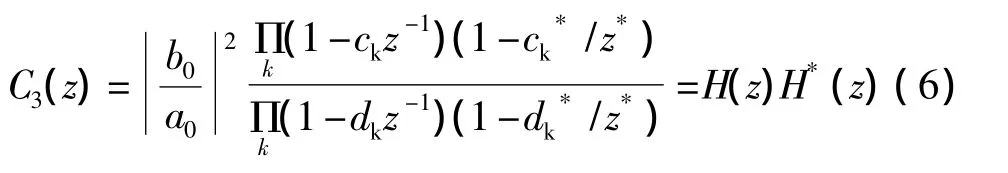
或
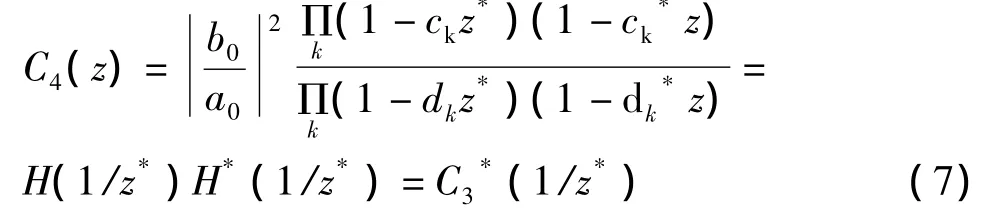
C3和C4的零点和极点全是二阶的。如果H(z)的系数都是实数,则具有互为共轭的二阶零点对和互为共轭的二阶极点对。
式(3)中各因式对在用ejω=z和ejω=1/z*分别进行替换时还可以有不同的组合方式,得到的所有的表达式其实都包括在式(4)得到的结果中。所以,采用式(4)确定的系统函数就涵盖了所有的情况,最多再扩充同等数量的取共轭的系统函数。文献[1] 只给出了这种方法。
如果H(z)的零点和极点个数没有规定,根据以上方法确定的系统H(z)级联任意全通系统Hap(z),得到的新系统[H(z)Hap(z)] 也具有规定的幅度响应,所以H(z)有无穷多种可能选择。
3)由幅度平方函数确定频率响应
按照前面的方法确定了H(z),也就是可以确定H(ejω)。下面再讨论根据直接确定H(ejω)的问题,对这个问题的分析要简单得多。从式(3)看出是ejω的有理函数,并且分子必然是互为共轭的两个因式成对出现,分母亦然。在这些因式对中任取其一进行组合则得到H(ejω)的若干种不同的表达式。如前所述,如果H(z)的系数全是实数,则式(3)可能存在如下形式:
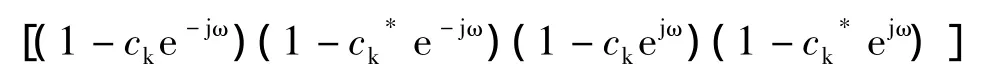
分组时前两项必须一起,后两项必须一起。
同理,这个级联任意全通系统后的频率响应[H(ejω)Hap(ejω)] 也可以是此所求,所以结果可能无穷多。
2 根据相位确定幅度
给定系统的相位响应arg[H(ejω)] ,并且已知系统函数H(z)是z的有理函数。我们下面讨论根据arg[H(ejω)] 确定H(ejω)或H(z)的方法。
我们采用简写符号a(ejω)=tan{arg[H(ejω)] }。因为
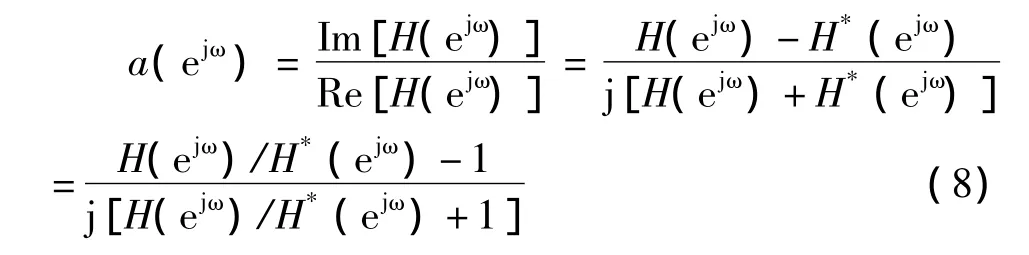
所以,H(z)是z的有理函数的情况下,a(ejω)是ejω的有理函数。由式(8)可以求得
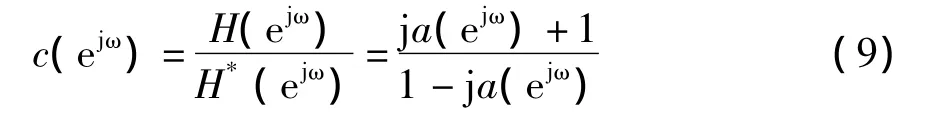
如果H(ejω)具有式(2)的形式,则
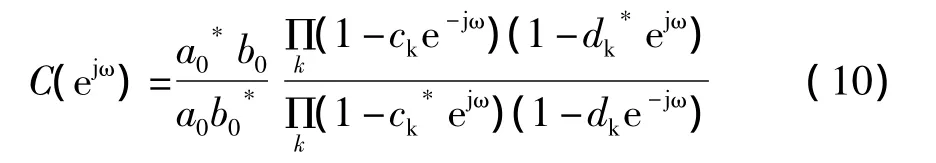
可见C(ejω)也是ejω的有理函数,其分子和分母必然是互为共轭的两个因式成对出现。如果任取其中的一个因式则得到H(ejω)的表达式,比如说取或,结果也是不唯一的。如果H(z)的系数全是实数,则式(10)可能存在形如的因式组,则选取时分子中的两个因式必须同时取舍,分母中的两个因式也必须同时取舍。
我们也可以将式(10)的ejω替换成z,得到
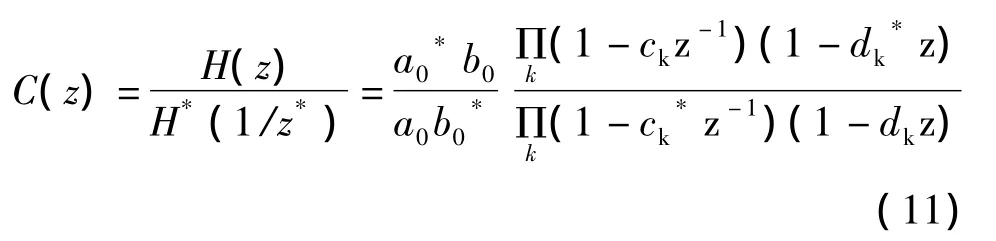
与前面类似地,将C(z)的因式分成两组,得到H(z)的若干种表达式。
另外,根据上述方法求出H(ejω))或H(z)后,级联一个相位为零的系统,得到的新的系统也满足给定的相位。
综上所述,相位给定的情况下,幅度的选择也不是唯一的,在零点极点个数确定的情况下,幅度响应只有有限种可能。
3 结语
本文针对具有有理系统函数的系统,首先分析了由给定的幅度响应确定系统函数的方法,全面考虑了各种情况以验证教材上给出方法的正确性,然后讨论了由幅度响应直接确定频率响应的方法,接下来又讨论了由相位响应确定系统函数和频率响应的方法,从而全面验证了幅度和相位之间存在着某种约束关系。
[1] Alan V.Oppenheim.Discrete-Time Signal Processing(second edition).Prentice Hall,1999
[2] 倪养华,王重玮.数字信号处理-原理与实现.上海:上海交通大学出版社,1998
[3] 刘兴钊,李力利.数字信号处理.北京:电子工业出版社,2010
