确定电力系统临界出口点方法的研究
2012-10-11岳颖,林楠
岳 颖,林 楠
(1.东北电力大学,吉林 吉林132012;2.通辽电业局,内蒙古 通辽028000)
0 引言
目前,在电力系统暂态稳定的分析中,求解稳定平衡点与不稳定平衡点非常重要。特别是应用直接法与Normal Form变换进行暂态稳定分析均是以主导不稳定平衡点(CUEP)为基础的。对于受扰系统,我们一般只研究与故障轨迹相关的那部分稳定域边界(包含CUEP),而求出CUEP上的稳定流形就确定了系统的稳定域边界[1]。求解CUEP的问题首先就是求解系统的不稳定平衡点,也就是求解非线性微分方程组。对于电力系统这个非线性系统,不论是从理论还是计算量方面考虑,直接求解非线性微分方程组很困难,所以主要求出不稳定平衡点附近的近似解便可。
Normal Form变换[2]是一种基于非线性动力学理论的有效的数学工具,这种方法将原始非线性系统的表达式在主导不稳定平衡点处进行泰勒展开后,再经过线性变换和非线性变换,将系统映射到一个线性系统中。原系统的稳定边界在主导不稳定平衡点处经过映射后在线性空间中是一个超平面,当持续故障轨线与稳定边界相交时,对应的交点就是系统临界出口点,进而可以得到临界切除时间。
本文提出的方法是首先将求解主导不稳定平衡点的问题转化为非线性最小二乘问题[3],并采用结构p步牛顿法,在计算的过程中自动调节,保证收敛到正确的CUEP,而后在主导不稳定平衡点处对系统表达式做泰勒展开,并应用Normal Form理论对其进行线性和非线性变换,最后求出临界切除时间。
1 结构p步牛顿法求主导不稳定平衡点
求解主导不稳定平衡点的问题就是求解下列非线性方程组

将其转化为求非线性最小二乘问题,即

其中 θ=(θ1,θ2,…,θn)T∈Rn。
F(θ)的二阶导数(海森矩阵)为

式中,A(θ)为 F(θ)的雅格比矩阵,C(θ)与 S(θ)分别为H(θ)的线性与非线性部分。S(θ)就是求解最小二乘问题中的残量部分,在计算的过程中将会随着主导不稳定平衡点求解过程的变化而变化。因此,在计算的过程中选用合适的算法比较有利于加快收敛速度。
本文选择文献[4]中提出的结构p步牛顿法进行求解。此方法对零残量问题具有二阶收敛速率,而对于大残量问题具有p步p+1阶收敛速率。应用结构p步牛顿法求解CUEP的计算步骤为
1) 给定初始点 q0,令整数 p≥1,k=0。
2)令

其中,i=1,2,…,p -1,参数 p 表示迭代次数,当在θk,0点时,采用牛顿步;当 0 < i< p 时,在 θk,i点采用简化结构牛顿步。
3) 若满足‖F(θk)‖ =0,则输出 θk,得到不稳定平衡点的点列{θk};否则,令k=k+1,转步骤b。
4)用切平面筛选法[5]确定主导不稳定平衡点。
从θk到θk+1的p步中,只需要计算一次就得到S(θk)。其中构造 Bk,i进行求解,大大减少了计算量,并且具有较高的收敛性。
2 三阶Normal Form变换
现有的部分文献为了研究方便,一般省略高阶项,只研究到二阶解析解,使得计算的结果存在不容忽视的截断误差。文献[6-7]将系统的解析解推导到三阶,并验证了三阶解析解比二阶的更加精确。下面结合文献对系统进行三阶Normal Form变换的推导步骤进行介绍。
设非线性系统的微分方程为

式中,X=(x1,x2,…,xn)T∈Rn。将式(2)在主导不稳定平衡点X0处做泰勒展开并保留至三阶项,得

式中,A=[∂Fi/∂X]x0为系统的雅克比矩阵为系统的二阶矩阵的第 i个子矩阵,
求取原非线性系统线性部分X˙=AX的特征值λ1,…,λn。
令线性变换为

式中,U为矩阵A的右特征向量矩阵,V为矩阵A的左特征向量矩阵,且UV=1。将式(4)代入式(3),变换后的Y系统表达式为其中,Vi,j是矩阵 V 的第 i行 j列的元素。
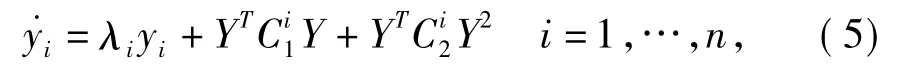

选取非线性变换形式为

其中,非线性变换矩阵为

将式(6)代入式(5)并略去四阶以上项,可得到线性空间的表达式

其中,J是由矩阵A的特征值构成的对角阵,即J=diag(λ1,…,λn)。
3 Normal Form理论在暂态稳定中的应用[8-9]
经过上面Normal Form变换后的系统持续故障轨迹在空间的表达式为

Z空间中的持续故障轨迹与稳定边界的交点就是稳定边界上的出口点,即为临界切除点。稳定边界在Z空间映射为z1=0(设λ1>0),于是,当正实部特征根对应的表达式过零或变号时对应的时间就是临界切除时间。求临界切除时间的具体步骤如下:

表1 新英格兰39节点系统主导不稳定平衡点
1)计算故障前系统的潮流。
2)将系统微分方程写成式(1)的形式,并应用结构p步牛顿法求出故障后主导不稳定平衡点。
3)在主导不稳定平衡点处将系统方程进行泰勒展开,略去四阶以上项,计算矩阵
5)求出持续故障轨线表达式,并将其经过线性变换与非线性变换映射到Z空间,找到正实部特征根对应的轨迹,判断它何时变号,此时对应的时间即为临界切除时间。
4 实例分析
新英格兰39节点系统如图1所示,对其进行仿真验证,线路和发电机数据见文献[10];其发电机采用二阶经典模型,均匀阻尼系数为λ0=-0.2,负荷采用恒阻抗负荷。设系统在表1中所示发生三相接地故障,并切除该线路。
先用结构p步牛顿法求出CUEP,再应用Normal Form变换进行仿真。分别对靠近机端的线路及输电线路中发生故障两种情况进行分析,并与BCU法[11]和 PEBS 法[12]进行比较,结果如表1、表2 所示。根据结果可以看出,当靠近机端线路发生故障时,利用本文的方法所获得的临界切除时间tcr有时产生的误差会较大,但与BCU和PEBS法相比,还是可以接受的;当输电线路上发生故障时,利用本文方法所得的tcr与时域仿真法的结果误差不大,基本上在10%以内,满足工程要求;而基于BCU法和PEBS法所得的结果产生的误差有时候较大。因此,对于输电线路上发生的故障,应用本文方法可以有效估计临界切除时间。

图1 新英格兰39节点系统
5 结论
本文将结构p步牛顿法与Normal Form变换相结合对暂态稳定出口点进行估计。将求CUEP的问题转化为非线性最小二乘问题避免了建立能量函数,同时采用结构p步牛顿法保证了快速收敛到CUEP;应用三阶Normal Form变换保证了临界切除时间计算的快速性和准确性。通过对新英格兰10机39节点系统进行仿真,验证了本文方法的有效性。
[1]HSIAO-DONG C,HIRSCHMW,WU Felix-f.Stability Region of Nonlinear Autonomous Dynamic Systems[J].IEEE Trans on Ac,1988,33(1):16 -27.
[2]THAPARJ,VIJAY,KLIEMANN W,et al.Application of the Normal Form of Vector Fields to Predict Interarea Separation in Power Systems[J].IEEE Trans on Power Systems,1997,12(2):844-850.
[3]李颖晖,张保会,徐成贤.应用开关算法计算电力系统中的主导不稳定平衡点[J].西安交通大学学报,2003,37(4):407-410.
[4]王来生,甄苓.非线性最小二乘问题的结构p步牛顿法[J].西安交通大学学报,2003,37(4):407 -410.
[5]侯凯元,闵勇,张瑞琪.电力系统暂态稳定域边界局部近似方法的研究[J].中国电机工程学报,2004,24(1):1-5.
[6]邓集祥,陈武晖,涂进,等.电力系统3阶解析解的推导及验证[J].中国电机工程学报,2007,27(28):12 -18.
[7]黄琦,王州强,张昌华.基于Normal Form理论的电力系统3阶解析解[J].电子科技大学学报,2009,38(6):957 -961.
[8]李颖晖,张保会.正规形理论在电力系统稳定性研究中的应用(四)—复杂电力系统的稳定边界研究[J].电力自动化设备,2003,23(9):5-8.
[9]邓集祥,谢立汀.多机电力系统暂态稳定分析的一种新方法[J].吉林电力,2004,6(12):9-12.
[10]PAI M A.Energy Function Analysis for Power System Stability[M].Boston(MA,USA):Kluwer Academic Publishers,1989.
[11]HSIAO-DONG C,CHIA -CHIA C.Theoretical foundation of the BCU method for direct stability analysis of network-reduction power system.Models with small transfer conductances[J].Circuits and Systems Fundamental Theory and Applications,IEEE Transactions on,1995,42(5):252 -265.
[12]KAKIMOTO N,OHSAWA Y,HAYASHI M.Transient Stability Analysis of Electric Power System via Lure-Lyapunov Function Part I and II[J].Trans IEE Japan,1978,98(5 -6):63 -79.
