自抗扰控制器参数整定的一种新方法
2012-10-11王东振文新委
王东振,文新委,宋 刚
(1.华能沁北电厂,河南 济源454662;2.华能河南分公司,河南 郑州450016;3.大唐珲春发电厂,吉林 珲春133303)
1 自抗扰控制器参数的整定方法
自抗扰控制器[1]有很多参数需要整定,在跟踪微分器,扩张状态观测器,非线性反馈中都有参数需要整定,并且有些需要对多个参数同时进行整定,即多目标优化。对自抗扰控制器参数的整定,应用比较多的是用遗传算法,这种方法是起始阶段先设定初值,在用遗传算法完成下面的整定,该方法有着收敛速度快,方法简单等优点,同时也存在着不足,即如果目标函数和初值设定选取不当,整定后的参数无法使自抗扰控制器的控制效果令人满意。
本文依据分离原则和过渡过程对跟踪微分器的参数进行了整定,扩张状态观测器用改进的非支配排序遗传算法进行整定[2],最后用非线性最小二乘法对非线性反馈进行整定。
跟踪微分器的参数是随着安排过渡过程时间的长短而变化。因此,在确定了安排过渡过程时间以后,要根据这个时间对跟踪微分器的参数进行整定[3]。在对跟踪微分器的参数整定以后,对扩张状态观测器的参数进行整定,这是一个多目标优化问题,式(1)为多目标函数优化的目标函数式[4]。

2 帕累托解的择优
针对多目标优化,通常产生的解为帕累托解,这就要求我们在这些解集当中选择一个最符合要求的解。这里选用基于模糊理论的帕累托解寻优方法。对解中每个非支配解定义函数值为

式中:Nobj表示目标函数的个数;Mp表示帕累托解中非支配解个数。
在计算出来的解集当中,能使得式(2)的值最大,则说明这个解的综合性最好。所以扩张状态观测器参数的优化结果应该为使式(2)达到最大的解。
3 交叉算子
为了增加改进的非支配排序遗传算法的全局搜索范围,在这里应用算术交叉算子,表达式为

其中,参数c和 d是[-0.2,1.2]之间随机产生的随机数,而且c+d=1。
4 对于复杂对象的整定
在多目标优化中,如果需要优化的对象非常复杂,可以根据经验减少初始选择值的范围,减少运算流程,提高效率。对于没有这方面经验的人员来说,可以通过每次整定的结果逐渐地缩小下一次的初值选取范围,经多次整定最终确定我们所需要的整定结果。
5 综合整定算法实例
选取的控制系统如式(4)所示。

式中,x1和x2为系统的空间状态变量,u为输入,y为输出,Asign[sin(wt)]为系统中的不确定部分和扰动。这里我们定义一个函数:
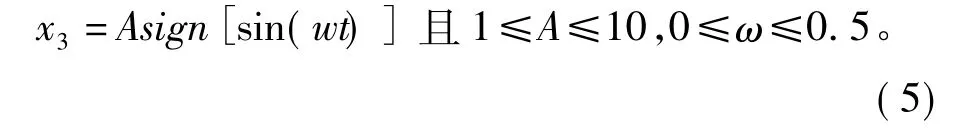
5.1 跟踪微分器参数的整定
跟踪微分器输入为阶跃输入,将过渡时间设为1.4 s,则根据跟踪微分器的整定原则,即可以确定出此跟踪微分器的参数为r=5,跟踪微分器的输出曲线如图1所示,可以看到输出曲线达到稳态时间为1.4 s,且阶跃响应无超调。

图1 跟踪微分器整定曲线
5.2 扩张状态观测器参数的整定
我们所选择的控制对象是二阶系统,它的扩张状态观测器应为三阶,所以,这里选取的优化目标函数为

设定积分步长 h=0.01,迭代次数 gen=20,种群数量为20。根据式(2)进行帕累托解择优,得到应用改进的非支配排序遗传算法对扩张状态观测器的参数整定结果为

图2-图4显示了z跟踪x的效果图。从图2中可以看到,每个图中的两条曲线差别非常小,符合我们的预期目标。

图2 x1-z1观测图
将遗传代数设定为100,对这个扩张状态观测器进行优化,这时,种群都已经变成了非支配解,再次进行帕累托解择优,择优原则即优化参数所对应的优化目标值能够使式(2)最大。这时应用改进的非支配排序遗传算法对扩张状态观测器的参数整定结果为

图5显示了z3跟踪x3的效果图,从图5中可以看出,z3能够很好的跟踪x3,而从图4中可以看到,z3跟踪x3的效果就不如图5明显,因此,可以通过扩大遗传代数来提高优化精度。


图5 z3跟踪x3的效果图
用传统的遗传算法优化结果为[219.2,2603.6,1602.5],x2-z2的观测图如图6所示。从图6中可以看出,z2跟踪x2的效果并不理想。所以,在应用传统遗传算法对扩张状态观测器进行参数整定时,初始值的选取就显得至关重要,就不能用随机的初始值进行优化,这是非常值得注意的一点。
5.3 非线性反馈参数的整定
将已经整定好的跟踪微分器和扩张状态观测器的参数带到自抗扰控制器当中,应用非线性最小二乘法算法对非线性反馈的参数进行优化,设定初值为[1 0]。通过闭环仿真和控制机制,对优化控制器参数进行确认,15步以后可以得到优化结果[1050 39]。此时系统闭环响应曲线如图7所示。

从图7中可以看到,自抗扰控制器的输出曲线与设定值之间差别很小,而跟踪微分器和扩张状态观测器的参数是在前文中整定好的,即说明此处整定的非线性反馈参数满足要求,由此可以得出非线性反馈的参数完全可以应用非线性最小二乘法对其整定。
6 结论
自抗扰控制器有很多参数需要整定,本章根据分离原则,分别讨论了自抗扰控制器各部分的参数整定方法。跟踪微分器根据需要的过渡过程对跟踪微分器的参数进行整定,扩张状态观测器用改进的非支配排序遗传算法进行整定(NSGA_Ⅱ),最后用非线性最小二乘法对非线性反馈进行整定。仿真实例表明,此种参数整定方法,其得到的控制器控制效果具有快速性、稳定性的特点,也优于用遗传算法(GA)对自抗扰控制器参数进行整定的方法。
[1]陈静,武军,郑金华.一种改进的非支配排序多目标遗传算法[J].计算机工程与应用,2009,45(29):60 -63,71.
[2]韩京清.自抗扰控制技术[M].北京:国防工业出版社,2008.
[3]吴猛,朱喜林,鄂世举,等.自抗扰控制器参数整定方法的研究[J].北京理工大学学报,2009,29(2):121 -123,127.
[4]徐莉.基于改进遗传算法的多目标TSP问题研究[D].武汉:武汉理工大学,2008:1-40.
