GPS／GLONASS组合单点定位及精度分析＊

丁建洋，王解先

（同济大学，上海200092）

0 引 言

全球导航卫星定位系统（GNSS）这些年发展迅速，目前GPS在轨卫星达31颗，预计GLONASS 2012年底将有24颗在轨卫星，而GLONASS的M和K型号的卫星设计寿命大幅度的提高，保障了系统持续不间断的全天侯工作状态运行能力［1］。GLONASS卫星定位系统与GPS卫星定位系统相比，可靠性和精度方面还是有一定的差距［2］，若是能实现二者联合定位，可以增加观测卫星的颗数、改善GDOP和PDOP值，从而提高定位精度，更好地满足用户对于定位精度需求。

1 GPS／GLONASS组合单点定位的数学模型

1．1 基本观测方程

对于一个测码单频的GPS／GLONASS接收机，卫星至接收机间的伪距可以表示为［3］

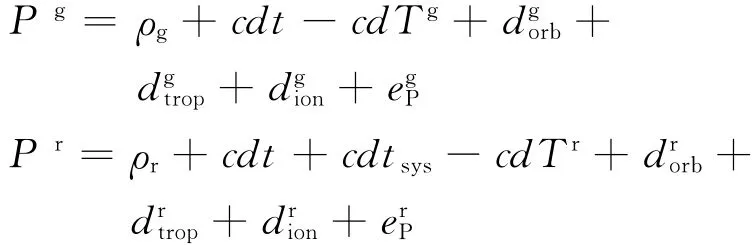
式中:g和r分别表示一颗GPS卫星和一颗GLONASS卫星；P为伪距观测值；ρ为卫星和接收机间的几何距离；c为光速；dt为接收机钟差；dT为卫星钟差；dtsys为GPS／GLONASS系统时间差；dorb为卫星轨道误差；dtrop为对流层延迟；dion为电离层延迟；e是观测噪声。

在上述观测方程中，电离层延迟采用克罗布歇（Klobuchar）模型改正，对流层延迟采用EGNOS模型进行改正，卫星位置和卫星钟差采用广播星历计算。对运用广播星历计算GLONASS卫星位置做较详细的介绍。

1．2 广播星历计算卫星位置

在GPS伪距单点定位的基础上，实现GPS／GLONASS组合导航单点定位。对GLONASS广播星历运用四阶龙格库塔（Runge－Kutta）数值积分方法，利用一种新的不需要进行轨道拟合的编程方法计算卫星位置［4］。

GLONASS广播星历不同于GPS，GPS广播星历给出的是开普勒轨道根数，每隔2h广播一次，通过给定一个时刻t，就可以通过导航电文参考时刻的开普勒轨道根数直接计算出卫星的位置，而GLONASS是PZ－90坐标系下参考时刻的卫星运动状态向量，每隔半个小时广播一次，如需要得到某个时间的卫星位置，就必须通过Runge－Kutta数值积分方法进行计算，再通过契贝雪夫（Chebyshev）插值的方法解算出卫星的位置，采用不需要插值的新算法。

在地固系中，卫星的运动方程见参考文献［5］，为一个二阶常微分方程组，且为隐函数，方程组中不含有自变量t，所以需要将方程组写成函数的形式

从而式（1）可化为一个一阶常微分方程组。

根据四阶Runge－Kutta算法计算GLONASS卫星位置，其详细推导微分方程组合积分公式见参考文献［6］。其中，取积分步长为30s，将积分公式依次循环计算，积分的次数和取得步长以及积分的时间有关系:n＝ （tb－t0）／h，得到tb时刻卫星的坐标。在实际计算过程中，由于n一般不是整数，以h定步长积分往往不能恰好得到tb时刻，采用新的计算方法，不需要进行拟合，就可以算出卫星位置。先以步长为h进行n次，积分到t0＋n·h时刻，最后一步将积分步长改为h＝tb－t0－n·h进行积分，得到所需要的tb时刻的卫星位置坐标［4］。

2 组合单点定位关键问题

进行组合单点定位时，GLONASS与GPS的坐标系统、时间系统和星历计算方法方面均不相同。

2．1 坐标系统转换

由于GLONASS坐标系统是PZ－90，而GPS的坐标系统是 WGS－84坐标系统，所以在进行数据融合时，必须进行相应的坐标转换。PZ－90和WGS－84坐标系之间的转换，通常采用布尔萨（Bursa）七参数模型，采用的形式为

2．2 时间系统转换

GLONASS采用的时间系统是前苏联的（UTC（SU））时（含有跳秒改正），而 GPS采用的是GPS时，没有跳秒改正，所以，在GPS／GLONASS组合定位时需要进行必要的时间转换。其GLONASST与GPST之间的关系为［8］

GLONASST≈GPST＋3h－ts

式中ts是跳秒，由导航电文给出。

但实际得到的GLONASS星历文件中，所采用的时间系统并非是GLONASST而是UTC，因此，在组合定位的数据处理中，二者只相差一个整数的跳秒。

3 算例分析

为了评价GPS／GLONASS组合单点定位的精度，选用IGS跟踪站BJFS在2011年8月28日一天中的2 880个历元观测数据。该站装备了双频双系统接收机TRIMBLE NETR8，能同时接收GPS和GLONASS卫星的观测数据。观测数据的采样间隔为30s，截止高度角为15°．利用 MATLAB编写的程序对该站C／A码伪距观测值进行组合单点定位，计算结果与ITRF提供的跟踪站坐标进行比较，计算出位置差异并转换至测站坐标E、N、U 3个方向。表1和表2示出了GPS／GLONASS组合单点定位的坐标值分别与实际坐标值和算术平均坐标在E、N和U方向的差异。

表1 GPS／GLONASS组合单点定位的坐标值与实际坐标值在E、N和U方向的差异

表2 GPS／GLONASS组合单点定位的坐标值与算术平均坐标值在E、N和U方向的差异

在GPS／GLONASS组合单点定位中，涉及来自GPS和GLONASS两种不同系统的伪距观测数据，在数据处理中需要确定这两类观测的权。通过卫星的高度角来定权，并将GPS和GLONASS观测值的初始的权值设置为8∶1进行计算。基于单历元解算，采用最小二乘法计算各个历元的数据。

表1和表2表明:GPS／GLONASS组合单点定位的坐标值与实际坐标值和算术平均坐标值在E、N和U三个方向上的均方根（RMS）、最大值（Max）、平均值（Mean）要比GPS和GLONASS单系统定位的差异值要小，反映了组合定位的精度要优于单系统条件下的定位精度。而且GLONASS在E、N和U方向上RMS、Max、Mean值要明显大于GPS和GPS／GLONASS组合的值，但GPS在三个方向上的位置差异值与GPS／GLONASS组合的位置差异值比较接近，稍微比组合的位置差异值要大一点，从而体现了组合定位可以提高定位精度的目的，实现了组合导航定位的现实意义。

为了更直观的表现GPS、GLONASS和GPS／GLONASS组合单点定位的坐标值与实际坐标值和算术平均坐标在E、N和U方向位置差异，将位置差异曲线图分别绘制如下，如图1和图2所示。

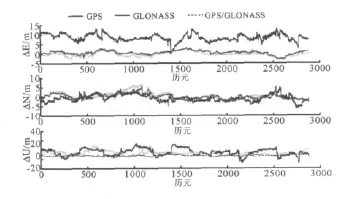
图1 GPS、GLONASS和GPS／GLONASS组合单点定位的坐标值与实际坐标值在E、N和U方向位置差异曲线

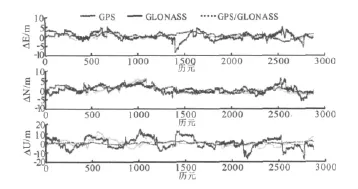
图2 GPS、GLONASS和GPS／GLONASS组合单点定位的坐标值与算术平均坐标值在E、N和U方向位置差异曲线

从图1和图2中可以较为直观的看出在E、N和U三个方向上，GPS／GLONASS组合定位的位置差异值总体上要比GLONASS和GPS单系统条件下的位置差异值要小，而且GLONASS的位置差异曲线在零附近的变化幅度比较大，其最大位置偏差值超过10m，GPS和GPS／GLONASS组合的位置差异值在零附近的偏差值相对要小一些。从总体来看，GPS／GLONASS组合单点定位坐标值要好于GPS和GLONASS单独定位的坐标值。

由上述图表，组合定位坐标值与实际坐标值和算术平均坐标值比较中，差异值要明显小于单系统条件下的坐标差异值，反映了组合定位精度相对优于单独定位的精度，其中定位精度分析结果如图3所示。

图3 GPS、GLONASS和GPS／GLONASS组合单点定位的GDOP值和PDOP值曲线

从图3中可知，GPS和GLONASS的GDOP和PDOP值，都在1至5附近变化，而且GLONASS的GDOP和PDOP值的振幅要明显比GPS和GPS／GLONASS组合值要偏大。GPS／GLONASS组合单点定位的GDOP和PDOP值的均值在0．5附近，可以看出组合单点定位的精度的确要优于GPS和GLONASS的定位精度。

GPS和GLONASS的联合定位不仅可以改善GDOP和PDOP值，而且还可以较大限度的增加卫星的颗数，图4示出了在组合定位和非组合定位时各历元可观测卫星的颗数分布。

图4 GPS、GLONASS和GPS／GLONASS组合单点定位在不同的历元卫星颗数分布

从图4中可知单系统的GPS和GLONASS可观测卫星颗数都在10颗左右，由于GLONASS的卫星未完全发射，其卫星颗数要相对少于GPS的卫星颗数。但是，当GPS和GLONASS进行联合单点定位时，其卫星颗数有较为明显的增加，大致都在20颗左右。由于卫星系统测量定位的正确性极大地依赖定位计算中所用到的卫星数，而且用户对高效率和高精度的需求尤为迫切［9］，所以卫星颗数的增加，对于定位精度的提高有着重要的意义。

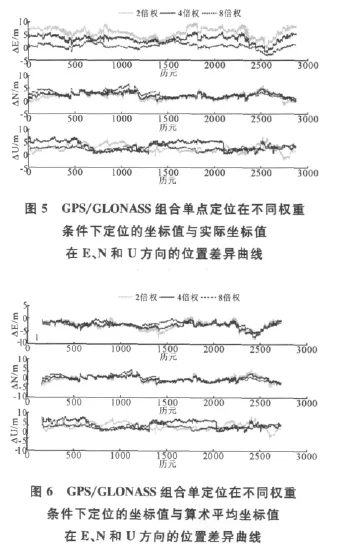
GPS和GLONASS组合定位需要考虑权重对于组合定位的影响，图5和图6分别为GPS／GLONASS组合定位在2倍、4倍和8倍权重条件下的坐标值与实际坐标和算术平均坐标在E、N和U方向的位置差异曲线图。

从图5和图6可以看出，不同权重的选择对于GPS／GLONASS组合单点定位的坐标值与实际坐标值和算术平均坐标值在E、N和U三个方向上的位置差异的影响不同。选择8倍权的三个方向上的位置差异值要相对小于选择2倍权和4倍权的差异值，得出选择合适权重可以适当提高组合定位精度的结论。

4 结 论

利用IGS跟踪站BJFS的观测数据和由ITRF提供该跟踪站的实际坐标对GPS／GLONASS组合单点定位进行处理，并与GPS和GLONASS单点定位的结果进行了比较分析，得到的组合导航定位精度要优于单系统定位精度。通过比较不同权重条件下GPS／GLONASS导航定位精度，得出了权重的选择对定位精度有一定的影响。分析了GPS、GLONASS和GPS／GLONASS组合单点定位的精度因子GDOP值和PDOP值，得出了组合单点定位的GDOP值和PDOP值要明显小于单系统条件下的值，体现组合定位的精度要优于非组合的定位精度。采用GPS／GLONASS组合单点定位时，卫星颗数也有了较大的增加，完全可以满足广播星历的单点定位的卫星颗数的要求。综上所述，GPS／GLONASS组合导航对于定位精度的提高具有重要的意义。

［1］ VASILY E，LVAN P，VALERY B．Glonass busi－ness prospects［J］．GPS WORLD，2008（3）:12－15．

［2］ 葛茂荣，过静珺，葛胜杰．GLONASS卫星坐标的计算方法［J］．测绘通报，1999（2）:2－4．

［3］ 蔡昌盛，戴吾蛟，匡翠林，等 ．单频GPS／GLONASS组合单点定位的精度评估［J］．大地测量与地球动力学，2011，31（3）:85－89．

［4］ 葛 奎，王解先．GLONASS卫星位置计算与程序实现［J］．测绘与空间地理信息，2009，32（2）:137－140．

［5］ 杨 剑，王泽明，孟 泱，等．GLONASS卫星轨道积分算法分析［J］．武汉大学学报·信息科学版，2006，31（7）:613－615．

［6］ 李建文．GLONASS卫星导航系统及 GPS／GLONASS组合应用研究［D］．郑州:信息工程大学，2001．

［7］ 杨 铮，党亚民，成英燕．GPS／GLONASS定位系统融合的坐标转换研究［J］．测绘科学，2008，33（2）:45－47．

［8］ 李 智，张若禹．GPS／GLONASS组合导航中的星历计算与数据融合［J］．指挥技术学院学报，1999，10（6）:19－22．

［9］ WILLIAM M，JONATHAN L．GPS＋GLONASS组合测量［J］．测绘通报，1999（6）:41－43．