GPS/伪卫星组合选址优化的一种思路*
2012-10-10李继尚刘常全郭颖斐王少宁倪维洋
李继尚,刘常全,郭颖斐,王少宁,倪维洋
(中国矿业大学环境与测绘学院,江苏 徐州221116)
0 引 言
伪卫星类似于地面GPS卫星,采用的导航电文格式与GPS基本一致,伪卫星可根据工程实际需要安装在选定的位置,现有的接收机可以同时接收来自GPS和伪卫星的信号[1]。利用伪卫星可有效增加可见星数目,有效改善卫星分布的几何图形结构,从而提高导航定位性能。
伪卫星加入的位置及个数目前主要是通过设计仿真程序或基于经验进行选定:通过给定若干备选方案(不同的伪卫星个数、方位角、高度角),进行仿真实验比较,选取定位精度因子(DOP)值最小的方案;基于一定的经验,通过样本比较,得到相对较优的布设方案[2]。通常采用的方法有网格法和蚁群搜索算法[3]。针对不同的工程需求,伪卫星布设数目不同,鉴于此,提出一种伪卫星选址优化的新思路:建立以观测时间、高度角、方位角为自变量,DOP值为因变量的三维全景模型,对观测时段内任意时刻的精度进行全时空显示,从而为伪卫星选址工作提供了依据。
1 理论分析
1.1 观测方程
伪卫星是设置在地面上、发射类似GPS信号的卫星,根据GPS伪距定位原理[4],伪卫星伪距观测方程为
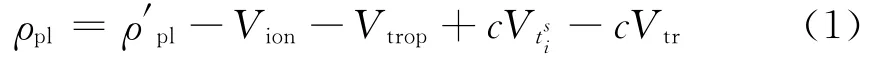
式中:ρpl为伪卫星的伪距观测值;ρ′pl为伪卫星与接收机之间几何距离;c为光速(取299 792 458 m/s);cVtsi、cVtr、Vion和Vtrop分别为卫星钟差、接收机的钟差、多路径误差和对流层误差,GPS伪距观测方程为
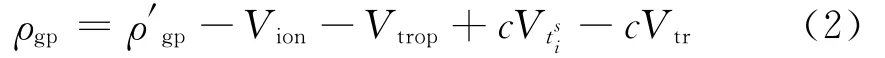
式中:ρgp为GPS伪距观测值;ρ′gp为测站与卫星之间几何距离;c为光速(取 299 792 458m/s);cVtsi、cVtr、Vion和Vtrop分别为卫星钟差、接收机钟差、电离层误差和对流层误差。
伪卫星与GPS的观测方程在形式上类似,但伪卫星的主要误差源区别于GPS,伪卫星发射器布设在地面高度角较小的位置,信号不经过电离层,观测值无电离层改正,其多路径影响看做常量[5]。
1.2 精度因子
如果接收机钟差作为一个未知数,卫星钟差可以从导航电文中取得,电离层延迟误差和对流层延迟误差按一定模型计算得到;则共有四个未知数,待测点坐标和接收机钟差,列出某一历元时间的观测方程:

设(X0,Y0,Z0),(δx,δy,δz)分别为观测站坐标的近似值与改正数,将伪距观测方程进行泰勒展开并令

简化为Aiδx+Li=0,误差方程式为

未知参数的协因数阵在空间直角坐标中的一般形式为
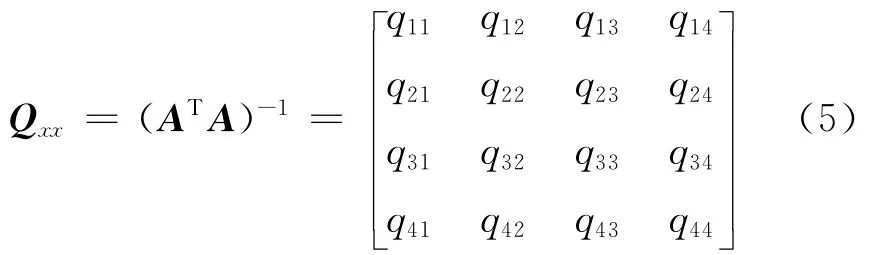
根据需要需提高某方向上的定位精度故常采用其在大地坐标系中的表达形式来估算测站点的位置精度,依据方差与协方差传播定律可得:

R为旋转矩阵;α、β分别为测站经纬度。
则t时刻:
绝对定位几何精度因子:

2 露天矿区GPS伪卫星组合应用仿真
2.1 仿真实验
为了分析可视卫星数不足,加入伪卫星后对定位精度的影响,仿真实验中伪卫星布设在方位角分别在30°,90°,240°,150°,225°的位置上,采用PDOP值作为评价指标。选取了1 000个连续历元,用Matlab[5]模拟某露天矿区卫星遮挡情况,绘制出不同伪卫星布设方案下的PDOP值,如图1所示。
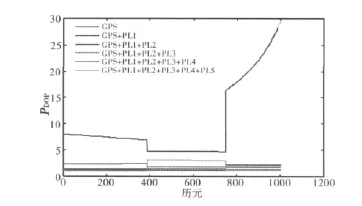
图1 不同方案的比较
2.2 实验结果分析
分析加入不同数量的伪卫星PDOP值的变化情况,可以看出:
1)加入伪卫星后DOP值的整体趋势是降低的,加入一颗精度得到明显提高,随着更多伪卫星加入,精度提高不明显。
2)PL5加入后PDOP并没有多大改善,在380至750历元反而影响PDOP值,出于投资不考虑加入PL5伪卫星。
3 伪卫星优化设计模型
为了获得伪卫星选址的最优解,建立基于时间、高度角、方位角为自变量[2]的三维选址全景优化模型,对于给定测站位置,其PDOP仅受伪卫星(卫星)与测站相对位置的影响,即卫星的方位角a,高度角h,以及时间t,故建立以(a,h,t)为自变量,PDOP为因变量的三维剖面模型

式中:a∈ [0°,360°],h∈ [-90°,-90°];t>0.
3.1 技术路线
模型的基本思路:依照选定的时间间隔截取不同方位角、高度角下PDOP的剖面图,直观给出最优区域,并结合现场布设环境,加权判断最优解,若不是则重新选择区域,布设流程图如图2所示。
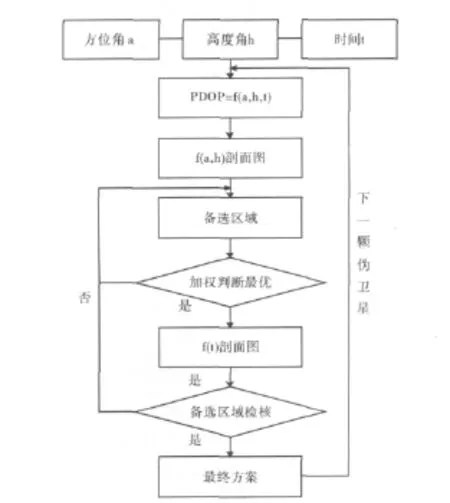
图2 伪卫星布设流程图
3.2 实验分析
实验采用天宝接收机接收的实测数据,数据采集频率为1Hz,取600历元处,以设站点为中心,高度角为[-90°,90°],方位角为[0°,360°]进行伪卫星的布设[6],分析加入伪卫星后定位精度的变化。剖面图如图3所示。
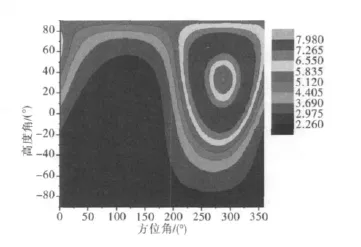
图3 布设一颗伪卫星时不同位置的PDOP值
4 结 论
针对露天矿区GPS定位中存在的困难,利用GPS/伪卫星的组合方法来提高定位精度,仿真实验证明:加入一定数量和方位角的伪卫星可以提高定位精度;随着伪卫星数量的增加,其精度因子值进一步减小,但伪卫星的数目受制于投资成本。针对伪卫星的位置最优选择的问题,提出了三维全景模型:沿时间轴截取PDOP的剖面,依据PDOP值选取较优区域作为备选,同时结合现场环境选择最优位置,选出第一颗最优伪卫星之后,再加入第二颗伪卫星,重复以上的步骤。该方法直观、有效,为伪卫星选址提供了新思路。
[1] 何秀凤.变形监测新方法及其应用[M].北京:科学出版社,2007.
[2] 刘 超,高井祥,于子晏,等.GPS/伪卫星相对定位中伪卫星优化布设模型研究[J].中国矿业大学学报,2012,41(1):120-126.
[3] 陈 烨.用于连续函数优化的蚁群算法[J].四川大学学报·工程科学版,2004,36(6):117-120.
[4] 周忠谟,易杰军,周 琪.GPS卫星测量原理与应用[M].北京:测绘出版社,1997:119-120.
[5] 朱习军.MATLAB数值分析与应用[M].北京:电子工业出版社,2009.
[6] 姜 昆,王 坚,刘 超.GNSS/Pseudolites导航定位中的伪卫星优化模型研究[J].大地测量与地球动力学,2012,32(2):134-138.
