基于容错型联邦强跟踪滤波的多星座组合导航算法研究*
2012-10-10张国柱雍少为
张 辉,吴 鹏,张国柱,雍少为
(1.国防科学技术大学电子科学与工程学院卫星导航研发中心,湖南 长沙410073;2.61081部队,北京100094)
0 引 言
目前,已有北斗系统(COMPASS)、GPS和GLONASS三个全球导航系统能够提供导航定位服务。但是,即便是目前最成熟的卫星导航系统GPS也存在一些缺陷。例如,在航空领域,飞行器经常工作在高动态环境下,而且对导航定位系统的精度和可靠性要求也较高,GPS不能满足作为单一导航系统的要求[1]。多星座组合导航定位具有可用卫星数量多、覆盖性好、定位精度高、可靠性高等优点,正逐步成为卫星导航领域的研究热点之一。
多星座组合导航系统信息处理多采用的方法有集中式融合和分布式融合。由于集中式融合方案存在实时计算困难、容错性能较差的问题,因此,大多采用分布式融合[2],其中最著名的就是由Carlson提出的联邦滤波算法[3]。
文献[4]将GPS、GLONASS和GALILEO三系统视为三个联邦成员,构成针对GNSS系统的联邦滤波器,仿真结果表明:定位精度在一定程度上得到提高。但是,常规联邦滤波器中的子滤波器为扩展卡尔曼滤波器(EKF),它是建立在H2估计准则基础上的,要求准确已知系统模型和噪声统计特性[5],而且在系统达到稳定状态下,将丧失对突变系统状态的跟踪能力[6-7],这在实际应用中带来很大局限性。针对这一问题,文献[8]提出了一种基于卡尔曼滤波的多星座组合导航双重自适应联合滤波算法,具有较好的机动目标跟踪能力,提高了多星座组合导航系统的定位精度和可靠性。但由于“当前”统计模型中的系统加速度参数amax和a-max在跟踪过程中不能自适应,使得系统方差的调整有限,对于机动加速度大范围变动或突变的目标,其状态跟踪的快速性和精度的协调很难令人满意[9]。另外,由于采用了重置-融合联邦滤波结构,容错性能较差。
针对EKF的缺陷,周东华等在文献[10]中提出了著名的强跟踪滤波器(STF)。STF与通常的滤波器相比有以下优良特性:(1)较强的关于模型参数失配的鲁棒性;(2)较低的关于噪声及初值统计特性的敏感性;(3)极强的关于突变状态的跟踪能力,并在滤波器达到稳态时仍保持这种能力;(4)适中的计算复杂性。
主要研究载体在高动态环境下的多星座组合导航系统信息处理算法。此时,系统状态变化剧烈,动态噪声和观测噪声难以确定,同时,对导航定位的精度和可靠性要求较高。针对这一问题,在采用容错性能好、运算速度快的容错型联邦滤波器的基础上,改进子滤波器为强跟踪滤波器,增强了算法对模型误差的鲁棒性和对系统状态的跟踪能力。仿真结果证明:本算法优于传统的联邦滤波算法。
1 容错型联邦强跟踪滤波器结构设计
联邦滤波器主要分为四种基本结构:融合-重置式(FR)、零重置式(ZR)、无重置式(NR)和重调式(RS)等。它们的性能对比如表1所示。

表1 联邦滤波算法四种基本结构性能比较
NR结构联邦滤波较其他结构的联邦滤波有如下优势[11]:
1)容错性能强:各子滤波器独立工作,由于没有主滤波器到子滤波器的信息重置,避免了一个传感器故障造成各子滤波器交叉感染,容错性最好。
2)运算速度快:由于不需要重置,可以在子滤波器向主滤波器发送完状态估计值和方差后立即进行下一次运算,运算速度最快。
NR结构唯一不足是精度较FR结构稍有下降(但仍比任何一个子系统的精度高)。由于NR的特点,这种方案被认为是容错型联邦滤波结构(FTFF).
为同时发挥多星座组合导航系统精度和可靠性优势,加上导航系统的实时性运算要求,选用容错型联邦滤波器。如前所述,容错型联邦滤波器的子滤波器是扩展卡尔曼滤波器,存在着对模型误差的鲁棒性较差、对系统状态的跟踪性能不强的问题,不能满足高动态载体导航定位的要求。因此,采用强跟踪滤波器替换原来的子滤波器,构成容错型联邦强跟踪滤波器(FTFSTF),达到增强算法的鲁棒性和跟踪能力的目的。算法具体结构如图1所示。

图1 容错型联邦强跟踪滤波器结构
其中,全局算法采用容错型联邦滤波结构;各卫星导航系统对应的子滤波器设计为强跟踪滤波器,根据状态方程和量测方程进行滤波,输出建立在单一导航系统量测基础上的系统状态估计结果;各子系统配置实时的故障检测和隔离模块(FDI),检测正常的状态估计结果被送往主滤波器;主滤波器对接收到的各子滤波器估计结果进行最优融合,得到组合系统对系统状态的最终估计^Xg,Pg,且无对子滤波器的状态重置。
2 FTFSTF算法描述
2.1 系统模型建立
2.1.1 系统状态方程
由于各卫星导航系统的导航定位原理相同,因此,可以采用相同的系统模型。

式中:τx,τy,τz分别为加速度时间相关常数;τξ为钟漂的时间相关常数;sx(t),sy(t),sz(t),sξ(t)分别为(0,σ2x),(0,σ2y),(0,σ2z),(0,σ2ξ)的高斯白噪声。
离散化后的系统状态方程为

式中

同理可得Φy,Φz.

Wk的协方差为

2.1.2 系统观测方程
取观测量矩阵为
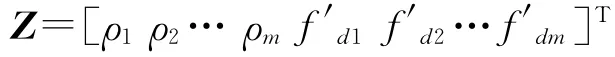
式中:ρi、f′di分别为伪距观测量和线性化的多普勒观测量;m为观测到的卫星数。计算公式为

式中:Vsi表示卫星i的当前速度;Vu表示用户当前速度;Ai=[hxihyihzi]为用户到卫星i的方向余弦矢量。
将上面两式合并在一起并离散化,则系统观测方程为

式中

式中:σ2iρ为卫星i的伪距观测方差;σ2if为卫星i的多普勒观测方差。需注意的是:由于COMPASS导航星座是由GEO、IGSO和MEO三种轨道类型的卫星组成,各种卫星的观测噪声是不同的。
2.2 子滤波器算法
子滤波器为强跟踪滤波器。强跟踪滤波器,通过在线选择增益Kk使得状态残差估计最小,且输出的残差序列保持处处正交,从而强迫滤波器保持对实际系统状态的跟踪。
考虑由式(2)与式(5)构成的非线性系统,在扩展卡尔曼滤波器的估计误差协方差阵中引入次优渐消矩阵,对不同数据通道进行渐消,使不同时刻的残差序列处处正交,则构成一种强跟踪滤波器—带多重次优渐消因子的扩展卡尔曼滤波器(SMFEKF)[10]。
SMFEKF的具体算法为

式中LMDk=diag{λ1,k,λ2,k,…,λn,k},λi,k≥1,i=1,2…n为对应状态变量的多重次优渐消矩阵。
考虑到导航系统的实时性运算要求,渐消矩阵采用适合在线运算的一步次优算法[10]。
若由系统先验信息可大致确定

则

式中:
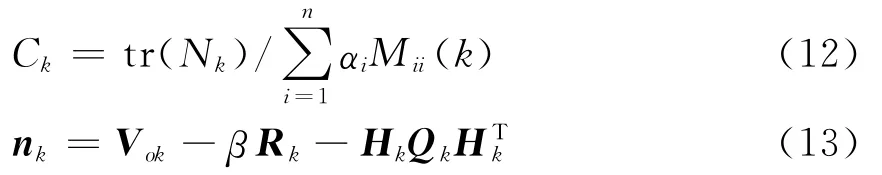
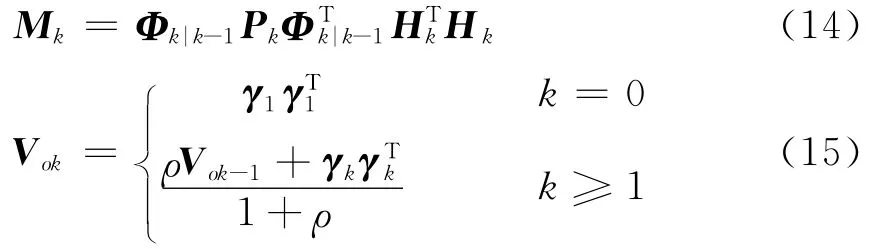
式中:0.95≤ρ≤0.995为遗忘因子;β为弱化因子,它的引入可以使状态估计更加平滑。β的取值可凭经验选定,也可通过仿真由下面准则确定[12]
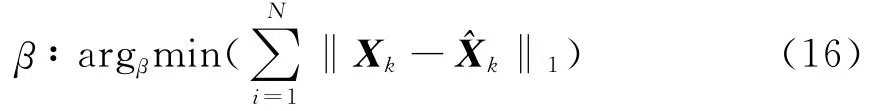
可以看出,当系统状态发生突变时,估计误差γkγTk的增大将引起误差方差阵Vok增大,相应的时变渐消因子λi,k增大,滤波器的跟踪能力增强。当LMDk为单位矩阵时,SMFEKF算法便退化为EKF算法。
2.3 故障检测与隔离
文献[13]给出一种适合组合导航系统故障检测和隔离的方法——残差χ2检验法,计算量小,实时性强,设计灵活。基本方法如下

故障判断准则为

式中:θik为故障检测函数;γik为残差;Aik为残差方差;TD为预设故障检验门限。
当主滤波器检测到子滤波器i发生故障后,可以很快的拒绝接纳它的信息,而融合剩余子滤波器的信息,得到系统的最优估计。
2.4 主滤波器信息融合
主滤波器按照下式将n个子滤波器的估计结果进行融合。

式中:Xik、Pik分别表示第i个子滤波器的估计值和方差;Xgk、Pgk分别表示全局最优估计和方差。
3 算法仿真及结果分析
仿真中,飞机的初始位置为北纬28.05°,东经112.78°,高度300m,初始速度100m/s,航向正东。仿真进行了500s.其中,前200s为水平匀速飞行,201s~380s经历了加速、快速盘旋上升、减速等快速强机动的飞行状态,最后进入水平匀速飞行,飞行轨迹如图2所示。滤波器滤波周期T=1 s.相关模型参数选取为:COMPASS系统中τx=τy=τz=60;σ2x=σ2y=σ2z=(4.0)2,τξ=0.1,σ2ξ=(15.0)2:GPS系统中τx=τy=τz=100,σ2x=σ2y=σ2z=(3.0)2,τξ=0.1,σ2ξ=(10.0)2;GLONASS系统中,τx=τy=τz=30,σ2x=σ2y=σ2z=(5.0)2,τξ=0.1,σ2ξ=(20.0)2.观测卫星高度截止角为10°,伪距观测误差和伪距等效误差分别选取为COMPASS:IGSO和MEO卫星取15m、15m,GEO卫星取20 m、20m;GPS:10m,10m;GLONASS:30m,30 m.多普勒观测误差和多普勒等效误差分别选取为 COMPASS:0.15m/s,0.15m/s;GPS:0.1m/s,0.1m/s;GLONASS:0.3m/s,0.3m/s.STF中:ρ=0.95,β=1.9,由于卫星导航系统中位置和速度是可直接观测量,其他误差无法直接观测,而速度状态相对于位置状态更容易发生“突变”,相应的赋予更大的渐消因子比例系数会更有助于对易变状态的跟踪,所以取

为了验证算法的有效性,设计了3组实验,分别对比分析了FTFSTF算法与常规联邦滤波算法在机动跟踪性能、滤波精度和容错性能等方面的优劣。常规联邦滤波器中,子滤波器为EKF,整体采用FR联邦滤波结构,标记为EKF+FR.FTFSTF子滤波器采用STF,整体采用NR联邦滤波结构,标记为STF+NR.

图2 飞行轨迹仿真
实验一:FTFSTF跟踪性能仿真分析
赋予位置误差为100m的状态初值,分别采用FTFSTF与常规联邦滤波算法对载体进行定位测速解算,仿真结果如图3、图4所示。
仿真结果表明:当赋予不准确的状态初值时,系统收敛到稳定状态(定位误差7m),常规联邦滤波器用了约98s,FTFSTF只用了8s,FTFSTF较常规联邦滤波器收敛速度有较大幅度的提高;当载体在处于一般机动状态时,FTFSTF与常规联邦滤波器性能相当;当载体进行快速机动时,FTFSTF体现出较强的跟踪性能,但滤波精度有所下降,而常规联邦滤波器则出现较大的估计误差。这验证了FTFSTF采用的强跟踪滤波算法具有较强的自适应性:对于导航系统而言,当载体处于常规机动状态或者稳定状态时,STF渐消矩阵取单位阵,退化为EKF;当载体处于强机动状态时,STF通过实时调整渐消矩阵使状态残差序列处处正交来保持对系统状态的强跟踪性能。
实验二:FTFSTF滤波精度仿真分析
主要分析FTFSTF采用的NR联邦滤波结构与FR联邦滤波结构在滤波精度上的差别。由于当载体处于常规机动状态或者稳定状态时,STF退化为EKF,所以,研究飞机前200s的匀速飞行阶段,进行FTFSTF与常规联邦滤波器的性能对比分析。同时,赋予位置误差为20m的状态初值。仿真结果如图5、图6和表2所示。其中,滤波精度用均方根误差(RMSE)来衡量。

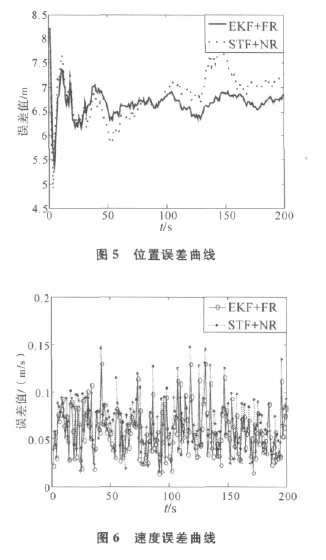
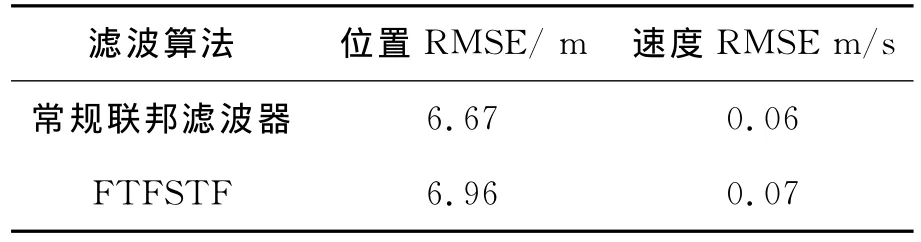
表2 常规联邦滤波器和FTFSTF滤波精度统计
结果表明:FTFSTF采用的NR联邦滤波结构较之FR联邦滤波结构滤波精度下降很小。
实验三:FTFSTF容错性能仿真分析
主要分析FTFSTF采用的NR结构相对FR结构在容错性能上的区别。假设GLONASS系统的2号星在80s~150s发生缓变故障,伪距中加入速率为0.5m/s的缓变误差,且FDI模块没有检测到这一故障,其他仿真条件同实验二,仿真结果如图7和图8所示。
仿真结果表明:GLONASS系统发生缓变故障时,由于常规联邦滤波器采用FR结构,导致各子滤波器发生交叉感染,整体滤波精度下降;而FTFSTF采用NR结构,不存在主滤波器到子滤波器的信息反馈,各子滤波器独立工作,彼此之间不存在耦合,保证了整体滤波精度,容错性能更好。

4 结 论
针对多星座组合导航在高动态场合应用的特点,提出了基于容错型联邦强跟踪滤波的多星座组合导航算法。通过对COMPASS/GPS/GLONASS组合导航系统建模仿真,验证了该算法的有效性。结果表明:该算法具有较强的容错性能和机动目标跟踪性能,能够有效提高多星座组合导航定位的精度和可靠性。由于采用了无重置联邦滤波结构和渐消矩阵的一步次优算法、残差χ2检验算法等实用算法,该算法具有计算量适中、容错性强、易于实现等优点,具有一定的工程实用价值。
但研究过程中发现,当载体做快速机动时,该算法的滤波精度有所下降。如何在保持强跟踪性能的同时,提高滤波精度需要更进一步研究。
[1] HEWITSON S ,WANG Jinling.GNSS receiver autonomous integrity monitoring(RAIM)performance analysis[J].GPS Solutions,2006,10(3):155-170.
[2] 张寅生,程洪玮,姚 静,等.组合导航卫星系统定位技术进展[J].全球定位系统,2009,34(5):1-6.
[3] CARLSON N A.Federated square filtering for decentralized parallel processes[J].IEEE Trans.Aerospace and Electronic Systems,1990,26(3):517-527.
[4] 初海彬.多种卫星导航定位系统共用关键技术研究[D].哈尔滨:哈尔滨工业大学,2004.
[5] 付梦印,邓志红,张继伟.Kalman滤波理论及其在导航系统中的应用[M].北京:科学出版社,2003.
[6] 周东华,叶银忠.现代故障诊断与容错控制[M].北京:清华大学出版社,2000.
[7] TERZIC B,JADRIC M.Design and implementation of the extend Kalman filter for the speed and motor position estimation of BLDC motor[J].IEEE Transactions on Industrial Electronics,2001,48(6):1065-1073.
[8] 吴 玲,孙永荣,陈传德.多星座组合导航自适应信息融合滤波算法[J].航天控制,2010,28(6):38-42.
[9] 刘建书,李厚人,刘云龙.基于“当前”统计模型的交互式多模型算法[J].系统工程与电子技术,2008,30(7):1351-1354.
[10] 周东华,席裕庚,张钟俊.一种带多重次优渐消因子的扩展卡尔曼滤波器[J].自动化学报,1991,17(6):689-695.
[11] 韩崇昭,朱洪艳,段战胜,等.多源信息融合[M].2版.北京:清华大学出版社,2010.
[12] BAI Mingli,ZHOU Donghua,SCHWARZ H.Identification of generalized friction for an experimental planar two-link flexible manipulator using strong tracking filter[J].IEEE Trans.on Robotics and Automation,1999,15(2):362-369.
[13] 秦永元,张洪钺,汪叔华.卡尔曼滤波与组合导航原理[M].西安:西北工业大学出版社,1998.
