基于AR模型的GPS精密卫星钟差建模与预报*
2012-10-10李长会闫国锋
李长会,刘 宁,李 森,闫国锋
(61365部队,天津300140)
0 引 言
GPS单点定位的精度受到许多误差的影响,如卫星轨道误差、卫星钟差、大气层延迟、接收机钟差及多路径效应[1]。在各类误差中,卫星钟差是影响定位精度的重要因素[2,3],目前,IGS的几个数据分析中心(GFZ,JPL等)可以提供GPS卫星的精密钟差,但是,这些钟差都是后处理结果。依据IGS的产品报告[4],IGS提供的卫星钟差的精度优于0.1ns,这种精度的卫星钟差,完全能够满足厘米级精度的定位要求,但是这类产品要13天后才能获取,不能满足实时单点定位的需求,而实时发布的广播钟差精度较低,不能满足实际应用的需要,因此,对精密钟差的预报进行研究很有必要。
最常用的卫星钟差预报模型有两种[5-7]:二次项模型和灰色模型。其中,二次项模型比较适合短周期预报,灰色模型比较适合长周期预报。两种方法虽然分别在长周期或短周期的预报中能取得良好的效果,但都仅仅是在研究了钟差的趋势项上建立的函数模型,并没有考虑钟差的随机模型。利用AR模型对提取钟差趋势项后的随机项进行建模,即在原有的钟差模型上加上随机补偿,从而使原有模型更加完善,计算了基于随机项建模的GPS精密卫星钟差预报的精度。
1 钟差预报模型
通常情况下,钟差是具有缓慢上升或下降趋势的数据,在短周期预测中,二次项拟合对于短期预测有先天的优势,其模型简单明了,易于编程实现。而对于钟差的长周期预测,由于星载原子钟对外界环境因素较为敏感,从而很难长期掌握并预测其复杂细致的变化规律,如果考虑将钟差的变化过程看作一个灰色系统,并用灰色模型[6]来进行预测,可以取得较好的结果,近些年来常用这种方法。
1.1 二次多项式拟合模型
二次多项式拟合模型就是将幂函数作为拟合函数,对时间间隔相等的卫星钟差时间序列数据进行拟合,并估计出参数a0,a1,a2

式中:T为卫星钟差;t为系统时间;a0、a1和a2分别为t0时刻原子钟相对于系统时间t的钟差、钟速和钟漂。
设卫星钟差为xi,观测误差为vi,则根据式(1)建立误差方程
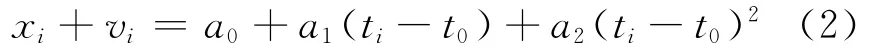
采用 最 小 二 乘 参 数 估 计,设^a0、^a1、^a2为 卫 星 参 数a0、a1、a2的最小二乘估值,记
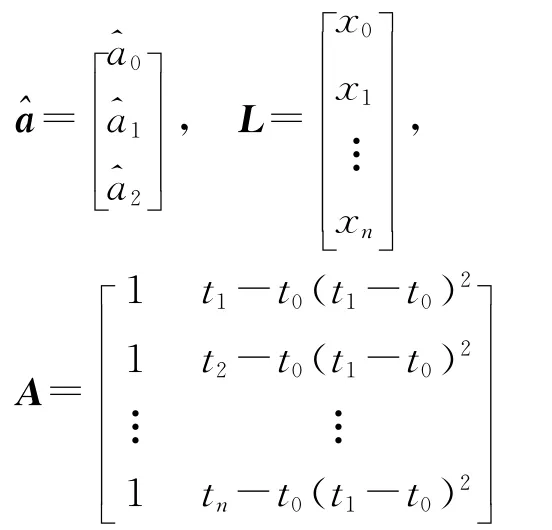
由最小二乘法原理可得估计值为

可得到二次项拟合模型为
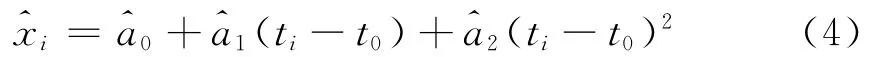
用上述模型可以进行钟差的短周期预测。
1.2 灰色模型
灰色模型是指部分信息已知、部分信息未知的系统,已知的信息称为白色,未知的信息称为黑色。用灰色模型做钟差预测时,通过对原始数据实行累加或累减使之成为具有较强规律的新数列,对此生成数列进行建模。由于星载原子钟对外界的干扰相当敏感,很难了解其内在的变化规律,因此,可以把钟差的变化过程看作是灰色系统。用灰色模型进行钟差预测,就是用指数函数来对时间间隔相等的钟差时间序列进行拟合,并通过对原始钟差数据实行累加或累减使之成为具有较强规律的新数列,对此生成数列进行建模。其具体过程为
设 X(0)= {X(0)(i),i=1,2,…,n}为原始钟差数据列,对X(0)进行一次累加生成一次累加序列

式(5)为 GM(1,1)模型,其解为
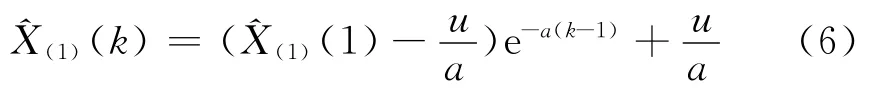
则预测值

式中:k为时间序列;a称为发展灰数;u称为控制灰数。
记参数 序 列 为^a,^a = [a,u]T,A 为 数 据 阵,L为数据列。
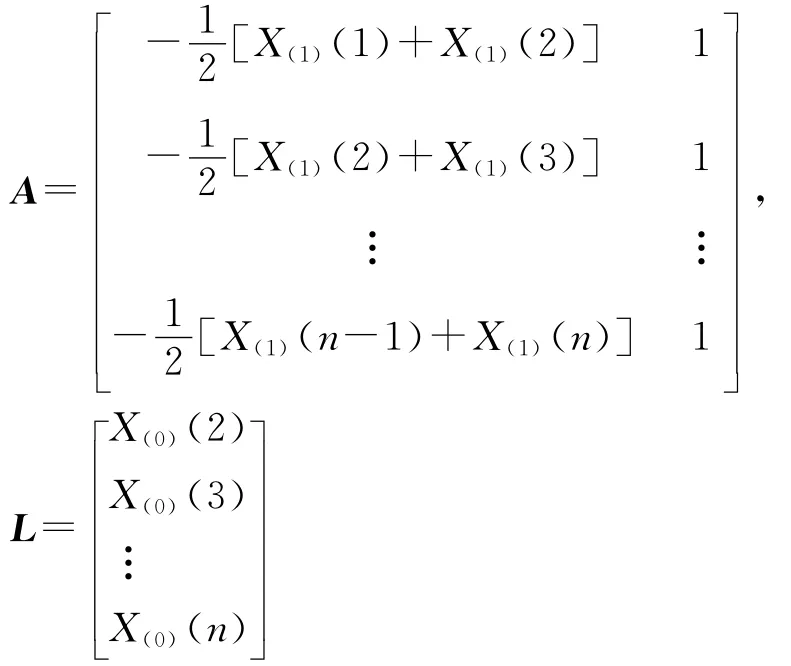
根据最小二乘法原理,^a可用下式求解

在估计出参数以后,可以用以上的灰色模型进行钟差预测。
2 提取趋势项后的随机项建模
在钟差模型建立之后,可以将上述模型看作是钟差模型的趋势项,在提取趋势项后,剩余的部分就是随机项。如果把随机项看作是平稳序列,由于钟差的时间相关性,可以对其随机项用AR模型来进行建模。
2.1 随机项模型的定阶
通过AR模型对随机项进行建模,必须进行模型的定阶。设{Yi}是钟差预测模型的随机项,采用AIC准则来进行定阶。虽然AIC准则通常会对阶数略有高估,但在预测问题中有利于多用数据,所以在实际计算中,AIC准则得到较为广泛应用。
AIC定阶准则:假定阶数p的上界为P0,当AR模型的阶数为k时,可以计算出相应模型的白噪声方差估计^σ2k,引入AIC函数

AIC(k)的最小值点^p称为AR模型的AIC定阶。
在阶数p=^p确定以后,对于AR(^p)模型即

式中t≥0,εt为高斯白噪声。
2.2 随机项模型的参数估计
在定阶完成后,需要对模型进行参数估计,对AR模型进行Yule Walker估计。Yule Walker估计不但具有计算简便的优点,而且这种估计方法是强相合估计。
用样 本 {x1,x2,…,xN}去 估 计 参 数 (^a1,^a2,…,^ap)T和^σ2.样本的Yule Walker方程如下

以及

在实际计算中,对钟差的随机项数据{x1,x2,…,xN}做零值化处理:

可构建样本的自协方差矩阵估计为

由上述公式可以得到AR模型的参数估计(^a1,^a2,…,^ap)T,至此,钟差预 测的随 机项模 型已经建立,可以把它当成随机改正加入到传统的钟差预测函数模型,以提高预测精度。
3 算例分析
为了验证所建模型的正确性和有效性,现用实例加以分析。采用从IGS官方网站上下载的钟差产品(igs****.clk_30s文件),从中选取9颗卫星数据进行分析。按照预测周期的长短,以及采用方法的不同,设计以下四种方案进行钟差预报。
1)在短周期预报中,通过二次多项式拟合的方法,用前一天钟差数据预报后一天的钟差;
2)在短周期预报中,通过基于随机项建模的二次多项式拟合方法,用前一天钟差数据预报后一天的钟差;
3)在长周期预报中,通过灰色模型预测方法,用前一天钟差数据预报后七天的钟差;
4)在长周期预报中,通过基于随机项建模的灰色模型预测方法,用前一天钟差数据预报后七天的钟差。
通过以上四种方案进行钟差预报,选取PRN编号为20的卫星的预报结果进行绘图分析,结果如图1~图4所示。
为验证模型的普适性,对9颗卫星的钟差做了上述四种方案的预报,用RMS描述其精度,并对所有9颗卫星进行计算统计,分别用表1和图5表示。


由计算结果可以看出:
1)比较图1与图2、图3与图4可以看出,在钟差短周期预报中,方案2的精度较方案1有所提高,即用二次项拟合提取趋势项后,再用时间序列分析法对随机项进行补偿可得到比较合适的模型。在钟差的长周期预报中,方案4的精度较方案3也有提高,用灰色模型提取趋势项后,再用时间序列分析法对随机项进行补偿可建立较好的预测模型。

表1 几种方案RMS误差比较
2)由图5与表1可以看出,不同的卫星钟,用同样的钟差预测方法得到的精度有非常明显的差异。由图5知,第3颗与第9颗卫星比其他6颗卫星的精度低很多,主要是由于第3颗与第9颗卫星上搭载的是铯钟,而其他6颗卫星上搭载的是铷钟。
3)短周期钟差预报的精度(方案1,方案2)要高于长周期预报的精度(方案3,方案4)。无论是钟差的短周期预报还是长周期预报,在随机项建模之后,加入随机补偿,都可有效提高钟差预报的精度。
4 结 论
在钟差的短周期预报和长周期预报中,通过二次项拟合或灰色模型建立钟差的趋势项模型,再对其随机项利用ARMA模型进行建模,这种方法同时考虑了钟差时间序列趋势项和随机项,可有效提高钟差预报的精度,并使原有模型更加完善。
[1] 韩保民.精密卫星钟差加密方法及其对星载GPS低轨卫星定轨精度影响[J].武汉大学学报,2006,31(12):1075-1077.
[2] XU Guochang.GPS theory,algorithms and applications[M].Germany:Springer,2007:76-77.
[3] 刘基余.GPS卫星导航定位原理与方法[M].科学出版社,2003:375-379.
[4] SENIOR K.Report of the IGS clock products working group[C]//16th Meeting of the CCTF,1April 2004,BIPM.
[5] 崔先强,焦文海.灰色系统模型在钟差预报中的应用[J].武汉大学学报,2005(5):447-450.
[6] 郑作亚,陈永奇,卢秀山.灰色模型修正及其在实时GPS卫星钟差预报中的应用研究[J].天文学报,2008,49(3):307-319 .
