波节管管内氦气流动与传热的计算及分析

韩怀志，李炳熙，何玉荣

(哈尔滨工业大学 能源科学与工程学院，黑龙江 哈尔滨 150001)

0 引言

近些年，国内外对波纹管的研究越来越多，Vicente和Garcia[1]等通过实验研究了螺旋波纹管在不同普朗特数下传热特性和阻力特性的影响。Rozzi和 Massini[2]研究了牛顿流体和非牛顿流体在螺旋波纹管中的对流换热和摩擦损失。波节管是波纹管的一种，是一种特殊形状的缩放管，是以普通圆管为基管，通过液压成型的方式挤出一个个圆弧凸起，形成由弧形段和直管段交替变化组成的波节型通道，在1990年由中国的郎奎提出[3]，波节管通过波形内的扰动提高管内外流体紊流的脉动性，促进湍流度的增加，另外直线段起着“积累能量”的作用，是不可缺少的。这种高效换热管应用在很多行业，煤气站汽化、电厂首战、油田输油管道加热、储藏设备制冷、宾馆、居民楼供生活用水、海水热交换等。波节管近些年在国内开展得比较多，武汉工程大学的徐建民，胡郑重[4]对3种不同规格波节管进行了模拟，从微观上说明了波节管的强化传热机理。

目前，波节管通常是采用传统的k-ε方法进行数值模拟[5，6]，这种两方程模型采用各向通行的湍流粘度来计算湍流应力，难于考虑流线型弯曲、漩涡、旋转和张力快速变化等因素的影响。为了克服这些缺点，有必要直接对Reynolds方程中的湍流脉动应力建立微分方程式并进行求解[7]。雷诺应力模型 (Reynolds stress model) 简称RSM模型，RSM是RANS中制作最精细的模型。放弃等方性边界速度假设，RSM使得雷诺平均N-S方程封闭，解决了关于方程中的雷诺压力及耗散速率。由于RSM比单方程和双方程模型更加严格的考虑了流线型弯曲、漩涡、旋转和张力快速变化，它对于复杂流动有更高精度预测的潜力。本文应用RSM模型对氦气在波节管和光管管内的流动和传热进行了数值模拟研究，考察不同Re数和不同结构下波节管内的Nu数和f以及η的变化规律。

1 模型建立

1.1 物理模型

如图1所示。波节管强化换热元件的几何结构包括波距P，波峰半径R，波谷半径r，以及顶入深度H。整个管长为2 000 mm，由于整个管长的计算量过大，截取中间的充分发展段的200 mm进行数值模拟，圆管直径D=20 mm，大圆弧半径R=5 mm，顶入深度H=3 mm，本文研究了不同波距P以及不同波谷半径r的传热特性和阻力特性变化。

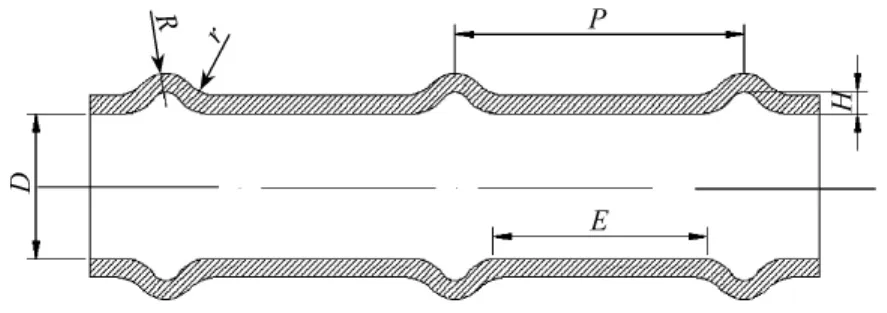
图1 波节管几何结构示意图Fig.1 The geometrical structure of corrugated tube

本模型应用ICEM软件对三维波节管结构进行网格划分，如图2所示。整个波节管皆采用规则的六面体网格，在直管处采用间距Δx=1 mm的网格，由于波形内流动和传热状态复杂，网格间距太大会导致结果发散，于是在波形内对网格进行加密，采用了间距Δx=0.5 mm的网格，可以保证结果收敛，而且避免了整个区域网格加密导致的计算量过大问题。考虑壁面对流换热和流动的影响，采用增强壁面处理，将壁面网格加密，根据不同流速调整壁面第一层网格的厚度，使 y+≈1，网格以1.3比率增长，直到和主流区网格间距相同。

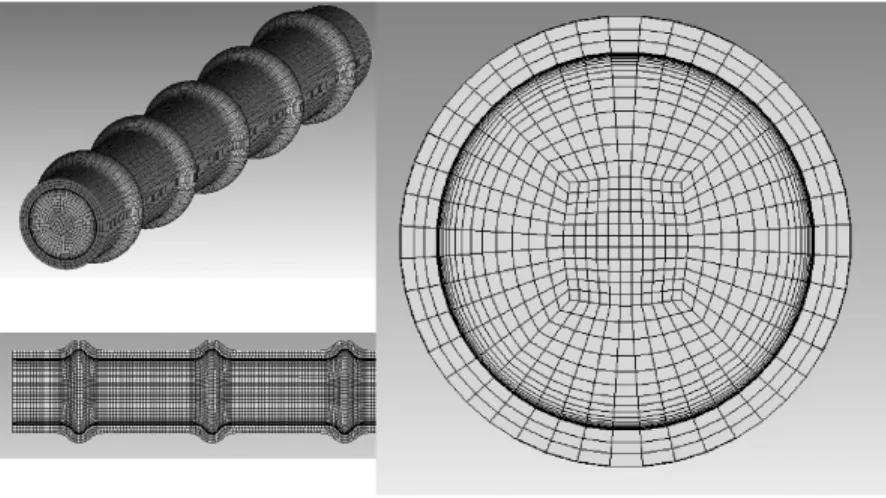
图2 三维波节管网格划分示意图Fig.2 Meshing of 3D corrugated tube

1.2 数值模型

本文采用RSM模型对波节管内流动和传热特性进行了数值模拟，根据波节管的运行特点作出以下合理假设:

(1)管内流体不可压缩且为充分发展的湍流流动;

(2)流体物性不发生变化且边界为无滑移流动;

(3)忽略重力影响。

则系统平均连续性方程、平均 Navier-Stokes动量方程和平均能量方程分别表示如下:

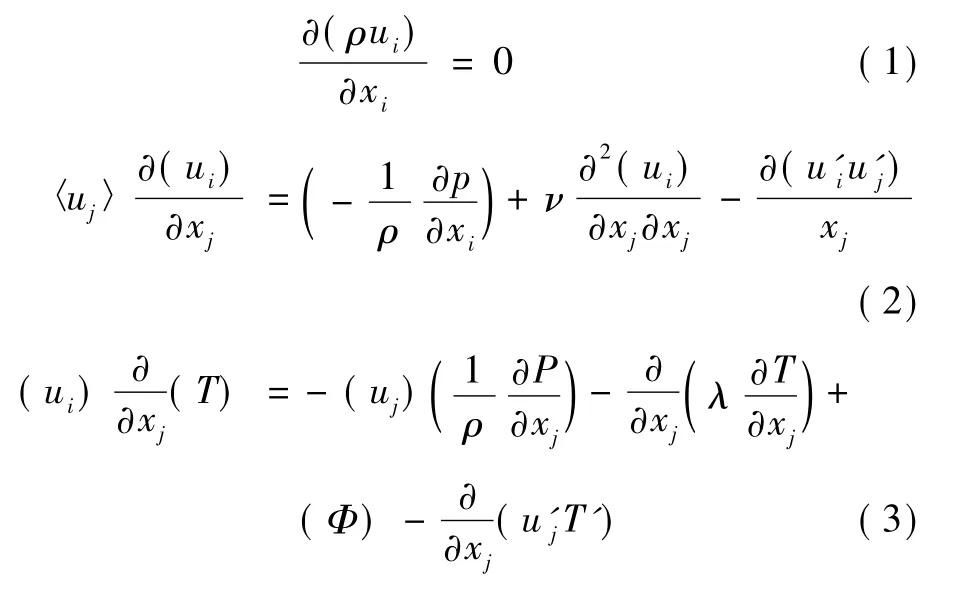
系统平均N-S方程称为雷诺平均方程，可以发现方程中除了平均力的作用，还有一项附加应力作用项，即雷诺应力项，正是由于雷诺应力的出现，导致雷诺方程不封闭。

RSM方法通过求解雷诺输运方程使方程封闭，雷诺输运方程如下:

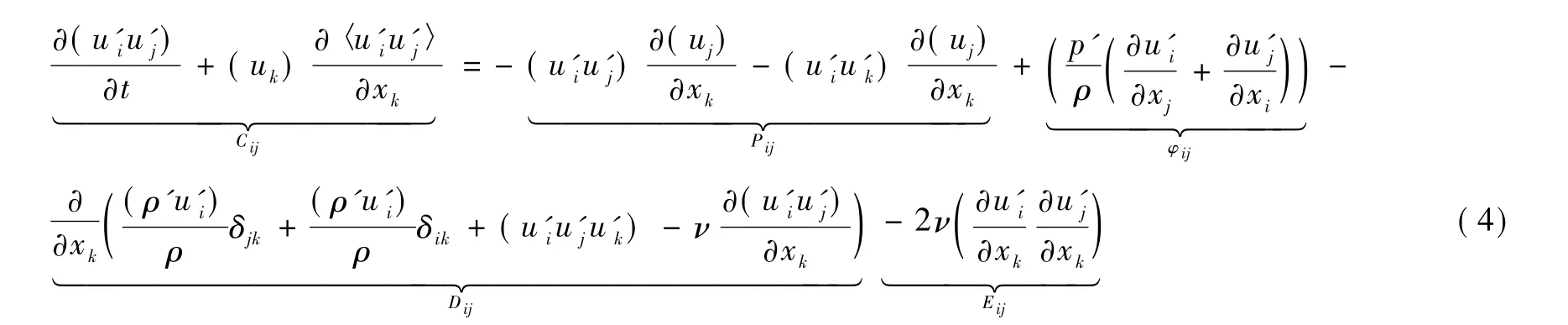
1.3 计算模型

本模型采用有限体积法离散方程，非耦合的稳态隐式格式求解。采用RSM湍流模型计算模拟管内湍流时的传热和流动情况。压力与速度的耦合计算采用SIMPLE方法，对流项采用一阶迎风格式，定义收敛的条件为， (u'u')残差绝对值小于10－4。进口和出口均采用充分发展边界条件，传热工质为氦气，相应的边界条件处理如下:

(1)入口条件:u=uin，v=w=0，T=Tin=663.15 K，入口湍流设定采用湍流强度I=5%和水力直径d=20 mm;

(2)出口条件:P=Po=3 MPa，出口湍流设定采用湍流强度I=5%和粘性比μtμ－1lam=5%;

(3)壁面边界条件:在管壁外壁面采用定壁温 tw=600 K，管内壁采用固体和流动耦合处理，管内壁为无滑移边界u=v=w=0。

2 计算结果及讨论

2.1 数据处理公式

换热管性能主要包括换热性能和阻力性能，换热性能主要由努谢尔特数Nu来表征:

式中:α为对流换热系数;D为特征长度;λ为导热系数。

阻力性能主要由摩擦阻力系数f来表征:

式中:ΔP为压力降;ub为平均速度;ρ为密度;D为管径;L为管长。

为了深入研究各种因素对强化换热效果的影响，引入综合传热因子η，其定义式为

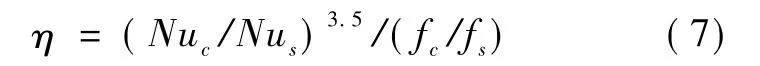
Nuc为波纹管努塞尔特数数;Nus为光管管努塞尔特数数;fc为波纹管摩擦因子;fs为光管摩擦因子。

2.2 强化机理分析

图3给出了波节管管内速度场矢量图，波节管中由于周期性波纹形状的存在，波节管各个波形内沿流动方向产生了一系列的旋涡，破坏了流动边界层，使流体主流区的掺混能力增强，从而达到管内强化换热的效果。

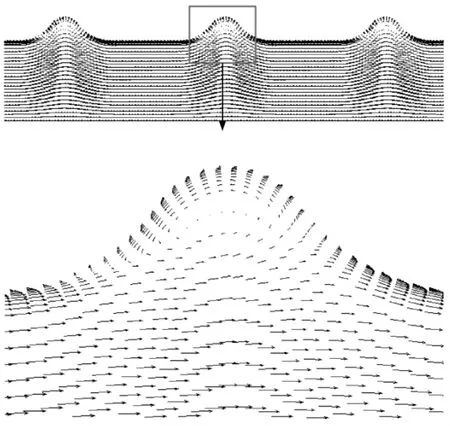
图3 波节管管内速度场矢量图Re=50 076Fig.3 Velocity vector field of tube side in the corrugated tuber，Re=50 076

图4给出了波节管管内温度场分布云图，波节管内波形的上游区域温度变化率较小，下游区域较大，说明下游区的热边界层厚度比上游区小，因此下游区的强化换热效果比上游明显。

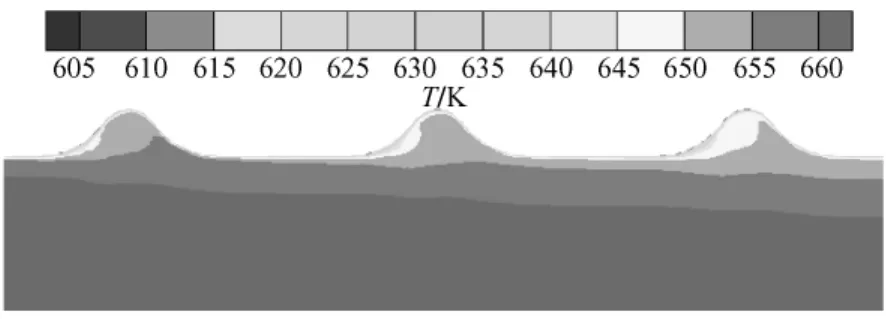
图4 波节管管内温度场分布云图Re=50 076Fig.4 Temperature field of tube side in the corrugated tube，Re=50 076

2.3 传热优化计算

图5给出了不同波距P中Nu数和随Re的变化，由图可知随着Re的增加，波节管和光管中的Nu数逐渐增加，并且波纹管比光管的增加速度快，不同波距Nu数增加速度几乎相同。随着波节管波距P的增加，Nu数逐渐减小。

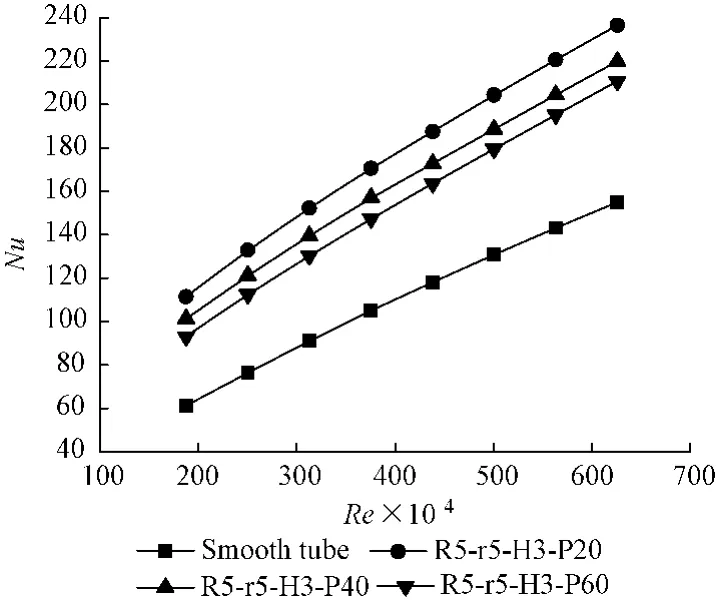
图5 不同波距P中Nu数随Re变化Fig.5 Nu along with Re in various pitch

图6给出了不同波距P中Nu数和随Re的变化，由图可知随着Re的增加，波节管和光管中的压力降ΔP逐渐增加，并且增加速度逐渐变快，波纹管比光管增加速度快，小波距比大波距的波节管增加速度快。随着波节管波距P的增加，ΔP逐渐减小。

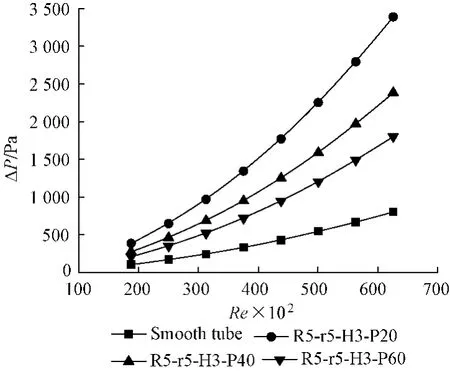
图6 不同波距P中ΔP随Re变化Fig.6 ΔP along with Re in various pitch

图7给出了不同波谷半径下Nuc/Nus随波距P的变化，Nuc/Nus是一个无量纲数，是波节管和光管Nu的比值。由图可知随着波距P的增加，Nuc/Nus逐渐减小，并且曲线的斜率先逐渐减小后逐渐增加，说明波节管相对光管的换热效果随着波距的增加是逐渐减小的，存在一个间距P=40 mm使换热效果降低率达到最小。随着波谷半径r的增加，Nuc/Nus先增加后减小，当r=5 mm时，波节管的换热效果较佳。

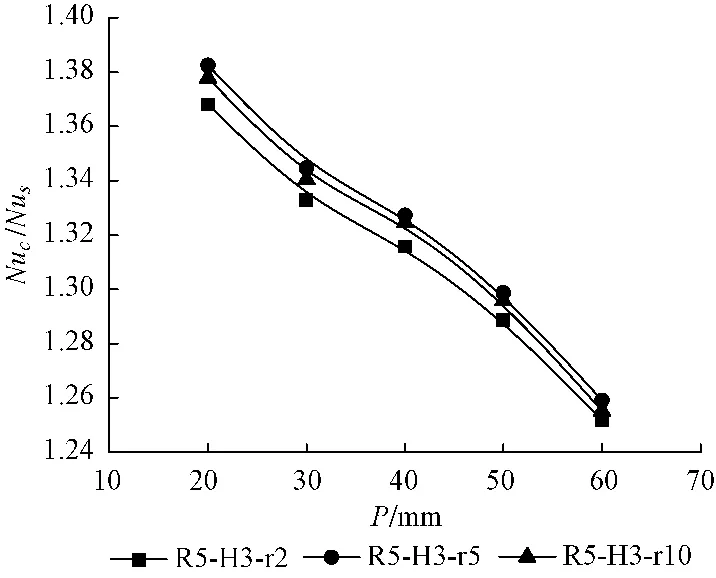
图7 不同波谷半径下Nuc/Nus随波距P变化Fig.7 Nu ratio along with Re in various wave tough radius

图8给出了不同波谷半径下ΔPc/ΔPs随波距P逐渐减小的变化，ΔPc/ΔPs是一个无量纲书，是波节管和光管ΔP的比值。由图可知随着波距P的增加，ΔPc/ΔPs逐渐减小，并且曲线斜率先逐渐减小，随后呈线性变化。说明波节管相对光管的阻力降是逐渐减小的，存在一个最小间距P=40 mm，使阻力降的减小率达到最低，在大于等于P时阻力降的减小率都相同。随着波谷半径r的增加，ΔPc/ΔPs是逐渐减小的。

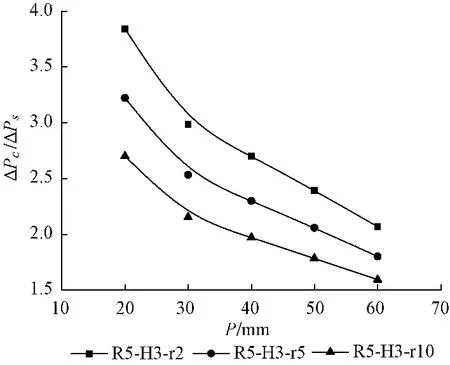
图8 不同波谷半径下ΔPc/ΔPs随波距P变化Fig.8 ΔP ratio along with Re in various wave tough radius

图9 不同波谷半径下η随Re数变化Fig.9 η along with Re in various wave tough radius

图9给出了不同波距P下η随Re数的变化，由图可知，随着雷诺数的增加，综合传热因子η逐渐减小，并且曲线斜率逐渐减小，说明η的降低率逐渐减小。不同波距下的η在较高雷诺数下差距明显，而随着雷诺数的降低，差距逐渐减小，当Re=20 000时，不同波距下的η相同，当Re＞20 000时，随着波距P的增加，综合传热因子逐渐增加，Re＜20 000时，随着波距 P的增加，综合传热因子逐渐减小。

图10给出了不同波谷半径下η随波距P的变化，由图可知，随着波距P的增加，综合传热因子η逐渐增加，并且曲线斜率逐渐减小，说明η的增加率逐渐减小。随着波谷半径r的增加，η逐渐增加。当r=5～10时，η在各个波距P下几乎均大于1，综合传热效果优于光管，当 r=2时，η在各个波距P下均小于1。

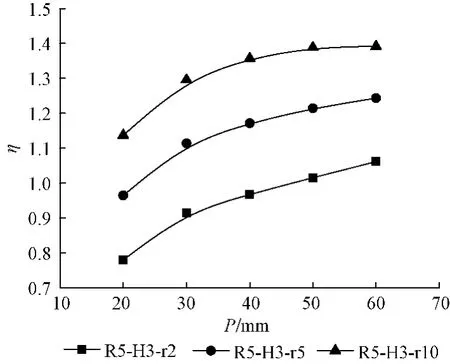
图10 不同波谷半径下η随波距P变化Fig.10 η along with Re in various wave tough radius

3 结论

(1)氦气在波节管中流动时，随着氦气雷诺数的增加，换热管传热性能和阻力降也逐渐增加，而综合传热效率却有所降低。

(2)波谷半径使氦气从波谷向波峰流动更加平滑，减小了上游区域的流动死区，使流动阻力降显著降低，波节管的综合传热效率明显提高。

(3)波距对波节管的换热性能，阻力降以及综合传热系数有重要影响。

[1]Vicente P G，Garcia A．Experimental investigation on heat transfer and frictional characteristics of spirally corrugated tubes in turbulent flow at different Prandtl number[J]．Heat and Mass Transfer，2004，(47):671 －681．

[2]Rozzi S，Massini R．Heat treatment of fluid foods in a shell and tube heat exchanger:Comparison between smooth and helically corrugated wall tubes[J]．Journal of Food Engineering，2007，(79):249－254．

[3]郎奎．波节管换热器的设计[J]．节能，1995，(6):38－41．

[4]徐建民，胡郑重．波纹管管内强化换热有限元Ansys分析[J]．石油化工设备，2007，36(1):4－7．

[5]徐建民，王晓清．波节管管内流动和传热的数值模拟[J]．石油化工设备，2008，37(1):4－7．

[6]曾敏，石磊，陶文铨．波纹管管内层流流动和换热规律的实验研究及数值模拟[J]．工程热物理学报，2006，27(1):142－144．

[7]Hoggs，Leschziner M A．Computation of highly swirling confined flow with a Reynolds stress turbulent model[J]．AIAA J，1989，27(1):57－63．