海杂波背景下的GRNN小目标检测

卢宁于才唐伟

(电子科技大学 成都 611731)

1 引言

海杂波［1］是指来自海洋表面雷达反射回波。在传统情况下，海杂波一直被认为是随机信号，并用统计模型来拟合，用统计判决理论来研究和处理。但是，海浪是一个自然存在的物体，有其存在的物理环境和形成海浪的力学结构，海浪的这些特性必定通过电磁波回波即海杂波反映出来。所以无论是基于高斯分布还是韦伯尔等分布建立的海杂波信号的统计模型，适用范围有限，都不能很好的反映海杂波本质。

S.Haykin［2］等人通过对精密测量的雷达海杂波数据反复研究，得出海杂波具有混沌特性［3，4］，具有实际的可预测性。

而基于GRNN(广义回归神经网络)具有良好的预测性和时速性等优点，可以先利用Takens嵌入式定理对海杂波相空间重构，再采用GRNN法进行目标检测，通过加拿大 McMaster大学采用的 IPIX雷达在Dartmouth地区海域实测数据［5］的验证，此方法确实可行，有良好的效果。GRNN小目标检测法总流程图如图1所示。

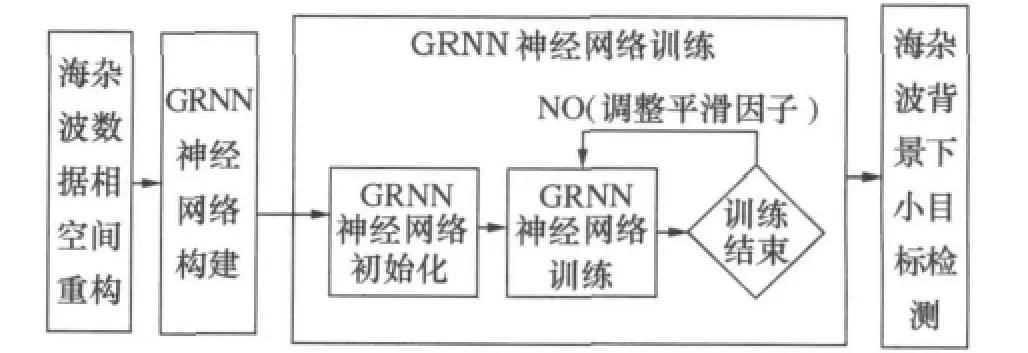
图1 GRNN小目标检测法总方案流程图

2 相空间重构模型

海杂波相空间重构目的是将一维时间序列重构到多维空间中以便于分析。

1981年，Takens提出了 Takens嵌入式定理从理论上证明了从单变量序列重构混沌奇异吸引子相空间的可行性。

由于数值微分是一个对误差相当敏感的计算问题，在此采用坐标延迟的相空间重构法，其本质是通过一维时间序列重构到m维相空间矢量:

式中:m为计算嵌入维数;τ为计算延迟时间。

坐标延迟相空间重构主要步骤［6］:

步骤一:计算嵌入维数m;采用G－P算法［7］提出相关维数。嵌入维数过低，会将空间中相隔很远的点投影成为邻近点，从而不能正确反映原系统的动力学特性，反之，重构相空间自由变量增加，会大大增加计算时间，浪费资源;

步骤二:计算延迟时间τ［8］;延迟时间的作用是为重构高维相空间提供新的独立坐标;

步骤三:按间隔τ从时间序列构成奇异吸引子轨迹向量 yj=(xj，xj+τ，…xj+(m－1)τ)。

3 GRNN神经网络目标检测

通过重构相空间我们得到了海杂波混沌动力系统在重构相空间中的一条轨迹，该轨迹正是产生海杂波的内在非线性系统状态转移方程H的一个样本:

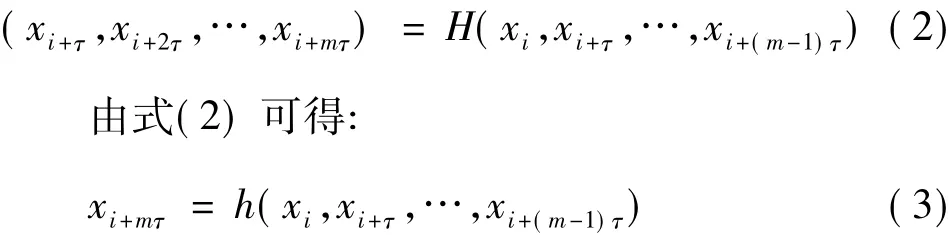
此即为海杂波预测方程［9，10］。

但是考虑到增加的变量能够提供系统更多的信息，使之具有更大的灵活性和函数概括的能力，我们采用 S.Haykin 提出的 xi+mτ=h(xi，xi+1，xi+2，…，xi+mτ－1)作为实际预测函数。

广义回归神经网络(GRNN)是美国学者Donald F.Specht在1991年提出的，他是径向基神经网络的一种。GRNN在预测能力和学习速率上有较强的优势。

GRNN 神经网络［11，12］由径向基神经元和线性神经元构成，其中径向基网络传递函数采用radbas，表达式为:radbas(n)=e－n2。它由输入层、模式层、求和层和输出层四层组成，如图2所示。

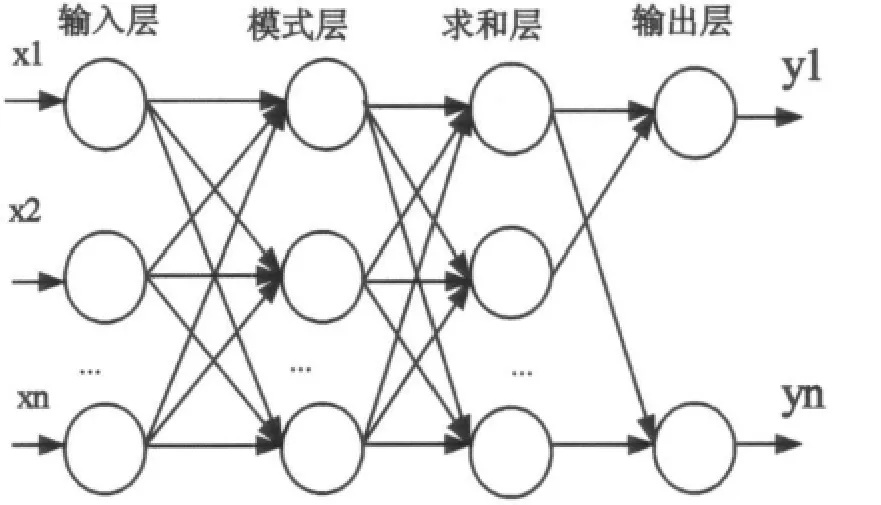
图2 广义回归神经网络原理图

输入层神经元个数有学习样本中输入向量的维数决定，各神经元是简单的分布单元，直接将输入变量传递给模式层。模式层的神经元个数等于学习样本的数目。求和层是使用两种类型神经元求和。输出层中的神经元个数等于学习样本中输出向量维数。

对没有目标的海杂波相空间重构时间序列建模，将GRNN神经网络训练成一个预测器，根据GRNN神经网络结构可以得出，当训练样本确定后，其网络结构和各神经元之间的连接权值是确定的。在训练网络过程中，只是调整平滑因子一个参数，来获得最佳网络，所以采用GRNN这种网络来进行目标检测具有高速性［13］。网络训练好后，对接收到得信号进行单步预测，得到预测值，计算对消误差和总误差均方根值。

对消误差:

总误差均方根值:

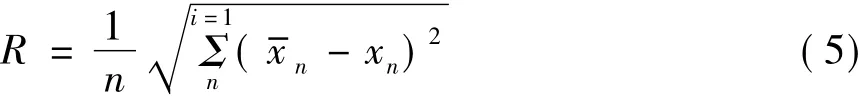
4 实验及结果分析

本文实验数据采用加拿大McMaster大学用IPIX雷达在Dartmouth地区海域实测带有小目标的海杂波数据，在此采用第#26组数据，即文件19931108－220902－starea.cdf.实测数据含有 14 个距离单元数据，每个距离单元相距 15m，含有131072个采样点，在第7距离单元含有一个直径为1m的球形弱小目标，该小球外表面为一层铝箔来增强目标信号。

采用互相关法确定τ为5，G－P法确定嵌入维数m为7［14］;因而设计的GRNN检测器的网络输入层为7，输出层为1。预测样本为28000，测试样本为5000。

为了得到最好的结果，实验采取了循环训练方法，当平滑因子为0.004时，MSE(Mean Square Error均方误差)最小，此时GRNN网络检测器最佳，见表1。

表1 循环训练获得的平滑因子和MSE(Mean Square Error均方误差)表

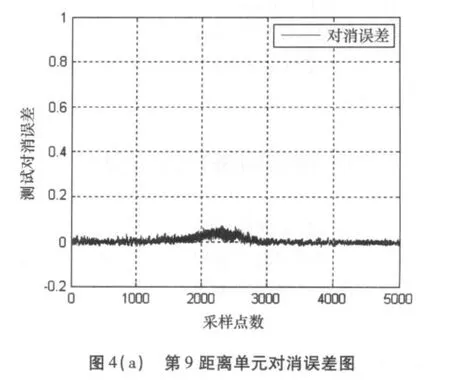
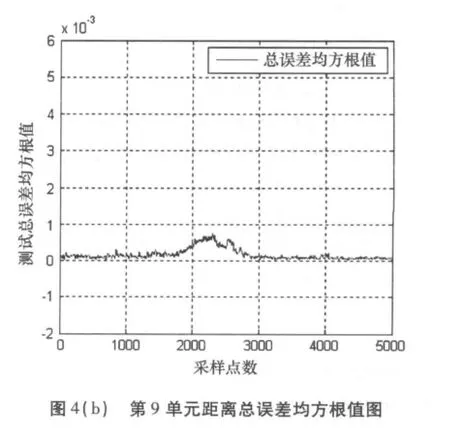
图3、图4分别为#26数据第4和第9距离单元(纯海杂波)的对消误差图和总误差均方根值图，误差几乎为零。

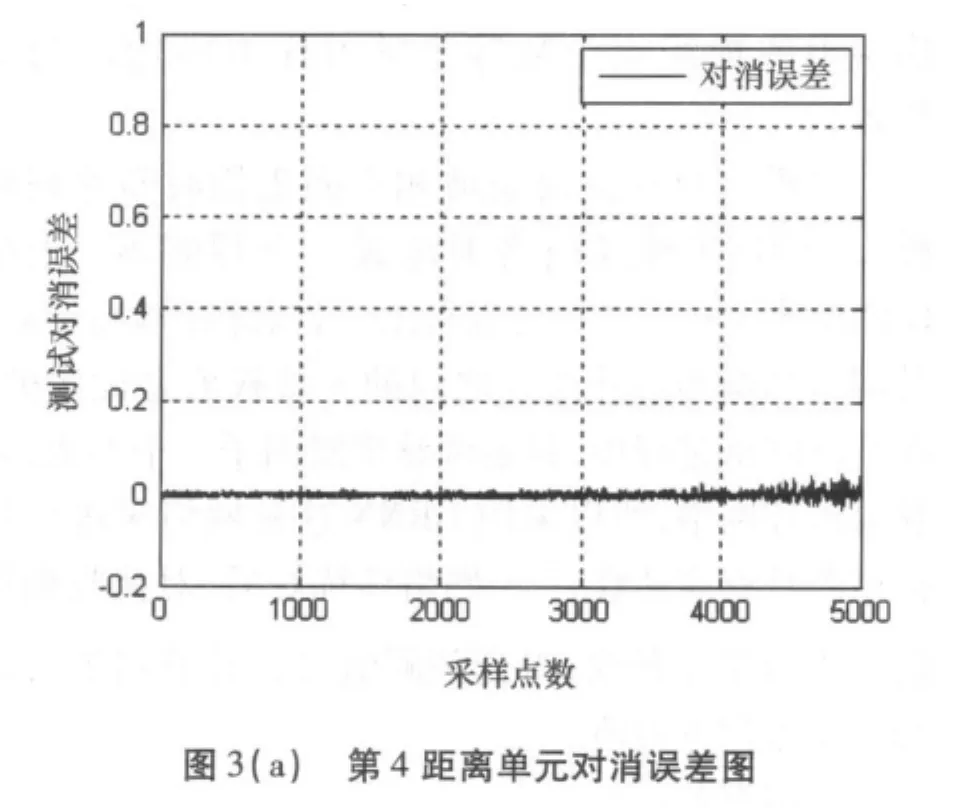
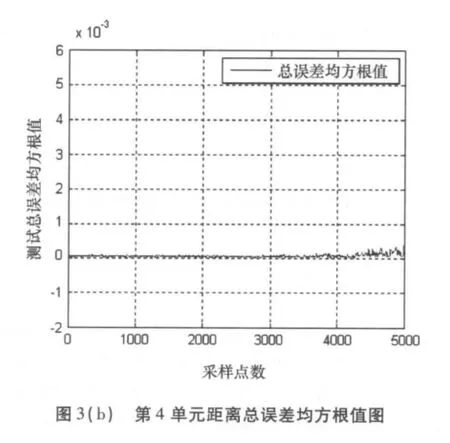
图5为#26数据第7距离单元(含有小目标)的对消误差和总误差均方根值图，误差明显。由此，可以根据对消误差和总误差均方根值来判定此距离单元是否含有目标。

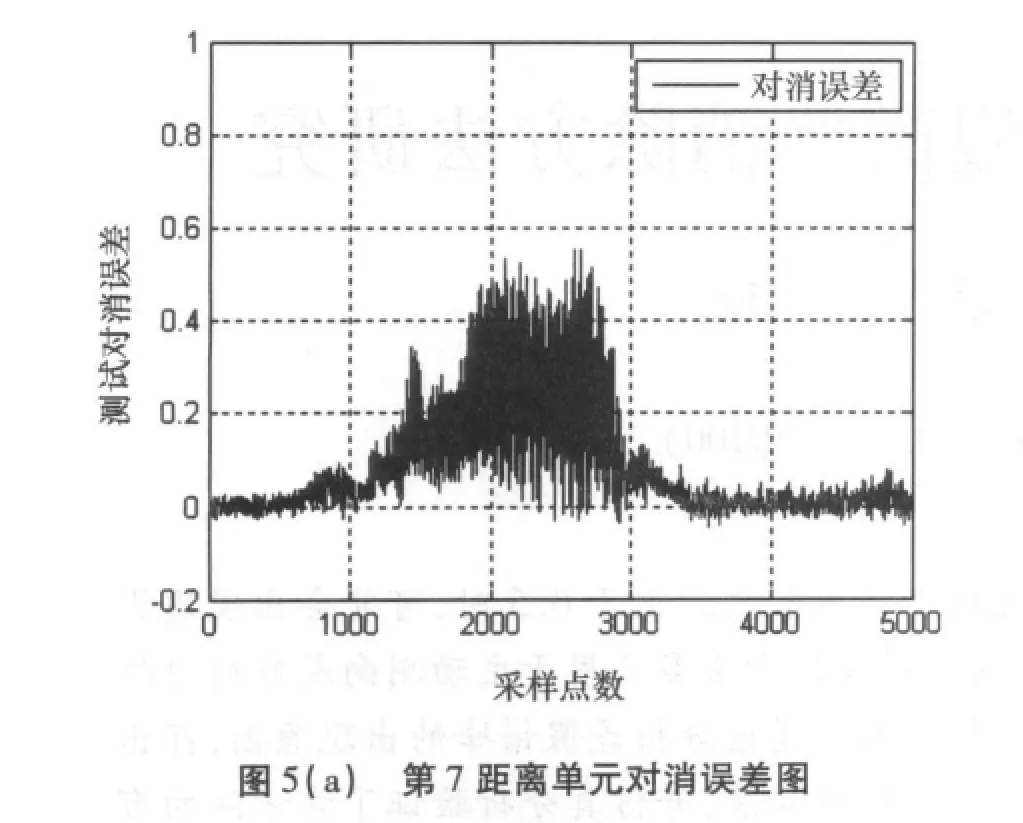
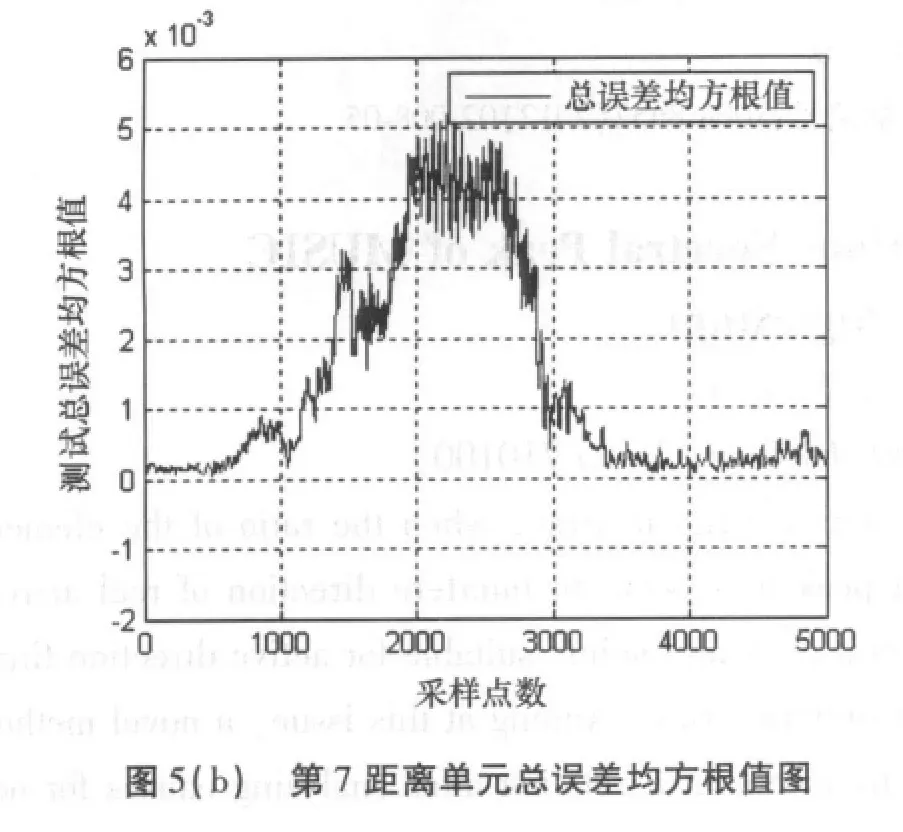
5 结束语

本文利用海杂波的混沌特性，首次提出用GRNN神经网络检测海杂波数据中目标并验证了此方法具有良好效果。含有目标的距离单元数据的对消误差和总误差均方根值很大，纯海杂波情况下对消误差和总误差均方根值趋近零。因为GRNN网络只需要调节平滑因子这一个参数即可获得最佳网络，所以此种网络具有高时速性。事实上，由于海杂波混沌特性方面的主要问题是在噪声背景下如何判别海杂波的混沌特性，即如何在去除噪声才不影响海杂波的内在特性的前提下，再对海上目标进行检测。尽管如此，这种方法还是可以应用到很多领域，比如短时路口交通量预测、港口船只流量预测等。以后的工作重点将是提取更多的目标因素作为网络输入，减少噪声对海杂波内在特性的影响，以提高目标预测的准确性。

［1］钱玉莹，王哲.基于混沌理论的海杂波处理方案设计［J］.科学技术与工程，2010，1671－1815(2010)6－1398－04.

［2］Leung H，Haykin S.Is there a radar clutter attractor［J］.Apply Physics Letters，1990，6(5):593－595.

［3］姜斌，王宏强，黎相等.S波段雷达实测海杂波混沌分形特性分析［J］.电子与信息学报，2007，8(4):1809－1812.

［4］姜斌，王宏强，付耀文等.基于LS－SVM 的海杂波混沌预测［J］.自然科学进展，2007，17(3).

［5］Haykin S，Xiaobo Li.Detection of signals in chaos［J］.Proceedings of the IEEE，1995，83(1):95－122.

［6］Takens F.Detecitng Strange Attraciton in Turbulence［M］.Beriln:Sprniger-Veralg，1981.

［7］K ennel M B，Brown R，Abarbanel H D J.Determinning embeding dimension for phasespace reconstructoin using a geometrical constructoin［J］.Phys.Rev.A，1992，45(6):3403－3411.

［8］Fraser Andrew M，Swinney Harry L.Independent coordinates for strange attractors［J］.Physical Review A，1986，33(2):1134－1140.

［9］林三虎，朱红，赵亦工.基于神经网络的海杂波模型［J］.红外与毫米波学报，2004，23(1):55－58.

［10］陈瑛，罗鹏飞，曾勇虎.基于RBF神经网络的海杂波建模［J］.系统仿真学报，2007，19(3):524－526.

［11］冯志鹏，宋希庚，薛冬新.基于广义回归神经网络的时间序列预测研究［J］.振动、测试与诊断，2003，23(2):105－109.

［12］林强，陈一梅.神经网络模型在港口吞吐量预测中的应用与误差分析［J］.水道港口，2008，29(1):72－76.

［13］魏晋雁.采用GRNN模型进行交通量预测及实现研究［J］.长沙交通学院学报，2006，22(2):46－50:425－420.

［14］王福友.海杂波混沌分形特性分析、建模及小目标检测［D］.哈尔滨工程大学，2008.