氧枪布置方式对底吹熔池熔炼过程的影响

闫红杰，刘方侃，张振扬，高 强，刘 柳，崔志祥，申殿邦

(1. 中南大学 能源科学与工程学院，长沙 410083；2. 中南大学 流程工业节能湖南省重点实验室，长沙 410083 3. 东营方圆有色金属有限公司，东营 257091)

氧枪布置方式对底吹熔池熔炼过程的影响

闫红杰1,2，刘方侃1,2，张振扬1,2，高 强1,2，刘 柳1,2，崔志祥3，申殿邦3

(1. 中南大学 能源科学与工程学院，长沙 410083；2. 中南大学 流程工业节能湖南省重点实验室，长沙 410083 3. 东营方圆有色金属有限公司，东营 257091)

采用FLUENT软件，分别选择k−ε系列湍流模型和雷诺应力模型(RSM)对底吹熔池熔炼炉内的高温熔体气液两相流进行数值模拟，并且依据相似原理，通过水模型实验对数值模拟结果进行验证，综合评价发现Realizablek−ε模型的计算精度最高。选用Realizablek−ε模型，对氧枪布置方式及直径对底吹熔池熔炼过程的影响进行数值模拟研究，结果表明：在一定范围内，适当增大氧枪倾角有利于底吹熔池熔炼过程的进行，当单排氧枪倾角在17°～22°之间时，熔池各指标均处于较好的水平；相对于现场工况，双排氧枪倾角分别为12°和22°时，熔池的搅拌效果显著增强；当氧枪倾角为20°时，其有效搅拌区直径为1.475 m，对应的合理氧枪间距为0.98～1.23 m；适当减小氧枪直径可以有效提高熔池气含率。

底吹熔池熔炼；湍流模型；氧枪；数值模拟

Abstract:FLUENT was used to simulate the high temperature melt multiphase flow in oxygen-enriched bottom-blowing bath smelting furnace with a series ofk−εmodels and Reynolds stress model. Based on similar principles to verify and compare the numerical simulation results with water model experiment. It is indicated that the realizablek−εmodel has the best result. Realizablek−εmodel is chosen to simulate the influence of lance arrangement and diameter on the oxygen-enriched bottom-blowing bath smelting process. Based on the result, appropriate increase of the lance inclination is helpful for oxygen-enriched bottom-blowing bath smelting process, and when a single row of lance inclination between is 17°−22°, the bath indicators are all in a good level. Relative to site conditions, when the double lance inclinations are 12° and 22°, the bath mixing effects are significantly enhanced. When the lance inclination is 20°, the effective mixing zone diameter is 1.475 m, corresponding to the best lance spacing of 0.98−1.23 m. Appropriately reducing lance diameter can effectively increase the bath gas rate.

Key words:oxygen-enriched bottom-blowing bath smelting; turbulence model; lance; numerical simulation

在冶金工业中，冶金炉窑中的高温流体(如金属熔体、高温烟气等)多相流动参数是影响冶金工艺的一个重要因素，它不仅关系到冶金反应的效率，还决定着冶金炉窑的安全使用寿命。相比于传统研究方法，由于数值模拟方法具有计算结果信息全、周期短、费用低、安全可靠等优点，已经成为研究高温流体多相流动的重要方法。目前，对于高温流体多相流动的数值模拟，通常使用基于涡粘性假设下的湍流模型，如混合长度模型[1]、标准k−ε模型[2]及其相关改进模型和雷诺应力模型[3]等。因此研究各湍流模型对高温流体多相流动的模拟能力很有必要。

LI等[4−5]利用VOF多相流模型和标准k−ε湍流模型模拟了底吹钢包内气/钢液/渣的三相流动，模拟结果再现了底吹钢包内气/钢液/渣三相流动现象，分析了 Ar喷吹流量变化对渣眼无量纲面积和渣眼周围的钢液向下流动速度的影响。SHAMSI等[6]使用Realizablek−ε湍流模型模拟了连铸板坯连铸机铸坯的流体流动、传热和凝固过程，预测分析了铸坯中流体的速度和温度分布及模具的换热系数。雷鸣等[7]选用标准k−ε湍流模型对还原熔融炉进行了顶侧复吹计算，研究了顶枪枪位和气体流速对铁浴的搅拌影响。ZHOU等[8]模拟了回转窑废铝熔化过程，预报了炉子上部烟气湍流燃烧状况和废铝熔化所需时间及天然气消耗量。很多学者在这方面做了大量的研究工作，但是都没有系统地对各湍流模型的模拟能力进行比较，并且基于RNGk−ε模型和雷诺应力模型(RSM)方法的数值模拟研究较少。本文作者首先以底吹熔池熔炼炼铜炉为研究对象，结合水模型实验验证，对标准k−ε模型(ske)、Realizablek−ε模型(rke)、RNGk−ε模型和雷诺应力模型(RSM)就高温流体多相流动的模拟能力进行了比较分析，通过比较分析选择了合适的湍流模型。

氧枪是底吹熔池熔炼工艺的核心技术[9]，因此研究底吹熔池熔炼炉的氧枪布置方式及直径对其熔炼过程的影响，对优化底吹熔池熔炼工艺具有重要意义。DAVIS等[10−11]对HIsmelt工艺中的熔融还原炉进行了数值模拟，研究了顶吹氧枪和侧吹氧煤喷枪作用下流动和传热的影响。詹树华等[12]对深浸入式侧吹方式下试验炉内熔池拌现象进行了研究，采用气液两相多流体模型描述了侧吹熔池内两相流运动和熔池搅动的基本特征。本文作者通过对各湍流模型的比较研究，选择了可靠的数学模型，并且使用选择的数学模型，以熔池气含率、熔池流体平均运动速度及湍动能等参数为指标对底吹熔池熔炼炉的氧枪的单、双排倾角、间距和直径对熔池熔炼过程的影响进行了数值模拟研究，得到了其影响规律。

1 模型建立

1.1 物理建模

以山东某公司的自主知识产权底吹熔池熔炼炉[13]为研究对象，其结构示意图如图1所示。

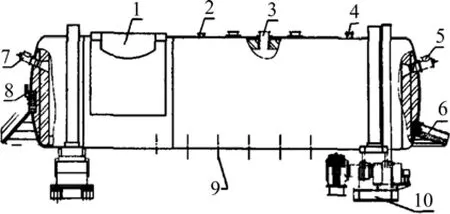
图1 底吹熔池熔炼炉示意图Fig.1 Sketch map of bottom-blowing bath smelting furnace:1—Gas vent; 2—Temperature measuring hole; 3—Feed opening; 4—Probe hole; 5—Main burner; 6—Copper export;7—Aided burner; 8—Slap tap; 9—Lance; 10—Transmission

底吹熔池熔炼炉内形成一定高度的熔池，精矿由加料口加入到底吹熔池熔炼炉中，富氧空气由底部的双排氧枪喷吹进入熔池熔炼炉，精矿被高温熔体卷吸到熔池中与氧气发生剧烈的熔炼与造渣反应，最后铜锍和渣分别由铜锍放出口和放渣口放出，完成底吹熔池熔炼过程。

本文作者主要研究底吹熔池熔炼炉内熔池中高温熔体的气液两相流动，假设初始状态时熔池为静止的，暂时不考虑其中的化学反应，也不考虑加料和放铜锍、渣对熔池的扰动，不考虑壁面的散热。如图1所示，熔池熔炼炉长度为14.8 m；氧枪直径为0.06 m，一共9支，分两排交叉布置，分别与竖直方向夹角为7°和22°，其中夹角为7°的有5支，22°的有4支，单排氧枪间距为1.3 m；熔池熔炼炉内径为3.5 m；熔池高度为1.35 m。

1.2 数学建模

1.2.1 基本控制方程

采用 VOF两相流模型模拟熔池熔炼炉内的气液两相流动，采用几何重构方案描述气液自由表面。VOF两相流控制方程和自由表面几何重构方案详见文献[14]。对于气液两相流，计算中定义体积函数α(单元中流体所占体积与单元体积之比)，通过建立和求解α的输运方程来确定自由表面的位置。当体积函数α=1，则单元体积内充满液体；α=0，则单元体积内无液体；α=0～1之间，则单元体积内既充有液体又充有气体，此单元为自由表面单元。

1.2.2 湍流模型

1)k−ε系列湍流模型

k−ε系列湍流模型[15−17]具有相同形式的k和ε输运方程，只是其各自对其模型常数的计算方法不同。通用的k和ε的输运方程可分别表示为

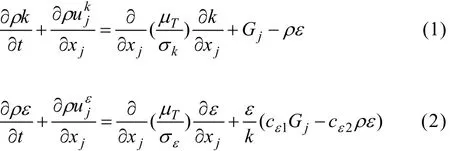
式中：Tμ是一个假设存在的“湍流黏度”，

k−ε系列湍流模型的模型常数如表1所列。

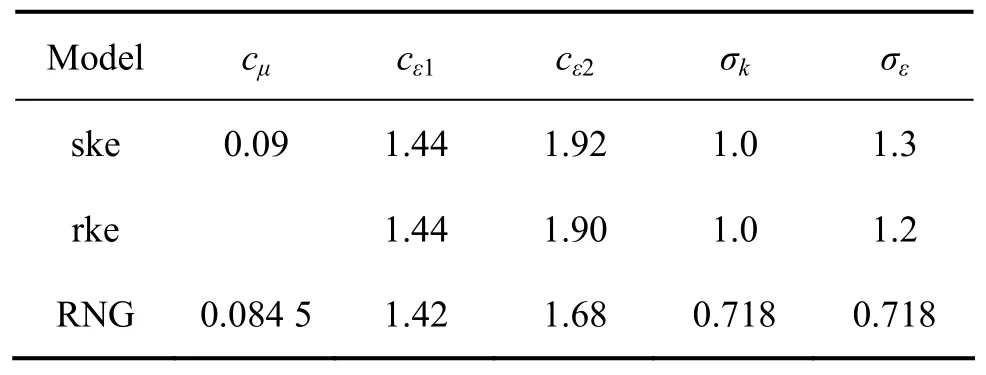
表1k−ε系列湍流模型常数Table 1 Model constants ofk−εmodels

其中在Realizablek−ε模型(rke)中，cμ不再是一个常数，而与应变率联系起来，是一个变量。

2) 雷诺应力模型(RSM)

雷诺应力模型(RSM)[18]通过求解雷诺应力输运方程来封闭基本方程组，雷诺应力输运方程可表示为

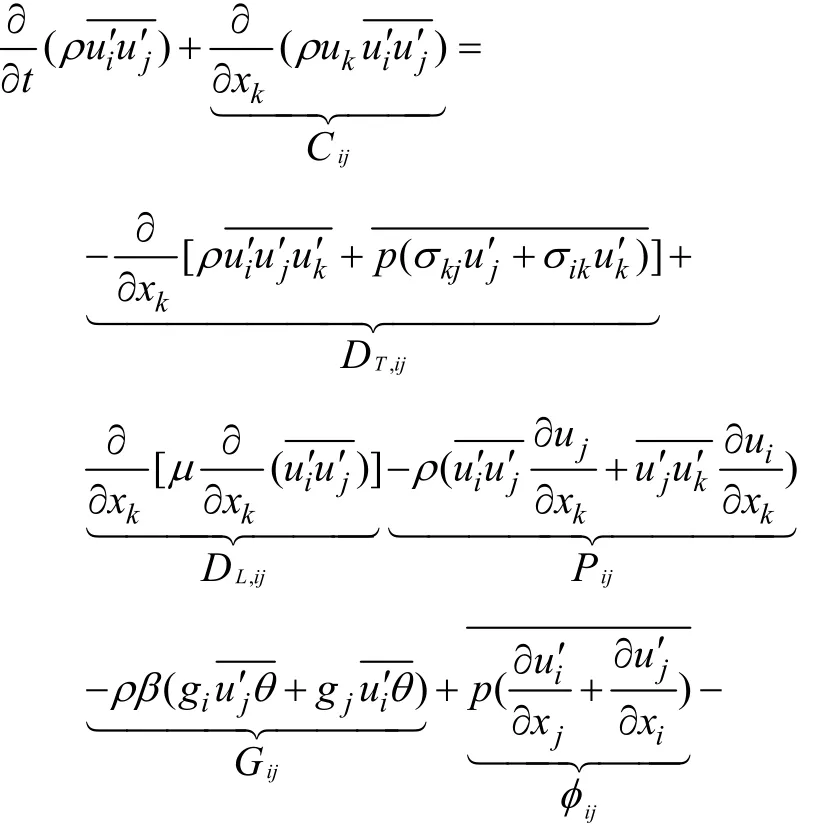
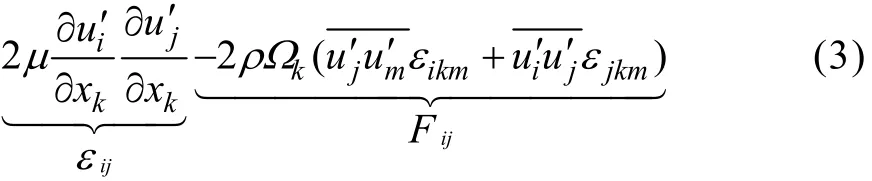
其中：cij为对流项；DT,ij为湍流扩散项；DL,ij为分子扩散项；Pij为应力产生项；Gij为浮力产生项；ijφ为压力应变项；εij为耗散项；Fij为系统旋转产生项。

RSM模型的k和ε的输运方程可分别为

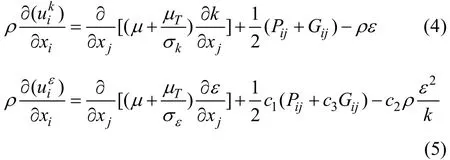
对于不可压缩流体，Gij浮力产生项为0，其他模型常数分别如下：c1=1.44，c2=1.72，σk=0.82，σε=1.0，

c3=

2 边界条件及求解策略

2.1 边界条件及物性参数

2.1.1 入口条件

氧枪入口为质量入口边界条件，入口工质为可压缩富氧空气，入口质量流量为0.48 kg/s，入口温度为300 K，湍流强度和湍动能耗散率均为5%，水力学直径为0.06 m。

2.1.2 出口条件

烟气出口设置为压力出口边界条件，出口压力设置为−10Pa。

2.1.3 壁面边界条件

不考虑壁面的散热，作绝热壁面处理；认为在壁面处的流体速度为 0，采用无滑移壁面边界条件；近壁区域采用标准壁面函数处理。

2.1.4 物性参数

不考虑化学反应，底吹熔池熔炼炉内包含铜锍熔体和富氧空气(烟气)两种流体，由于气体入口马赫数大于0.3，故富氧空气作理想可压缩气体处理，具体物性参数如表2所列。

2.2 求解策略

通过网格独立性检查，在GAMBIT中进行网格画分。对模型进行定时间步长的非稳态计算，时间步长为0.001 s，多相流模型选用VOF模型，压力速度耦合选择PISO算法，压力的离散化用PRESTO格式，为了提高计算精度，方程的离散化采用二阶迎风格式。

表2 底吹熔池熔炼炉内流体的物性参数Table 2 Property parameters of fluids in bottom-blowing bath smelting furnace

3 模型验证

实验验证依据相似原理，在实验室搭建与熔池熔炼炉原始尺寸10:1比例的有机玻璃实验平台，如图2所示。实验材料使用压缩氮气和水，实验平台的数据提取主要借助于高速摄影仪。为了减少计算量，实验验证选择二维底吹熔池熔炼炉纵截面进行。依据实验平台与数值模拟模型的修正弗拉德数相等对各湍流模型的数值模拟结果进行实验验证，从而得到对于高温熔体多相流计算精度最高的湍流模型。

图2 水模型实验平台Fig.2 Water model experiment platform

3.1 氧枪根部气泡形态

富氧空气由氧枪进入熔池形成气泡是一个非常复杂的过程，铜锍熔液和气体的各项参数(如压力、速度、温度等)都发生有明显的变化；此外，氧枪根部的气泡形成于近壁区域，近壁区域属于湍流模型计算的薄弱环节，因此，氧枪根部气泡形态是衡量各湍流模型模拟能力一个重要参数。各湍流模型计算的氧枪根部气泡形态如图3所示。

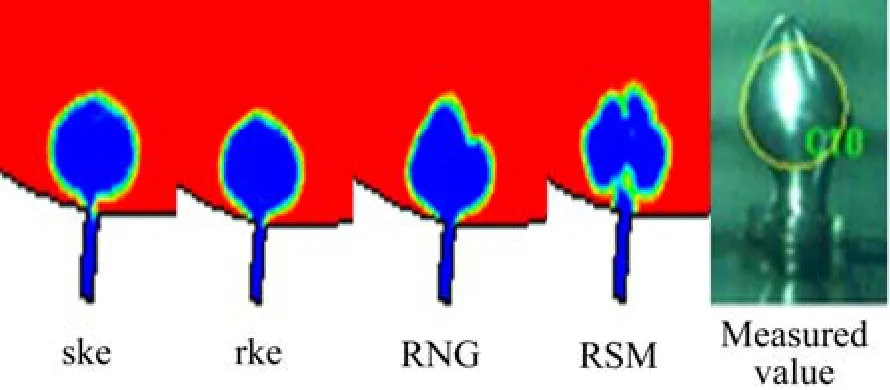
图3 氧枪根部气泡形态比较Fig.3 Comparison of bubbles form at bottom of lance

由图3氧枪根部气泡形态的比较可以很直观地发现，rke模型和ske模型模拟的气泡形态与实测气泡形态很接近，富氧空气由氧枪进入熔池后会在氧枪根部处形成一定尺寸的椭球形气泡。RNGk−ε模型和RSM模拟的氧枪根部气泡存在明显的变形，与实际不符合，模拟效果差。

3.2 氧枪根部气泡尺寸

各湍流模型计算的气泡尺寸与氧枪直径之比如表3所列。

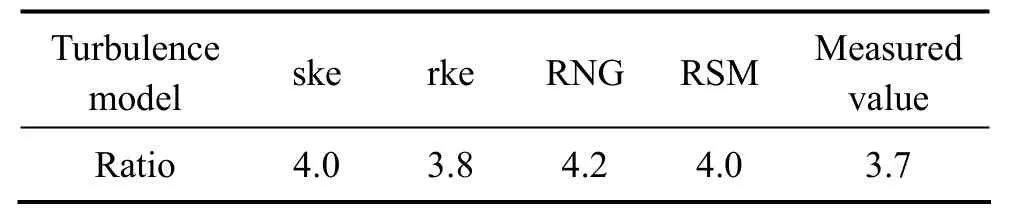
表3 气泡尺寸与氧枪直径之比Table 3 Ratio of size of bubble and lance diameter

由表3可知，各湍流模型计算的氧枪根部气泡尺寸均比实际值偏大，其中rke模型的模拟效果最好，相对误差仅为2.7%；ske模型和RSM的模拟效果相当，误差为8.1%；RNGk−ε模型的模拟效果最差。氧枪出口区域属于近壁区域，在固体壁面附近由于分子粘性的作用，湍流的脉动受到阻尼，Re数会很小，k−ε系列模型和 RSM模型都属于高Re数的湍流计算模型，因此，在近壁区域直接使用就不合适了，本文作者采用标准壁面函数对近壁区域进行处理，由计算结果可知，rke模型和标准壁面函数的联合处理效果最优；此外，RSM模型为五方程模型，计算速度也相对慢很多。

3.3 气泡平均上浮速度

气泡平均上浮速度定义为气泡产生到完全达到液面这段行程的平均速度。气泡从产生到脱离，再通过上浮运动到液面是一个极为复杂的湍流流动过程，因此气泡平均上浮速度计算的准确性也是衡量湍流模型模拟能力的重要依据。表4所列数值模拟数据和实测数据来自于氧枪产生的第一个气泡的平均上浮速度。

由表4可知，ske模型和rke模型的计算结果很接近实测数据，而RNGk−ε模型和RSM的计算结果均偏大。气泡在上浮过程中主要受到重力、浮力、表面张力以及粘性切应力的影响。相对于ske模型，rke模型的cμ不再是一个常数，专门考虑了旋转对湍流的影响，对于相间作用力的处理能力更强，相对误差远小于5%。

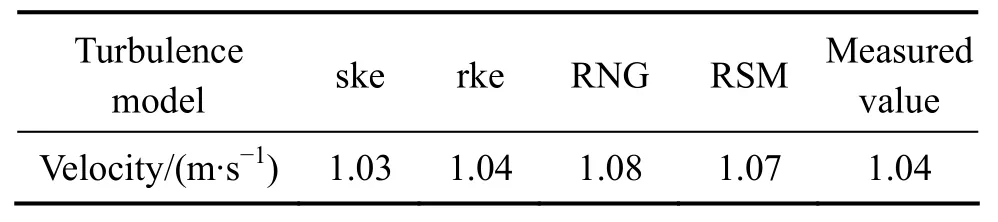
表4 气泡平均上浮速度Table 4 Average speed of floating bubbles

因此，由以上对各湍流模型的实验验证结果可知：各湍流模型对于高温熔体气液两相流流场均有一定的模拟能力，均能在一定程度上反映相应的速度场、压力场、浓度场和温度场等信息，但是各湍流模型针对高温熔体多相流的模拟能力差异很大，综合比较发现Realizablek−ε模型的效果最佳，误差在5%以内，模拟结果可靠。

4 氧枪布置方式及直径对底吹熔池熔炼过程的影响

由实验验证可知，Realizablek−ε模型对于高温熔体多相流的模拟效果最佳，因此选择 Realizablek−ε模型对底吹熔池熔炼炉的核心部件氧枪的布置方式及直径对其熔炼过程的影响进行了数值模拟研究。

4.1 氧枪倾角影响

4.1.1 单排氧枪倾角

单排氧枪倾角研究在控制氧枪入口流量不变的前提下进行，建立二维底吹熔池熔炼炉纵截面的不同角度的氧枪喷吹模型，对每个模型进行计算并提取数据，可以得到熔池稳定后相应氧枪角度条件下的熔池气含率、流体平均速度及湍动能与氧枪倾角的关系。

实验对设计的7组氧枪角度进行分析，分别为0°、7°、12°、17°、22°、27°和32°，每组模型计算时间为10 s。

熔池稳定后不同角度氧枪条件下的熔池气含率、湍动能及流体平均速度分布分别如图4～6所示。

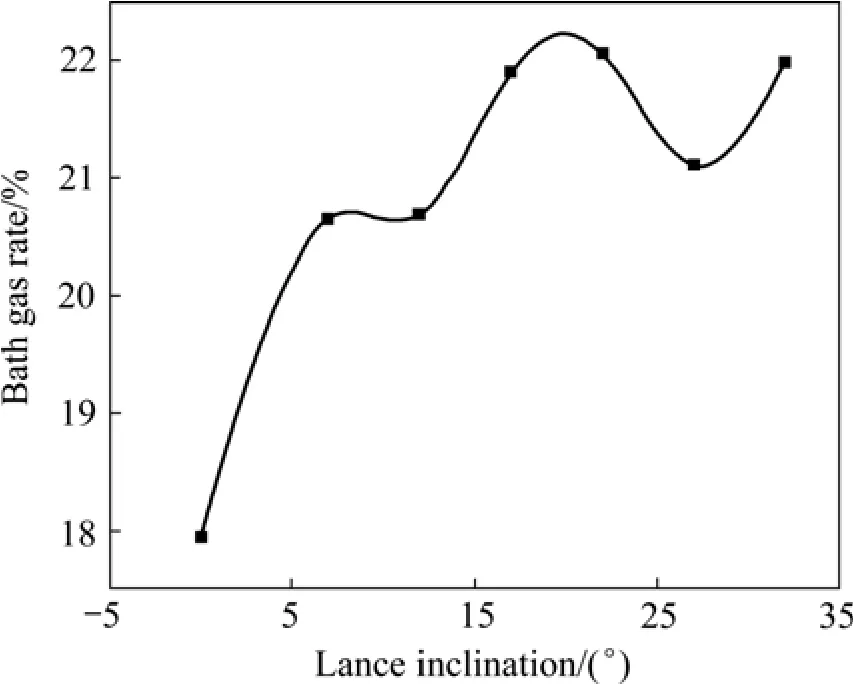
图4 熔池气含率与氧枪倾角的关系Fig.4 Relationship between bath gas rate and lance inclination

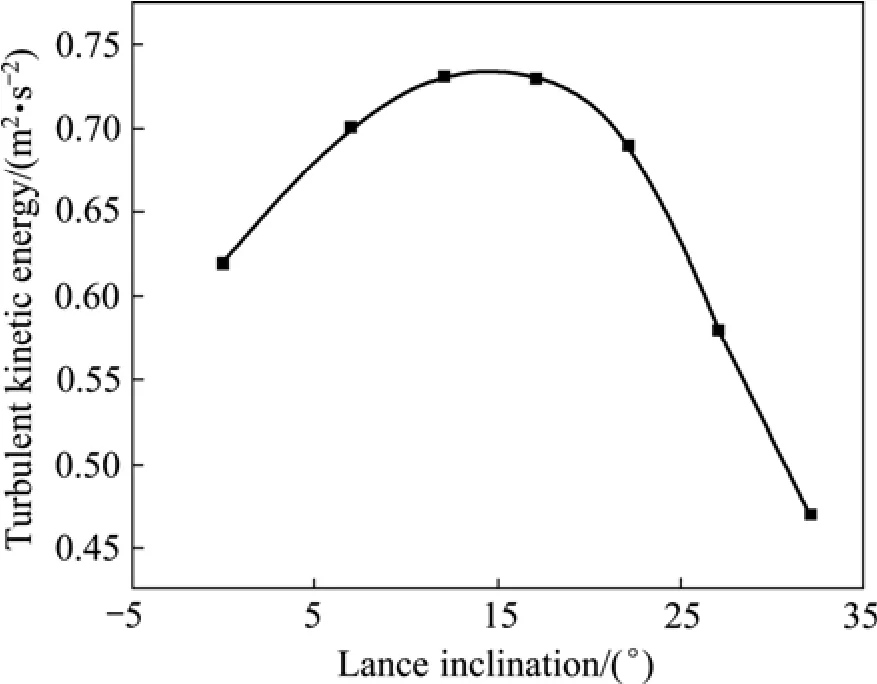
图5 湍动能与氧枪倾角的关系Fig.5 Relationship between turbulent kinetic energy and lance inclination

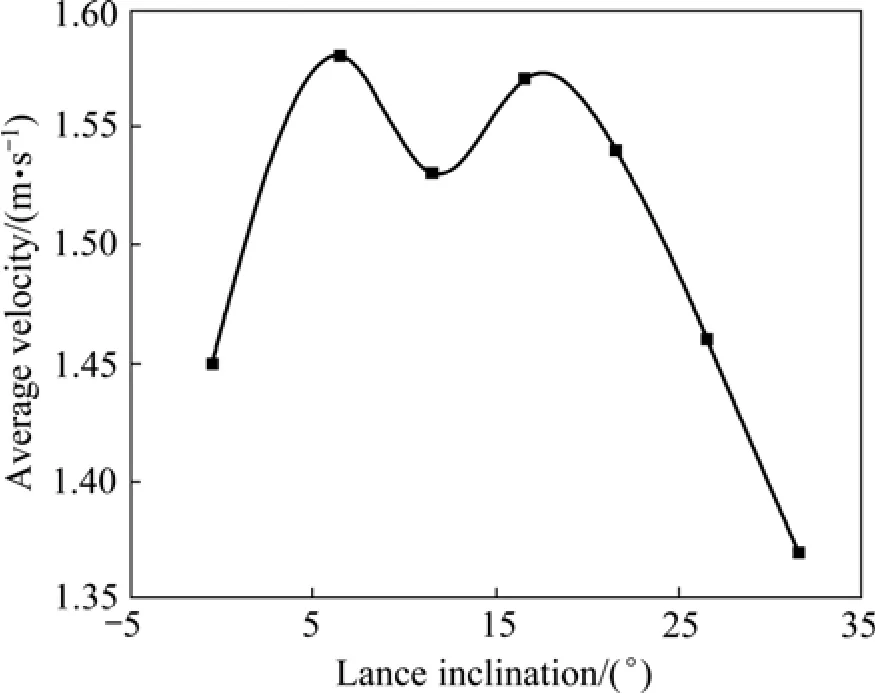
图6 熔体平均速度与氧枪倾角的关系Fig.6 Relationship between melt average velocity and lance inclination

综合分析图4、5和6可知：熔池稳定后，在氧枪倾角为0°～22°之间时，熔池气含率随着氧枪倾角的增大而不断增加，在 17°～22°之间达到最大值；随后随着氧枪倾角的增大，熔池气含率不断降低，当氧枪倾角大于 27°时，熔池气含率又随着氧枪倾角的增大而增加；流体平均速度随氧枪倾角的增大呈现“M”型曲线分布，两个峰值分别出现在7°和17°处，氧枪倾角大于 22°时，流体平均速度很小；流体平均湍动能随着氧枪倾角的增大呈现抛物线状的分布，在氧枪倾角为17°时到达最大值。对这3个参数综合评价分析可得：当氧枪倾角为 17°～22°之间时，熔池各项指标均处于较高的水平。

4.1.2 双排氧枪倾角

通过单排氧枪倾角的研究得到的氧枪倾角为17°～22°之间时，熔池各项指标均处于较好的水平。由于底吹熔池熔炼炉本身为双排氧枪布置，分别是5支7°氧枪和4支22°氧枪，因此，在进行双排氧枪倾角研究时，建立熔炼炉的三维模型。为了简化计算、节约计算资源，将底吹炉考虑成仅有两支氧枪的双排结构，即将7°氧枪优化为12°，22°氧枪倾角不变，底吹炉轴向长度为2.6 m，氧枪间距为1.3 m，仿真结果如表5所示。

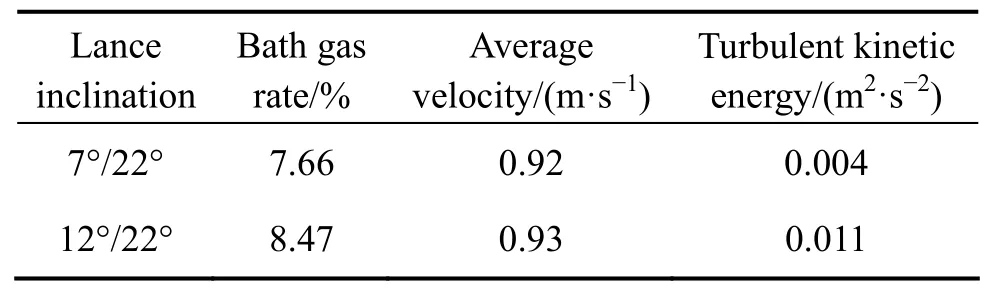
表5 双排氧枪仿真结果Table 5 Results of double lance simulation

由上表的数据分析可知，无论从哪个参数进行对比分析，12°/22°工况相对于7°/22°工况均有不同程度的优化。熔池气含率增大明显，平均速度略有优化，湍动能提高了一个数量级，因此，12°/22°工况明显优于7°/22°工况，熔池气含率水平和搅拌能力显著增强，有利于熔池熔炼过程的进行。

4.2 氧枪间距影响

在进行氧枪间距的研究时，先研究氧枪在最佳倾角下的有效搅拌区直径。假设有效搅拌区直径为S，氧枪间距为W，已有研究表明，当S/W=1.2～1.5之间时，氧枪间距最佳，既能保证氧气的高效吸收利用，又能防止搅拌死区的出现。

在氧枪倾角为 20°时，建立熔池熔炼炉的三维数学模型，得到熔池稳定后的有效搅拌区直径分布如图7所示。

分析图7可知，熔池达到稳定后，有效搅拌区直径随时间的变化不大，基本趋于稳定。提取数据可得，此种工况下有效搅拌区直径的平均值为1.475 m，又由当S/W=1.2～1.5时氧枪间距W为最佳可得，氧枪间距W=0.98～1.23 m，此时熔池熔炼炉的氧气利用和搅拌效果均处于较高的水平。

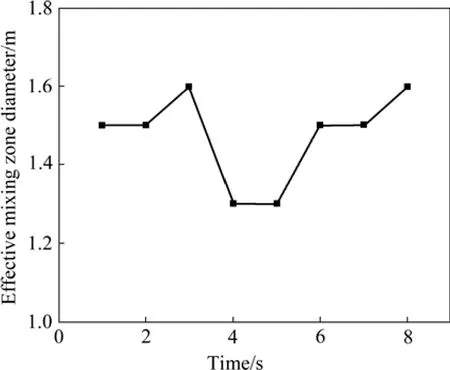
图7 有效搅拌区直径与时间分的关系Fig.7 Relationship between effective mixing zone diameter and time

4.3 氧枪直径影响

为了保证富氧空气有氧枪喷出进入熔池后流态不变，采取氧枪出口速度不变的策略进行氧枪直径的影响研究。建立二维底吹熔池熔炼炉纵截面数学模型，分别对氧枪直径由10 mm，每次增加10 mm，逐渐增大到60 mm的6组工况进行仿真研究，得到熔池稳定后的相关参数水平。由于氧枪出口速度不变，所以随着氧枪直径的增加，气体流量也不断增加。在氧枪流量不同时单纯考虑熔池气含率、流体湍动能和平均速度的水平作为评价指标就不合理了，因此在进行数据处理时，采用相关参数的相对变化值作为评价标准。以氧枪直径为10 mm时的数据为基准，比较其相关参数变化与直径变化之比，即θ′=(θ-θ10)/(D- 10) (其中θ、θ10、θ′分别是对应的参数值，直径为10 mm时的参数值和参数的相对变化值，D是对应的氧枪直径，单位为mm)，得到相关参数的相对变化值随氧枪直径的关系分别如图8～10所示。

综上分析可知：熔池气含率随氧枪倾角的增大而不断减小，说明减小氧枪直径有利于提高熔池气含率；平均湍动能和平均速度随氧枪直径的增大分别呈现正弦和余弦态曲线分布，其峰值均出现在氧枪直径为30 mm附近；当氧枪直径为40～50 mm之间时，熔池中各参数水平均较差。综合评价分析可得：当氧枪直径为30 mm时，熔池中各指标均处于较高的水平。

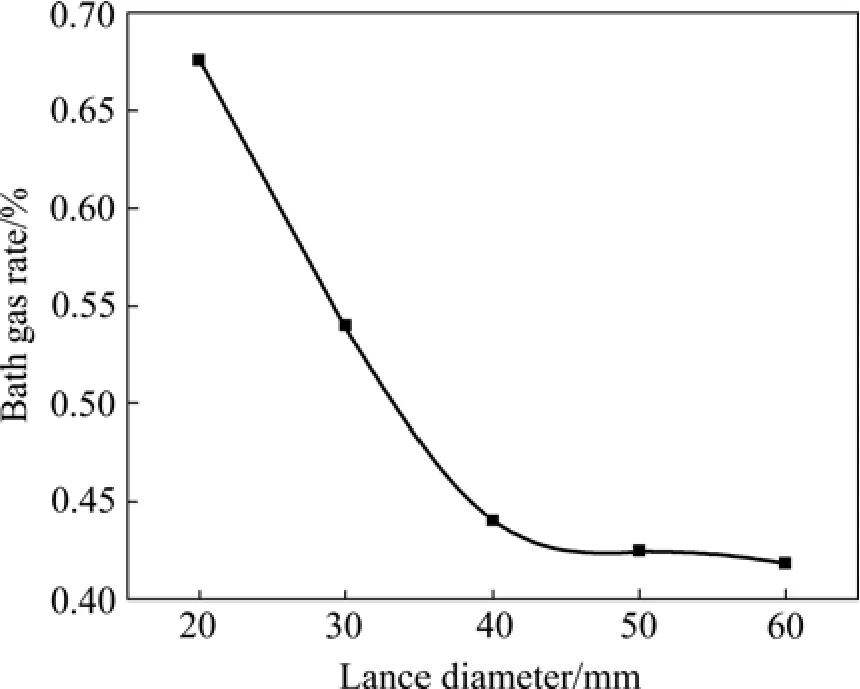
图8 熔池气含率相对变化值与氧枪直径的关系Fig.8 Relationship between relative bath gas rate and oxygen lance diameter

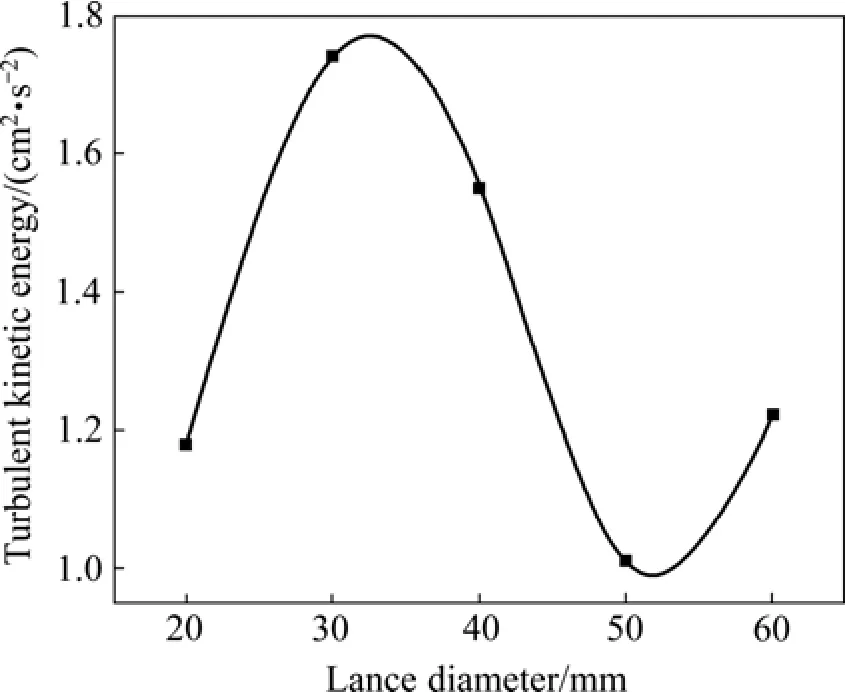
图9 湍动能相对变化值与氧枪直径的关系Fig.9 Relationship between relative turbulent kinetic energy and oxygen lance diameter

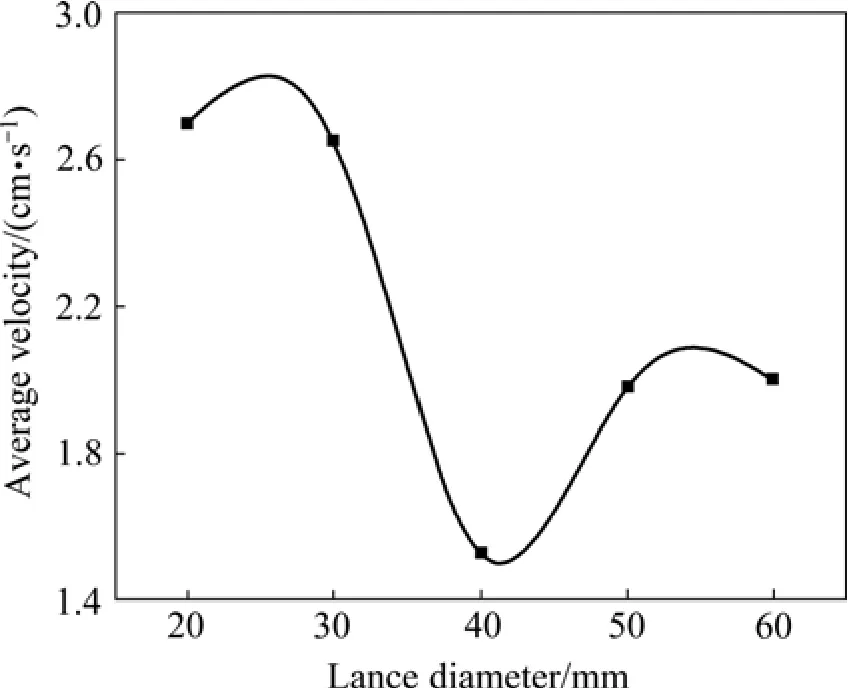
图10 熔体平均速度相对变化值与氧枪直径的关系Fig.10 Relationship between relative melt average velocity and oxygen lance diameter

5 结论

1) 建立了底吹熔池熔炼炉内高温熔体气液两相流的数学模型，并且依据修正的弗拉德数相等，对各湍流模型对于高温熔体气液两相流动的模拟能力进行了水模型实验验证，结果发现，Realizablek−ε模型对于高温熔体多相流的模拟效果最佳。

2) 在一定范围内，适当增大氧枪倾角有利于底吹熔池熔炼过程的进行，当单排氧枪倾角在 17°～22°之间时，熔池各项指标均处于较高的水平；相对于现场工况，双排氧枪倾角分别为12°和22°时，熔池的搅拌效果显著增强。

3) 当氧枪倾角为 20°时，其有效搅拌区直径为1.475 m，对应的合理氧枪间距为0.98～1.23 m。

4) 适当减小氧枪直径可以有效提高熔池气含率，当氧枪直径为30 mm时，熔池中各指标均处于较高的水平。

REFERENCES

[1] HSIEH K T, RAJAMANI R K. Mathematical model of the hydrocyclone based on physics of fluid[J]. AIChE Journal, 1991,37(5): 735−746.

[2] MALHOTRA A, BRANION R M R, HAUPTMANN E G.Modeling the flow in a hydrocyclone[J]. The Canadian Journal of Chemical Engineering, 1994, 72: 953−960.

[3] CHEN C J, JAW S Y. Fundamentals of turbulence modeling[M].Washington: Taylor&Francis, 1998.

[4] LI Bao-kuan, YIN Hong-bin, ZHOU C Q, TSUKIHASHI F.Modeling of three-phase flows and behavior of stag steel interface in an argon gas stirred ladle[J]. ISIJ International, 2008,48(12): 1704−1711.

[5] 李宝宽, 顾明言, 齐凤升, 王 芳, 周 谦. 底吹钢包内气/钢液/渣三相流模型及渣层行为的研究[J]. 金属学报, 2008,44(10): 1198−1204.LI Bao-kuan, GU Ming-yan, QI Feng-shen, WANG Fang,ZHOU Qian. Modeling of three-phase(gas/molten steel/slag)flows and slag layer behavior in an argon gas stirred ladle[J].Acta Metallurgica Sinica, 2008, 44(10): 1198−1204.

[6] SHAMSI M, AJMANI S K. Three dimensional turbulent fluid flow and heat transfer mathematical model for the analysis of a continuous slab caster[J]. ISIJ International, 2007, 47: 433−442.

[7] 雷 鸣, 王周勇, 张捷宇, 程伟玲, 郑少波, 王 波, 洪 新.多相流模型模拟熔融还原炉内流体流动[J]. 过程工程学报,2009, 9(z1): 420−428.LEI Ming, WANG Zhou-yong, ZHANG Jie-yu, CHENGWei-ling, ZHENG Shao-bo, WANG Bo, HONG Xin. Study on modeling of fluid flow in iron-bath smelting reduction furnace with multi-phase model[J]. The Chinese Journal of Process Engineering, 2009, 9(z1): 420−428.

[8] ZHOU B, YANG Y, REUTER M A, BOIN U M J. Modelling of aluminium scrap melting in a rotary furnace[J]. Minerals Engineering, 2006, 19: 299−308.

[9] 高长春, 袁培新, 陈汉荣. 氧气底吹熔炼氧枪浅析[J]. 中国有色冶金, 2006, 6: 13−17.GAO Chang-chun, YUAN Pei-xin, CHEN Han-rong. On lance for oxygen bottom-blown smelting[J]. China Nonferrous Metallurgy, 2006, 6: 13−17.

[10] DAVIS M P, DRY R J, SCHWARZ M P. Flow simulation in the HIsmelt process[C]//Proceedings of the Third International Conference on CFD in the Minerals and Process Industries.CSIRO, Melbourne, 2003, 12: 305−312.

[11] DAVIS M P, PERICLEOUS K, SCHWAZ M P. Mathematical modeling tools for the optimization of direct smelting process[J].Applied Mathematical Modeling, 1998, 22: 921−940.

[12] 詹树华, 赖朝斌, 萧泽强. 侧吹金属熔池内的搅动现象[J]. 中南工业大学学报: 自然科学版, 2003, 34(2): 148−151.ZHAN Shu-hua, LAI Chao-bin, XIAO Ze-qiang. CFD analysis of gas stirring behavior in side-blown metallic bath[J]. Journal of Central South University: Natural Science, 2003, 34(2):148−151.

[13] 崔志祥, 申殿帮, 王 智, 李维群, 边瑞民. 高底吹熔池熔炼炼铜新工艺[J]. 有色冶金: 冶炼部分, 2010, 3: 17−20.CUI Zhi-xiang, SHEN Dian-bang, WANG Zhi, LI Wei-qun,BIAN Rui-min. New process of copper smelting with oxygen enriched bottom blowing technology[J]. Nonferrous Metals:Extractive Metallurgy, 2010, 3: 17−20.

[14] RABHA S S, BUWA V V. Volume-of-fluid (VOF) simulations of rise of single/multiple bubbles in sheared liquids[J]. Chemical Engineering Science, 2010, 65: 527−537.

[15] 杨建伟, 杜艳平, 史 荣, 崔小朝, 刘 才. 异形坯连铸结晶器内三维流场的数值模拟[J]. 中国有色金属学报, 2001, 11(2):248−252.YANG Jian-wei, DU Yan-ping, SHI Rong, CUI Xiao-chao, LIU Cai. 3D numerical simulation on flowing distribution in mould for beam blank continuous casting[J]. The Chinese Journal of Nonferrous Metals, 2001, 11(2): 248−252.

[16] SHIH T, LIOU W W, SHABBIR A, YANG Zhi-gang, ZHU Jiang.A new k−e eddy viscosity model for high Reynolds number turbulent flows[J]. Computers Fluids, 1995, 24(3): 227−238.

[17] 伍成波, 殷恩生, 张 力, 刘永刚, 张丙怀, 唐 骞. 铝电解

槽高温烟气加热启动的三维温度场数值模拟[J]. 中国有色金属学报, 2003, 13(6): 1534−1538.

WU Cheng-bo, YIN En-sheng, ZHANG Li, LIU Yong-gang,ZHANG Bing-huai, TANG Qian. Numerical simulation of three-dimensional temperature field of gas start-up method for aluminum electrolysis cell[J]. The Chinese Journal of Nonferrous Metals, 2003, 13(6): 1534−1538.

[18] ZHANG Xiao-wei, JIN Xiao-li, WANG Yin, DENG Kang, REN Zhong-ming. Comparison of standard k−ε model and RSM on three dimensional turbulent flow in the SEN of slab continuous caster controlled by slide gate[J]. ISIJ International, 2011, 51(4):581−587.

(编辑 龙怀中)

Influence of lance arrangement on bottom-blowing bath smelting process

YAN Hong-jie1,2, LIU Fang-kan1,2, ZHANG Zhen-yang1,2, GAO Qiang1,2, LIU Liu1,2, CUI Zhi-xiang3, SHEN Dian-bang3
(1. School of Energy Science and Engineering, Central South University, Changsha 410083, China;2. Hunan Key Laboratory of Energy Conservation in Process Industry, Central South University, Changsha 410083, China;3. Dongying Fangyuan Non-ferrous Metal Co., Ltd., Dongying 257091, China)

TF811

A

1004-0609(2012)08-2393-08

国家高技术研究发展计划资助项目(2010AA065201)；中南大学自由探索计划资助项目(2011QNZT097)

2011-08-11；

2012-02-20

闫红杰，教授，博士；电话：13873102530；E-mail: s-rfy@csu.edu.cn