基于FDTD的非线性混合电路特性分析

梅诣偲， 吴先良， 黄志祥， 鲁思龙， 任信钢， 杜红梅

（1.安徽大学 电子信息工程学院，安徽 合肥 230601；2.合肥师范学院 物理电子系，安徽 合肥 230601）

随着电子技术的发展，电路的工作频率越来越高，集总元件的尺寸相对于波长越来越小，对于一些结构很复杂或者工作频率很高的系统，电路元件参数的提取已十分困难，路的概念也变得非常模糊。因此传统的电路理论就很难高效精准地进行电路特性分析，场分析方法才是有效的分析手段，其中FDTD方法以其通用性强、程序简单等优点得到了大量应用。FDTD思想自文献［1］提出以来在电磁领域得到推广应用［2－3］，文献［4］将其应用于无源集总元件，文献［5－6］将其推广到了三维情况，文献［7］首次运用FDTD算法进行有源天线的分析，并得到了正确结果。近年来FDTD在微波电路上的应用更加广泛，文献［8］运用FDTD方法对微带线直角拐角进行弧形切角研究，找到了最佳弧形切角，并验证最佳切角的存在，文献［9］提出了一种二极管计算的新方法，提高了计算效率。

本文在此基础上，运用FDTD方法，采用非分裂完全匹配层技术（UPML）［10］，推导了基于D－H关系的集总元件的FDTD三维迭代公式，对高频信号下非线性单管混频器进行了全波分析，得到的各个时刻电路间场分布图以及混频器二极管两端电压波形与软件仿真结果高度吻合，证明了此方法有效可行。

1 理论推导

集总元件处于真空中时麦克斯韦旋度方程：

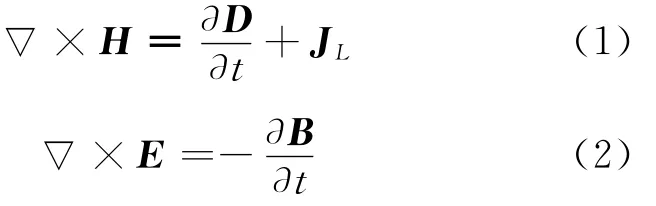
其中，H、D、E、B分别为磁场强度、电位移、电场强度、磁感应强度；JL为集总元件的电流密度。

假设JL沿z方向，如图1所示，则JL＝JzL＝IzL／（ΔxΔy），由此可导出集总元件处FDTD迭代公式。由于UPML的公式基于D－H 关系导出，故此处也给出D－H关系式，以Dz为例，即

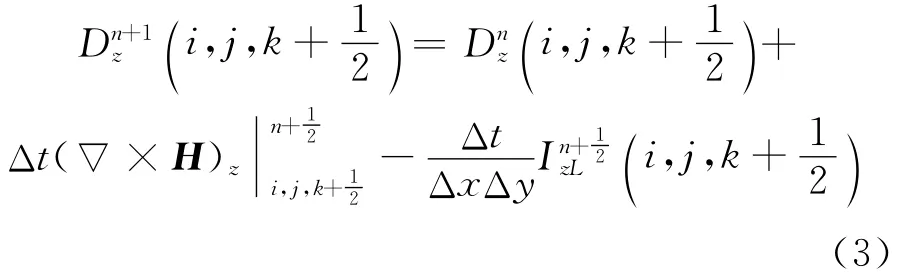
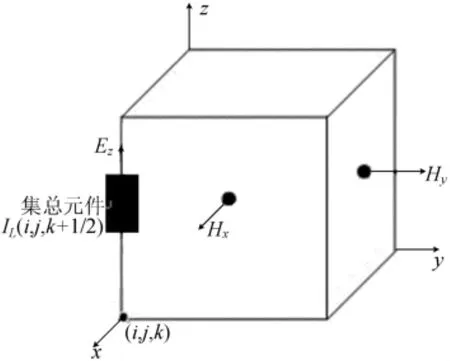
图1 集总元件位置图

不同的集总元件，其上I－V的关系不同，据此推导出各种集总元件的迭代公式如下。

电阻：

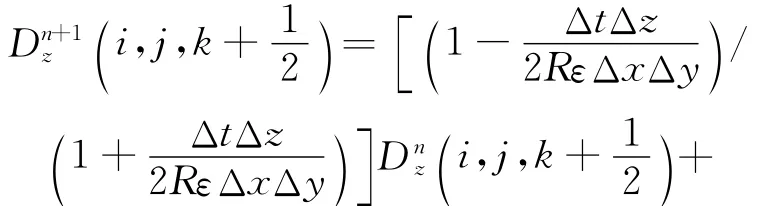
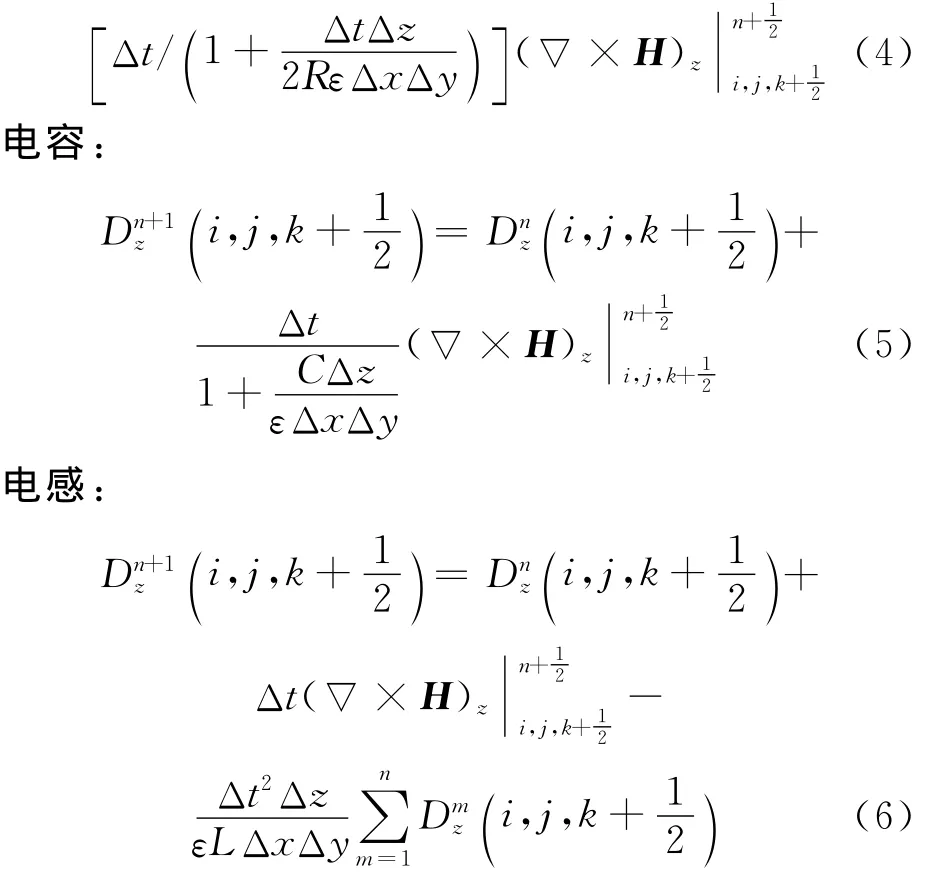
当位于Ez处的集总元件为二极管时，二极管两端的电流为：

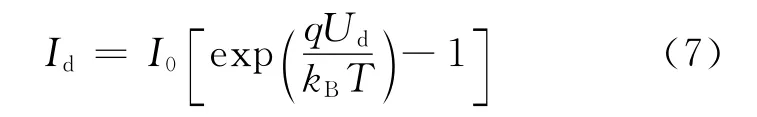
其中，q为电子电量；Ud为二极管2端电压；kB为玻尔兹曼常数；T为绝对温度。离散后代入（2）式可得：

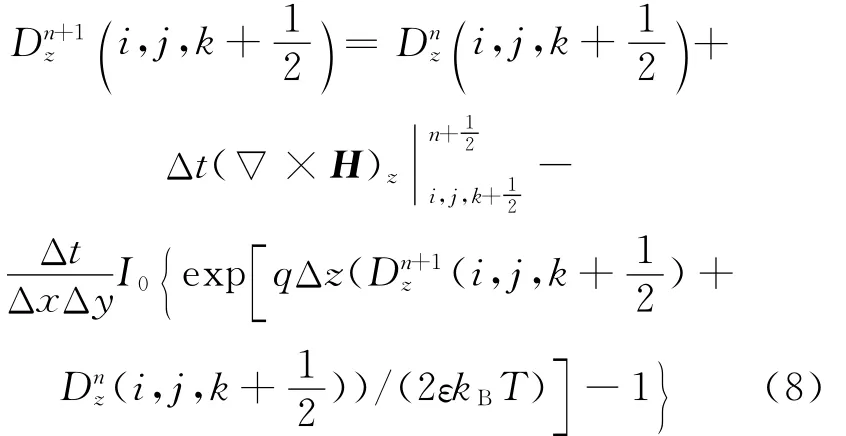
由于二极管的非线性特性，（8）式为超越方程，可以用牛顿迭代法求解出Dz在n＋1时刻的值。

2 计算实例及仿真结果

图2所示为二极管后接一个低通滤波网络构成的单管混频器，电路中介质板相对介电常数εr＝9，厚度H＝0.2536mm，微带宽W＝0.2664mm，长L1＝3mm，L2＝L3＝2mm，D为理想二极管，I0＝0.01pA，电感L＝32nH，电容C1＝C2＝6.37pF，负载R1＝50Ω。

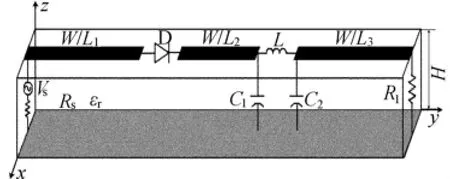
图2 单管混频器电路结构图

下面通过模拟这个非线性混合电路来验证所述方法的可行性。

电路中激励源选用的电压源Vs为2个频率的正弦波的叠加，Vs＝10sin（2πf1t）＋10sin（2πf2t），内阻Rs＝50Ω，取f1＝1.0GHz，f2＝0.9GHz，FDTD计算网格为34×100×20，网格大小Δx＝0.0444mm，Δy＝0.1000mm，Δz＝0.0634mm，时间步长Δt＝0.1ps。图3所示为不同时刻微带电路所在平面电场Ez的分布情况。

图3a所示为t＝17ps时，电磁波开始从电源端向第1个微带贴片传播；图3b所示为t＝130ps时，电磁波经由第1块贴片传播到了二极管处；图3c所示为t＝850ps时，电磁波通过了第2块贴片到达电容电感组成的滤波网络；图3d所示为t＝4.5ns时，电磁波已经传播到整个电路，达到稳态。

图4所示为二极管D两端电压VD与负载R1两端电压VR1的波形曲线，实线为FDTD的模拟结果，虚线为ADS的仿真结果。

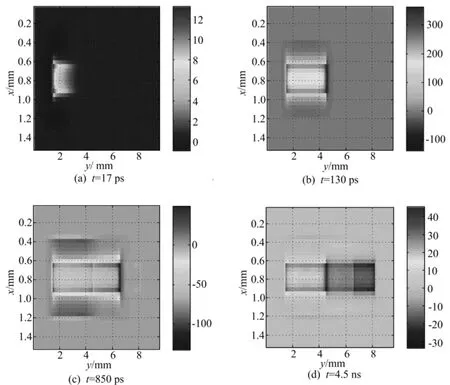
图3 微带电路所在平面Ez分布情况

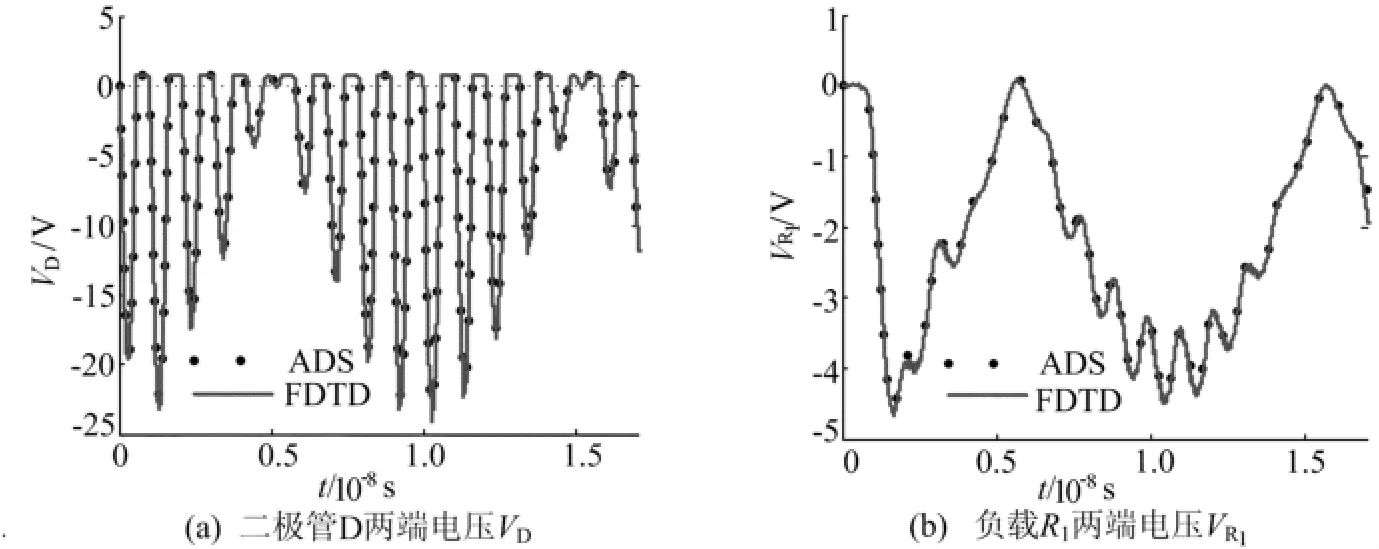
图4 FDTD与ADS对VD和VR1的仿真结果对比

从图4可以清楚看到电路已呈现出混频的效果，2条曲线几乎完全吻合，即FDTD计算结果与ADS仿真保持了高度的一致。这说明了FDTD在仿真非线性微带电路上的有效性和精确性，所得时域电磁场分布图对研究高频混合电路的电磁兼容等问题提供了重要的依据。

3 结束语

本文基于FDTD对非线性混合电路进行了全波分析，模拟结果与ADS软件仿真结果一致，证明了该方法的正确性。此方法可进行全频带模拟，并能观测到高频时电路上电磁场分布情况，得到时域场值。该方法为研究电磁兼容及串扰等问题提供了很好的依据。

［1］Yee K S.Numerical solution of initial boundary value problems involving Maxwell＇s equation in isotropic media［J］.IEEE Trans Antennas Propag，1966，14（5）：302－307.

［2］Taflove A，Brodwin M E.Numerical solution of steady－state EM scattering problems using the time－dependent Maxwell＇s equations［J］.IEEE Trans Microwave Theory Tech，1975，23（8）：623－630.

［3］Taflove A.Application of the finite－difference time－domain method to sinusoidal steady－state electromagnetic penetration problem［J］.IEEE Trans Electromagnetic Compatibility，1980，22（3）：191－202.

［4］Sui W，Christensen D A，Durney C H.Extending the twodimensional FDTD method to hybrid electromagnetic sys－tems with active and passive lumped elements［J］.IEEE Trans Microwave Theory Tech，1992，40（4）：724－730.

［5］Tsuei S Y，Cangellaris A C，Prince J L.Rigorous electromagnetic modeling of chip－package（first－level）interconnections［J］.IEEE Trans Components，Hyrids and Manufacturing Technology，1993，16（8）：876－882.

［6］Piket－May M，Taflove A，Baron J.FD－TD modeling of digital signal propagation in 3－D circuits with passive active loads［J］.IEEE Trans Microwave Theory Tech，1994，42（8）：1514－1523.

［7］Toland B，Lin J，Houshmand B，et al.FDTD analysis of an active antenna［J］.IEEE Microwave and Guided Wave Letters，1993，3（11）：423－425.

［8］张少华，杨明武，姜万顺.微带线弧形切割传输特性的FDTD研究［J］.合肥工业大学学报：自然科学版，2011，34（5）：712－715.

［9］Su H H，Kuo C W，Kitazawa T.A novel approach for modeling diodes into FDTD method［C］／／Progress in Electromagnetics Research Symposium Proceedings，Marrakesh，2011：186－189.

［10］Gedney S D.An anisotropic perfectly matched layer－absorbing medium for the truncation of FDTD lattices［J］.IEEE Trans Antennas Propag，1966，44（12）：1630－1639.