低信噪比高动态条件下基于FFT的二维平移累加PN码捕获算法

郭道省,郭文韬,秦 勇,徐 力,杨茂强

(1.解放军理工大学通信工程学院 卫星通信系,南京 210007;2.解放军92497部队 70分队,海南 陵水572425)

1 引 言

直接序列扩频(DSSS)信号被广泛应用于各种通信环境,因此直扩信号接收机在各种条件下的同步技术成为近年来研究的热点问题。同步技术包括PN码同步与载波同步,而PN码同步又分为PN码捕获与码跟踪技术。本文主要探讨及研究PN码捕获技术。关于PN码捕获技术,近年来主要从两方面考虑进行研究。

一方面是研究适应高动态DSSS信号的PN码捕获技术。其典型的应用环境为机载、弹载或LEO星载卫星导航定位。相应的码捕获技术为文献[1-2]提出的基于FFT的串并搜索的部分相关的码捕获技术。文献[3]在此算法的基础上,提出了基于FFT相位差修正的部分相关值作FFT的PN码捕获技术,使得载波频偏的估计精度大大提高。文献[4]也对此PN码捕获技术进行了研究。文献[5]提出了另一种适应高动态DSSS信号的PN码捕获技术,即分段相关的PN码捕获技术,然而其是以牺牲相关器输出的信噪比为代价的。文献[6]提出了基于FFT的频域相关的PN码捕获技术,此算法也是近年来研究最多的算法之一。文献[7]也对此算法进行了研究,并利用真实GPS信号验证了算法的有效性。文献[8]考虑能用于LEO卫星移动通信手持机中的PN码捕获技术,提出了基于滑动相关的利用码频频偏的“循环环”的PN码捕获技术,此算法的效率与码频频偏的大小有关,当码频频偏较大时,其能快速捕获信号,而当码频频偏较小时,由于滑动相关器输出相关峰的周期变大,从而使得PN码捕获的速度下降。

另一方面,低信噪比的弱DSSS信号的PN码捕获技术也是近年来研究的热点。此时信号强度一般只有-180 dBW左右,远小于正常接收时的-160 dBW。文献[9]研究了基于分段相关-视频累积的多驻留PN码捕获技术,当多普勒频偏较大且信噪比很低时,此捕获技术的性能将大大下降。文献[10]对现有的弱卫星导航信号的捕获技术进行了总结。文献[11]提出了一种基于辅助数据的载波频偏及其不确定度估计算法。

然而,上述诸多种PN码捕获技术,要么只能适应信噪比较高的高动态环境,要么只能适应于静态或低动态的弱信号环境。本文将重点研究适应低信噪比高动态环境的弱DSSS信号的PN码捕获技术,并使得此种捕获技术能适应各种应用环境,其典型的应用为GEO、HEO卫星的定轨。文献[12]研究了载波频偏及码频频偏同时存在时的PN码捕获技术,其采用了最大似然法对信号进行捕获,因此算法的运算量极大。文献[13]同时考虑载波频偏及码频频偏对相关器的影响,提出了将时移短时相关法用于PN码捕获的思想,与文献[12]中的算法相比,其运算量大大减小了。然而,文献[13]中仅考虑了载波频偏及码频频偏为常数的情况,而高动态环境下,载体加速度的存在,使得接收信号存在载波频偏变化率及码频频偏变化率,因此有必要研究此种条件下的PN码捕获技术。

2 载波频偏及码频频偏对PN码捕获的影响

以卫星导航系统为例进行分析。造成载波频偏及码频频偏的原因包括3个方面,分别为卫星与接收机相对运动造成的多普勒频偏、接收机时钟抖动与卫星星钟抖动,后两者较前者相比较小,在高动态环境下,将主要考虑多普勒频偏对PN码捕获的影响。以下分别分析由于多普勒频移造成的载波频偏及码频频偏对码捕获的影响。

2.1 载波频偏对捕获的影响

在高动态环境下,载波频偏随时间变化,表示为fd(t),将其进行泰勒级数展开,则表示为

式中,fd为常数项载波频偏,fd-rate为fd(t)的一阶导数,表示载波频偏的变化率,通常情况下 fd(t)的二阶以上导数很小,这里不予考虑。重点研究 fd与fd-rate对PN码捕获的影响。

文献[1-4]都对常数项载波频偏 fd对捕获的影响进行了分析,表明在相干累加长度一定时,相关峰会随着fd的增大而减小,当 fd增大为相干累加时间的倒数时,相关峰值将下降为零。

fd-rate为载波频偏变化率,若捕获采用具有频域扫频技术的频域相关法时,则由于fd-rate的存在,会使得相关峰向相邻的扫频间隔移动。在低信噪比高动态的弱信号环境下,为了提高检测概率,必须对相关值进行长相干累加与非相干累加,然而,由于相关峰随时间在扫频间隔的移动,因此相关峰出现在同一扫频间隔的数量有限,这将大大降低非相干累加的次数。

2.2 码频频偏对捕获系统的影响

在高动态环境下,将时变的码频频偏表示为

式中,Dc为常数项码频频偏,Dc-rate表示码频频偏的变化率,对于Dc(t)的二阶以上的导数不予考虑。

文献[8]与文献[13]研究了码频频偏对相关值的影响,表明码频频偏会使得接收信号与本地伪码的相位差发生固定的相对变化,从而导致相关峰向相邻搜索的码相位进行移动,使得相关峰在同一码相位出现的个数大大减小,因此使得非相干累加的数目下降。

当考虑码频频偏变化率Dc-rate时,将会导致接收信号与本地伪码的相位差发生时变的相对变化,导致在同一码相位相关峰出现的个数随时间变化,因此使得非相干累加的次数发生变化。如图1所示,Δt1时间段,在码相位 τ2上出现4次相关峰,由于Dc-rate的存在,码频频偏发生变化,使得在Δt2时间段,相关峰向码相位 τ3移动,且在 τ3上相关峰出现的次数变为3次。

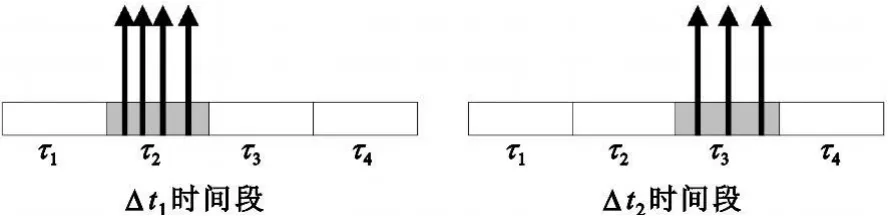
图1 时变的码频频偏造成的相关峰“漂移”现象Fig.1 Phenomenon of correlation peaks drift created by changing code frequency offset

当同时考虑载波频偏变化率与码频频偏时,将会导致相关峰同时在载波频偏不确定区与码相位不确定区移动。如图2所示,在t1时刻,相关峰出现在1号搜索单元,随着时间的变化,由于载波频偏变化率及码频频偏的影响,在 t2时刻,相关峰将出现在2号搜索单元。

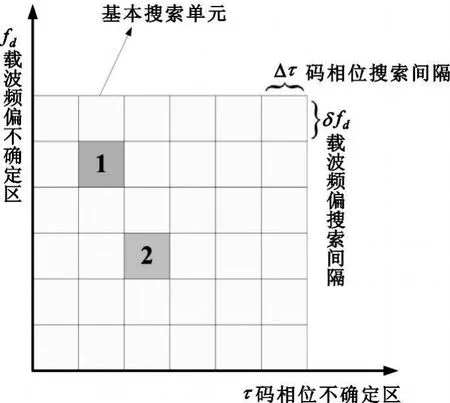
图2 相关峰在二维不确定区的移动Fig.2Movemen of correlation peaks in two-dimensional uncertainty region

为了解决载波频偏变化率与码频频偏对PN码捕获的影响,本文提出了基于FFT的二维平移累加算法。

3 基于FFT的二维平移累加算法

算法的基本思想是对相关器输出的相关值在载波频偏不确定度与码相位不确定度同时进行平移,从而消除相关峰“漂移”现象,增大非相干累加的有效性。下面对算法进行详细描述。

为消除载波频偏变化率的影响,将载波频偏变化率的不确定区Δfd-rate分为若干个搜索间隔,间隔大小为 δ fd-rate,而载波频偏的搜索间隔为 δ fd。若当前载波频偏搜索间隔的相关峰为Cpeak1,当载波频偏变化率的搜索值为fd-rate-1,经过时间ΔT,载波频偏改变fd-rate-1ΔT,相关峰将“漂移”到相邻的载波频偏搜索间隔即为Cpeak2,那么,进行非相干累加时,应将相邻载波频偏搜索间隔的相关峰值Cpeak2平移到当前载波频偏搜索间隔,平方后与当前载波频偏搜索间隔的相关值Cpeak1相累加,得到经过时间 2ΔT,载波频偏改变2fd-rate-1ΔT,相关峰将“漂移”到下面第二个载波频偏搜索间隔即为Cpeak3,则将下面第二个载波频偏搜索间隔的相关峰值Cpeak3平移到当前载波频偏搜索间隔,平方后与相累加,得到以此类推,若经过时间N·ΔT,则将下面第N个载波频偏搜索间隔的相关峰值CpeakN平移到当前搜索间隔,平方后与相累加,从而实现了N次非相干累加。在实际的PN码捕获系统中,要搜索的载波频偏变化率的值为因此要对Nfd-rate个所搜索的载波频偏变化率的估计值都要进行以上处理,最大的信噪比值将出现在与 fd-rate最接近的载波频偏变化率估计值上。

为了消除码频频偏及其变化率的影响,算法采用了载波频偏辅助码频频偏的估计方法,即若当前搜索的载波频偏及其变化率为fd-1与fd-rate-1,则相应搜索的码频频偏及其变化率为Dc-1=fd-1·Rc/fRF与Dc-rate-1=fd-rate-1·Rc/fRF,其中 Rc表示码片速率,fRF表示射频信号的频率。假定PN码捕获采用频域相关法,则要搜索的码频频偏及其变化率的值为Dc-1与Dc-rate-1,经过 ΔT1时间段,接收信号与本地伪码的相位差改变此时,相关峰将“漂移”到下一个码相位搜索间隔,则进行非相干累加时,将下一个码相位搜索间隔的相关峰平移到当前码相位搜索间隔,平方后与当前码相位搜索间隔的相关峰进行累加。以此类推,当经过ΔTN时间段,接收信号与本地伪码相位差改变此时,相关峰“漂移”到下面第N个码相位搜索间隔,则将此码相位的相关峰平移到当前搜索码相位,平方后与当前累加值进行累加。在实际码捕获时,则要对所有{Dc-i,的组合利用上述算法。

为了同时消除载波频偏变化率与码频频偏的影响,基于FFT的二维平移累加算法将同时利用上述策略对相关值在载波频偏不确定区与码相位不确定区进行平移到当前载波频偏搜索间隔与码相位搜索间隔,平方后与当前搜索单元的值进行累加,从而完成非相干累加。图3是采用基于FFT的二维平移累加算法提高非相干累加有效性示意图。

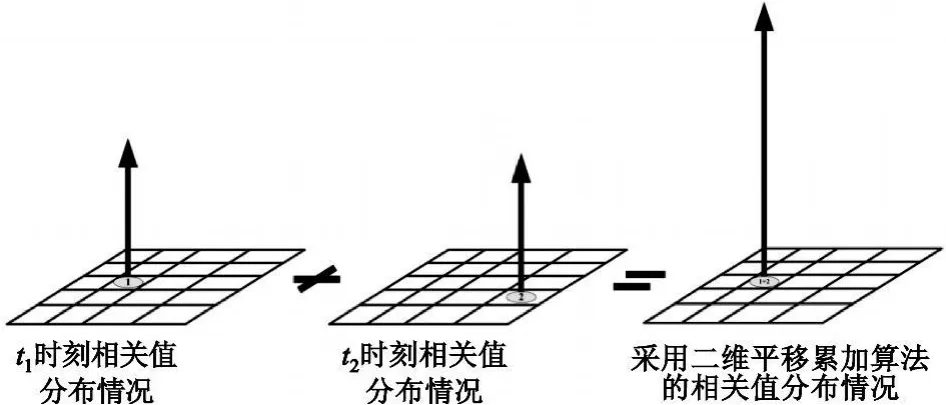
图3 基于FFT的二维平移累加示意Fig.3 Two-dimensional shift accumulation algorithm based on FFT

由图3可见,若 t1时刻在1号搜索单元出现相关峰,由于受载波频偏变化率及码频频偏的影响,t2时刻相关峰将“漂移”到2号搜索单元,基于FFT的二维平移累加算法则将2号搜索单元的相关峰平移到1号搜索单元,并与1号搜索单元的相关峰累加。

4 高动态弱信号条件下PN码捕获系统的结构图

图4是高动态弱信号条件下码捕获系统的结构图。

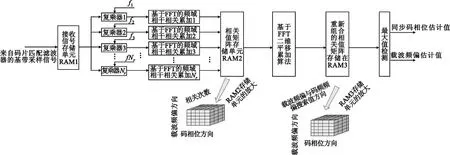
图4 高动态弱信号条件下PN码捕获的结构Fig.4 Structure diagram of PN code acquisition system for high dynamic weak signal

捕获系统工作过程:取若干秒来自码片匹配滤波器的复基带采样信号,并将其存储在接收信号存储单元RAM1中,经NT个复乘器进行时域扫频,将NT路经时域校频的数据与本地PN码在NT个并行的基于FFT的频域相干相关累加器中进行相关运算,得到相关值矩阵,并存储在RAM2中,接着,利用基于FFT的二维平移累加算法对RAM2中的相关值矩阵进行处理及重新组合,并将结果存储在RAM3中,最后进行最大值检测,从而估计出同步码相位与载波频偏。

在此码捕获结构图中,基于FFT的频域相干相关累加模块十分重要,其结构如图5所示。

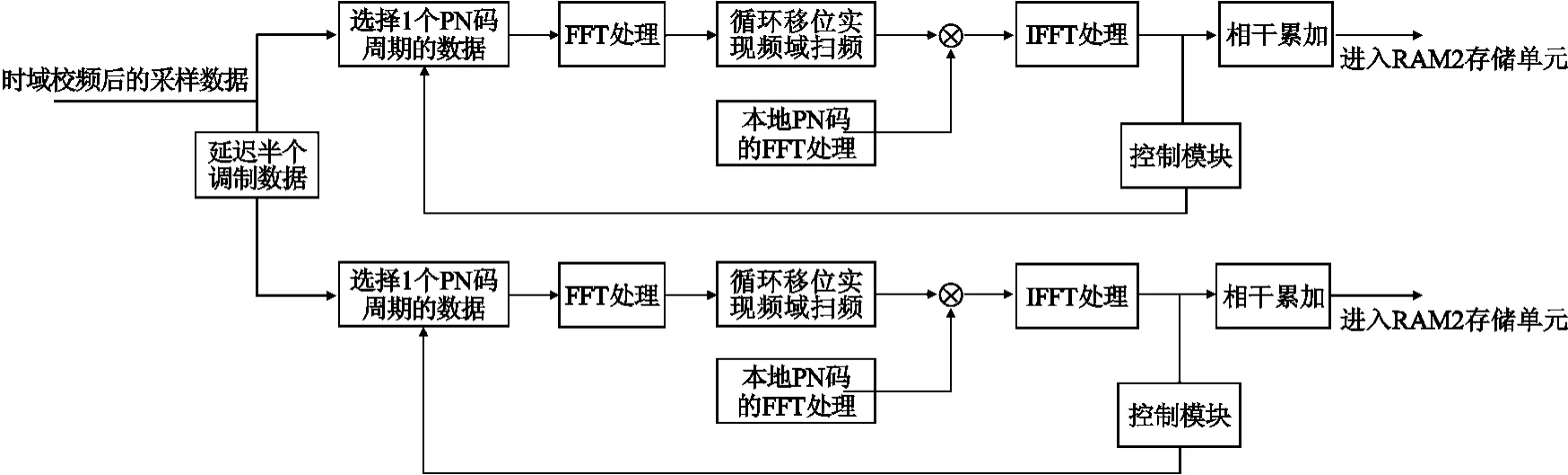
图5 基于FFT的频域相干相关累加模块结构Fig.5 Structure diagram of frequency domain coherent accumulation module

为了消除调制数据跳变对PN码捕获的影响,采用文献[14]中提出的交替的半个数据位选取技术,图5中经时域校频后的数据分为两路,一路直接进行相关处理,另一路则延迟半个调制数据位再进行相关处理。在相关处理时,首先选取1个PN码周期的采样数据进行FFT处理,并对FFT结果进行循环移位,从而实现频域扫频,将其与本地PN码FFT的结果相乘,再作IFFT,得到相关运算的结果。通过控制电路,选取新的1个PN码周期的数据,重复以上操作,并与上次同扫频间隔同码相位搜索间隔所得相关值相累加,实现相干累加,并将相关值矩阵存储在RAM2中。

由于频域扫频只能消除整数倍fs/NFFT的载波频偏,NFFT为FFT点数,fs为采样频率,因此要消除小于fs/NFFT的载波频偏,必须利用时域扫频,此为图4中存在NT个并行的时域扫频因子的原因。

5 关键参数分析

以下以GPS民用导航信号为例,对捕获系统的重要参数进行分析,包括相干累加长度、非相干累加次数、载波频偏搜索间隔、载波频偏变化率搜索间隔、码频频偏的搜索及对捕获处理速度的要求。

5.1 相干累加长度的优化

相干累加长度越大,相关器输出的信噪比越高,然而,受导航电文跳变的影响,对于GPS C/A码信号而言,相干累加长度最大为20 ms。在实际信号捕获时,20 ms内可能存在比特跳变,因此为了保证相干累加长度内没有比特跳变,将20 ms的数据分为两个10 ms,分别进行相干相关处理,从而保证其中一个相关值不存在比特跳变。若10 ms相干长度不能满足对信噪比的要求,可以通过对导航电文的预测消除导航电文的影响,进而增大相干累加长度。

5.2 非相干累加次数的优化

高动态弱信号条件下,采用非相干累加,在对抗载波频偏与导航电文跳变的同时可以增大相关器输出的信噪比,从而提高检测概率。分析同步单元与非同步单元相关值的概率分布情况,检测概率即为同步单元相关值大于所有非同步单元相关值的最大值的概率。当检测概率给定时,通过概率计算可以得到所要求的非相干累加次数。

5.3 载波频偏搜索间隔的选取

当载波频偏位于两个搜索单元中间时,由于估计误差的原因,相关峰会下降。经计算,当载波频偏估计误差为相干累加时间倒数的1/4时,相关峰能量损失0.9 dB,估计误差为相干累加时间倒数的1/2时,相关峰能量损失4 dB,因此将载波频偏搜索间隔选为相干累加时间倒数的1/2。对于GPS信号而言,若相干累加时间为10 ms,则载波频偏搜索间隔取为50 Hz。

5.4 载波频偏变化率搜索间隔的选取

若真实的载波频偏变化率位于两个搜索单元中间时,应用基于FFT的二维平移累加算法,对相关值在载波频偏不确定区进行平移时,将出现最大载波频偏补偿误差,因此要求在整个非相干累加时间内,由于载波频偏变化率估计误差导致的相关峰“漂移”不大于半个载波频偏搜索间隔,对于GPS民用导航信号而言,若进行100次非相干累加,即非相干时间为2 s,则要求载波频偏变化率搜索间隔小于25 Hz,此处取为10 Hz。

由于采用了载波频偏辅助的码频频偏搜索策略,因此对于码频频偏及其变化率的搜索由载波频偏及其变化率搜索而定。

5.5 对捕获速度的要求

由于载波频偏与码频频偏补偿误差的存在,导致捕获完成后所估计的载波频偏及同步码相位与真实值有差异,为了保证捕获成功,要求差异分别小于半个载波频偏搜索间隔和半个码片宽度。若载波频偏变化率的搜索间隔为10 Hz,则最大估计误差为5 Hz,要满足上述要求即在整个捕获期间由于载波频偏变化率估计误差导致的载波频偏改变小于25Hz,捕获必须在5 s内完成。目前FPGA或DSP器件的速度很难达到此要求,因此有必要进行二次搜索。

6 算法性能仿真

以下将通过MATLAB仿真对基于FFT的二维平移累加算法的检测概率进行分析。仿真条件:GPS在L1载频(1 575.42MHz)的民用导航信号,PN码周期为1 023,码片速率为1.023 Mchip/s,相干相关时间为10 ms,载波频偏范围是-10～10 kHz,码频频偏范围是-10～10 Hz,载波频偏变化率范围是-1～1 kHz,载波频偏搜索间隔为50 Hz,码频频偏搜索间隔为0.5 Hz,载波频偏变化率搜索间隔为50 Hz。

图6和图7分别是捕获系统采用最大值检测法,一般非相干累加码技术与采用基于FFT的二维平移累加算法的检测概率。由图6可见,随着非相干累加次数Q的增大,检测概率反而出现急剧下降的情况。其原因是由于码频频偏造成的,当码频频偏为10 Hz时,非相干累加的有效次数最多为10次,当非相干累加为20次,相关峰将漂移到相邻码相位,使得在两个搜索码相位出现相关峰,导致同步码相位的检测概率下降;当非相干累加次数更大时,相关峰将出现在多个搜索码相位,检测概率将进一步下降,图6中Q为30的检测概率比Q为20时更低。由图7可知,采用基于FFT的二维平移累加算法,检测概率会随 Q的增大显著提高。图7中,Q为30、载噪比 C/No为24 dB时,检测概率已达到0.996,而图6中 Q为30时,检测概率已降到0.2以下,与图6中 Q为10时的检测概率相比有2 dB增益;图7中 Q为 100、载噪比 C/No为21 dB时,检测概率已达到0.998,与图6中Q为10时的检测概率相比有6 dB增益。因此在低信噪比高动态条件下,采用基于FFT的二维平移累加算法可以大大提高捕获系统的检测概率。

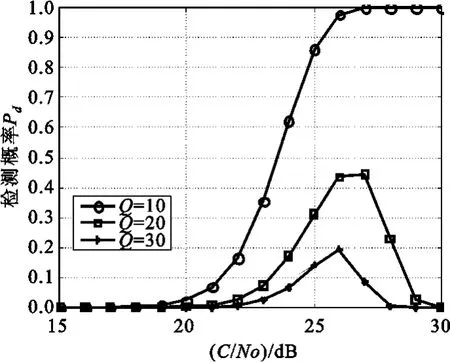
图6 采用一般非相干累加技术的检测概率曲线Fig.6 Detective probability using common noncoherent accumulation technology

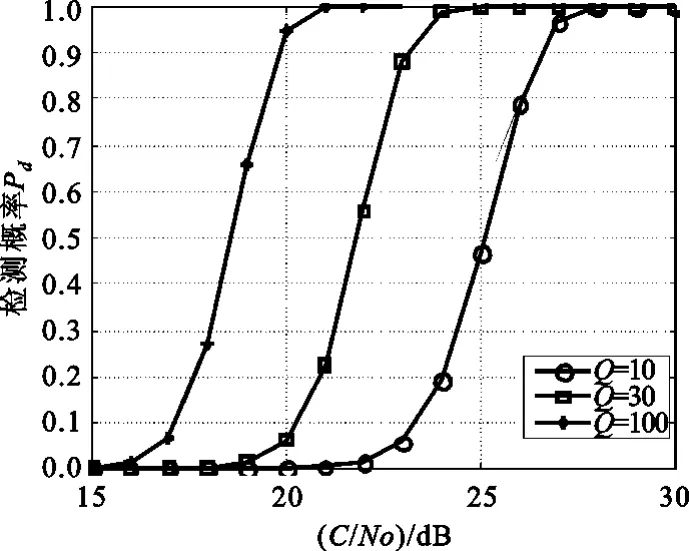
图7 采用基于FFT的二维平移累加算法的检测概率曲线Fig.7 Detective probability using two-dimensional shift accumulation algorithm based on FFT

7 结束语

本文对现有PN码捕获技术进行了总结,分析了低信噪比高动态弱DSSS信号条件下时变的载波频偏与码频频偏对PN码捕获的影响,在此基础上,提出了基于FFT的二维平移累加算法,从而提高了非相干累加的有效性,给出了捕获系统结构图,并对关键参数的选择进行了分析,通过MATLAB仿真证实了算法的有效性。对算法的运算量进行评估与优化,论证利用FPGA或DSP实现的可行性将是下一步的研究内容。最后,建议将一些辅助信息与此算法相结合,可大大压缩搜索空间,增强低信噪比高动态弱DSSS信号的捕获能力。

[1]Sascha M S,Gordon J R P.Code acquisition for LEO satellite mobile communication using a serial-parallel correlator with FFT for Doppler estimation[J].IEEE Transactions on Vehicular Technology,2001,50(6):1549-1567.

[2]Candida L S,Sascha M S,Gordon J R P.Aserial-parallel FFT correlator for PN code acquisition from LEO satellites[C]//Proceedings of 1998 IEEE International Symposium on Spread Spectrum Techniques and Applications.Sun City,South Africa:IEEE,1998:446-448.

[3]郭飞,朱文明,李志强,等.基于FFT相位差修正的伪码快捕方法[J].无线电通信技术,2006,32(2):15-17.GUO Fei,ZHU Wen-ming,LI Zhi-qiang,et al.Fast code acquisition based on phase difference correction of FFT[J].Radio Communications Technology,2006,32(2):15-17.(in Chinese)

[4]秦勇,张邦宁,郭道省.大频偏下直接序列扩频系统的码捕获技术[J].无线通信技术,2005,14(4):18-21.QIN Yong,ZHANG Bang-ning,GUO Dao-xing.Code acquisition technique of DS/SS with large frequency offset[J].Wireless CommunicationTechnology,2005,14(4):18-21.(in Chinese)

[5]Persson B,DoddsD E,Bolton R J.A segmented matched filter for CD MA code synchronizationin systemswithDoppler frequency offset[C]//Proceedings of IEEE Global Telecommunication Conference.San Antonio,Texas:IEEE,2001:648-653.

[6]Vannee D J R,Coenen A J R M.New fast GPS code acquisition technique using FFT[J].Electornics Letters,1991,27(17):158-160.

[7]刘晓莉,李云荣.一种基于FFT的高动态GPS信号快速捕获方法[J].系统仿真学报,2007,19(10):2151-2155.LIU Xiao-li,LI Yun-rong.Fast Acquisition Based on FFT for High Dynamic GPS Signals[J].Journal of System Simulation,2007,19(10):2151-2155.(in Chinese)

[8]Glisic S G,Poutanen T J,Wu W W,et al.New PN code acquisition scheme for CDMA networks with low signal-tonoise ratios[J].IEEETransactions onCommnications,1999,47(2):300-310.

[9]朱祥维,王飞雪.基于分段相关-视频积累方法的多驻留伪码捕获系统优化设计[J].通信学报,2006,27(9):124-128.ZHU Xiang-wei,WANG Fei-xue.Optimum design of multiple dwell PN code acquisition system using segment correlation-video integration method[J].Journal on Communications,2006,27(9):124-128.(in Chinese)

[10]戴卫恒,朱文明,常江,等.弱信号条件下的卫星导航技术进展[J].全球定位系统,2009(1):29-32.D AI Wei-heng,ZHU Wen-ming,CHANG Jiang,et al.Development of satellite navigation system inweak signal condition[J].GNSS World of China,2009(1):29-32.(in Chinese)

[11]宋成,王飞雪,庄钊文.辅助型GPS接收机中载波频偏及其不确定度估计算法的研究[J].信号处理,2009,25(11):1694-1700.SONG Cheng,WANG Fei-xue,ZHANG Zhao-wen.An estimate algorithm for carrier frequency shift and Its uncertainty in the assisted GPS receiver[J].Signal Processing,2009,25(11):1694-1700.(in Chinese)

[12]Cheng Unjeng,HurdW J.Spread spectrum code acquisitionin the presence of Doppler shift and data modulation[J].IEEE Transactions onCommnications,1990,38(2):241-250.

[13]秦勇,张邦宁,郭道省.时移短时相关法在DSSS码捕获系统中的应用[J].电子与信息学报,2007,29(8):1942-1945.QIN Yong,ZHANG Bang-ning,GUO Dao-xing.Application of DSTC to Code Acquisition System of DSSS[J].Journal of Electronics&Information Technology,2007,29(8):1942-1945.(in Chinese)

[14]Mark L,Psiaki.Block acquisition of weak GPS signal in a software receiver[C]//Proceedings of Institute of Navigation GPS.Salt Lake City,Utah:ION,2001:2838-2850.