Hilbert-Huang算法研究

樊迎迎，刘卓夫，汤泰青

（哈尔滨理工大学 通信工程系，黑龙江 哈尔滨 150080）

Hilbert-Huang算法研究

樊迎迎，刘卓夫，汤泰青

（哈尔滨理工大学 通信工程系，黑龙江 哈尔滨 150080）

非线性、非平稳信号处理一直是热点问题。Hilbert-Huang变换是一种新的信号处理方法，它通过经验模态分解EMD算法和Hilbert变换能够得到信号的时间-频率-能量分布特征。但其在应用中，处理结果精确度不高。基于提高Hilbert-Huang变换的处理结果的精确度，提出了一些改进方法，通过MATLAB进行仿真，验证了改进方法的可行性及有效性。

Hilbert-Huang变换；经验模态分解；固有模态函数；曲线拟合

生活中存在很多非线性、非平稳信号需要我们对其进行处理分析，而传统的信号分析如傅立叶变换和小波分析都建立在线性、高斯性和平稳性的基础上[1]，因此它们不适合用于非平稳信号。文中介绍的希尔伯特-黄变换 （Hilbert-Huang Transform，简称HHT）是一种全新的信号处理方法，对于处理非线性、非平稳信号有清晰的物理意义，能够得到信号的时间-频率-能量分布特征，且是一种自适应性的信号处理方法[2]。

1 HHT基本原理

1.1 EMD基本原理方法

EMD的基本原理和算法描述如下。

1.1.1 本征模态函数（IMF）定义

本征模态函数必须满足以下2个条件[3]:

1）在全局特性上看，整个数据的极值点数和过零点数相差不能超过一个；

2）在局部特性上看，任意数据点处由局部极大值点定义的包络线和局部极小值定义的包络线的均值都为0。

1.1.2 经验模态分解方法

经验模态分解（EMD）：假设任何信号都可以由一系列的IMF所组成，这些IMF表征着信号的内在波动特征。EMD过程就是将非线性不平稳信号由高频到低频分解成若干个IMF的过程，并且每个IMF的频率分辨率也是随着原始信号的变化而变化，是一种自适应的信号处理方法。

对信号x（t），其信号分解过程[4]为：

1）首先求出序列x（t）所有的极大值点和极小值点，再利用三次样条曲线进行插值拟合，得到数据的上、下包络线，并计算出上、下包络线的均值m1，从而求出原始数据序列x（t）和包络均值的差值h1=x（t）-m1。

2）判断h1是不是IMF，如果不是则对其重复上述过程，直到第k次的h1k为IMF，令c1=k1k，c1为从原始数据中提取出来的第1个IMF，包括信号的最高频率成分。

3）求出原数据x（t）与第 1 个 IMFc1的差值r1=x（t）-c1，将r1作为新数据序列重复上述过程，可以递推得到其他IMF，直至趋势分量rn单调或只有一个极值。

4）原数据序列最终可分解为：

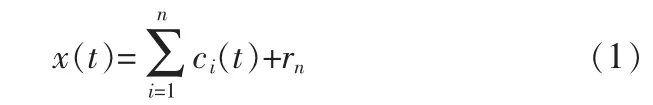
其中rn为趋势分量，为单调函数或均值函数，代表信号的平稳趋势；c1，c2，…，cn为所得到的各个IMF分量，包含了信号由高频到低频段的不同成分。

1.2 HHT时频分析方法

HHT处理非平稳信号的过程包含了上述EMD分解过程，并且进一步将由EMD分解得到的每一个IMF进行Hilbert变换，从而形成原始信号的Hilbert谱。具体如下：

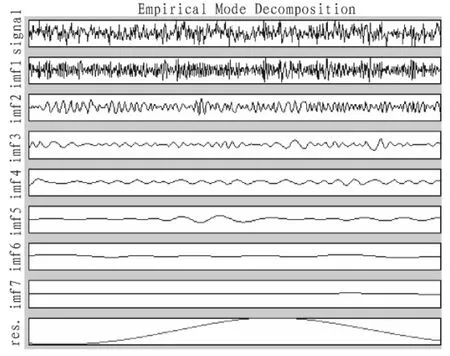
图1 由EMD法分解的仿真信号的IMFFig.1 IMF of the simulated signal through empirical mode decomposition

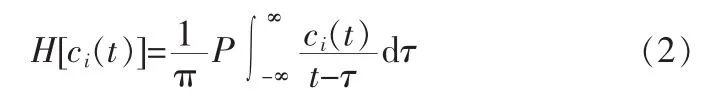
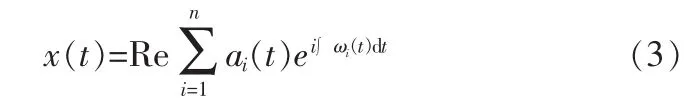
式中，Re表示取实部。

式（3）中每个分量的幅值和相位都是随时间变化的时间函数。式（3）的右部称为信号x（t）的Hilbert时频表示，记为：

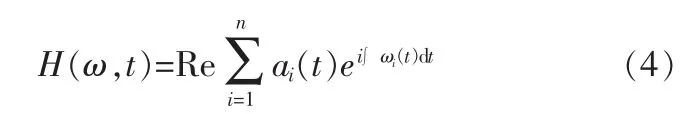
应用式（4）可以将信号的时间-频率-幅值的三维关系表达出来。

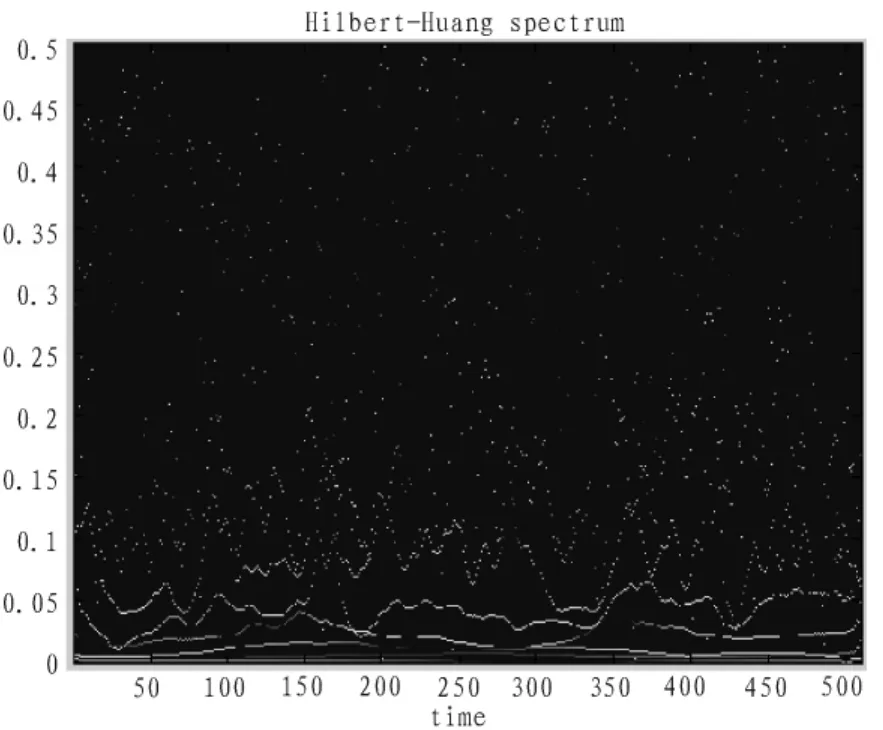
图2 仿真信号的Hilbert谱图Fig.2 Hilbert spectrum of the simulated signal

上述EMD分解和对应的Hilbert变换统称为Hilbert-Huang变换。

2 HHT的问题及改进

2.1 拟合方法的改进

从前文介绍的EMD方法认识到，拟合方法对求取包络线有着重要影响，通过极值点拟合上下包络线，进而求均值线的步骤是分解的基础，也是整个HHT的起始，这个过程决定着HHT分析结果的可信程度。

HHT的发明者Huang使用了三次样条拟合法进行包络线拟合，但在实验过程中发现三次样条拟合法虽然光滑性很好[5]，但容易造成过冲和欠冲现象，如图3所示。为了克服三次样条拟合的缺点，我们需要选择其他拟合方法来生成上、下包络线，B样条拟合函数有许多样条函数没有的优点[4]，如移动某个节点只会影响临近的几段曲线，便于对生成的曲线进行局部修改，可以灵活地构造成任意形状的曲线等。因而应用B样条拟合法，符合EMD方法的初衷：非线性信号的局部化处理。

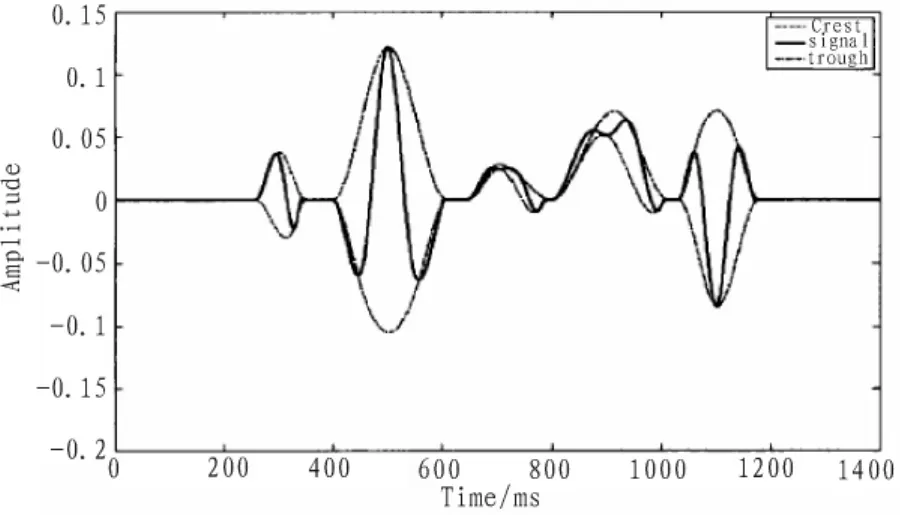
图3 三次样条拟合过冲或欠冲的表现Fig.3 Appearance of overshoot and undershoot of the three times spline curve fitting

2.2 边界效应

HHT的核心是EMD。每个IMF都需要经多次筛选来实现，而每次筛选必须找到局部极值点构成的包络线并用插值法来计算出上下包络的平均值。因为信号端点一般不会是局部极值点，所以必须对信号进行外延，以确保包络线能够抵达端点。包络线外延不准确会引起误差，而这种误差会随着IMF分解个数的增加而向内传播，继而污染整个序列，使得最后的分解结果失去意义。尽管Huang宣称解决了边界问题，但他同时也指出，EMD方法面临的边界问题还没完全解决，因此解决边界问题对于HHT的理论研究具有重要意义。

目前主要的边界处理方法有：线性外拓法；多项式拟合法；神经网络预测方法及端点镜像方法。

胡维平[6]对这些方法做了比较和总结：线性外拓法尽管比较粗糙，但它在处理随机信号和渐变准周期信号时优于多项式拟合法，鉴于该算法的简单高效，可以在实时处理的场合得到应用；多项式延拓在处理准周期信号时比较出色，但在随机信号上相对较差，这说明多项式法的EMD并不适用于无规律的信号处理；神经网络算法由于其预测信号序列方法的局限性，预测的准确度与预测的长度成反比，以及对随机信号准确预测的困难性，因此无论是处理随机信号还是渐变准周期信号都与镜像算法有一定的差距；而镜像法无论在随机信号还是在准周期信号中都以较明显的优势成为首选。因为对于长短周期信号来说，镜像法基本上都能够很好的保留边界上的信号特征，在准周期信号和随机信号的处理中都具有很好的作用。

3 结 论

文中基于提高Hilbert-Huang变换的处理结果精度，提出了对EMD算法的改进，通过MATLAB仿真比较各种算法，找到了最合适的算法，解决了Hilbert-Huang算法处理精确度不高的问题。

[1]刘鲁源，李宗勃.从傅里叶变换到小波变换[J].自动化与仪表，2000（6）:18-23.

LIU Lu-yuan，LI Zong-bo.From Fourier transform to wavelet[J].Automation and Instrument，2000（6）:18-23.

[2]Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and Hilbert spectrum for nonlinear and nonstationary time series analysis[J].Pro Royal Society London A，1998：903-905.

[3]杨世锡，吴劲松，吴昭同.基于高次样条插值的经验模态分解方法研究[J].浙江大学学报，2004，38（4）:267-270.

YANG Shi-xi，WU Jin-song，WU Zhao-tong.Research on empirical mode decomposition based on high times spline fitting[J].Zhejiang University Journal，2004，38（4）:267-270.

[4]Huang N E，WU M L，QU W D，et al.Applications of Hilbert-Huang transform to non-stationary financial time series analysis[J].Applied Stochastic Models in Business and Industry,2003，19（3）:245-268.

[5]宋松.B样条插值曲线的快速算法 [J].系统工程与电子技术，1995（12）:44-52.

SONG Song.The quick algorithm of B spline[J].System Engineering and Electronic Techlogy，1995（12）:44-52.

[6]胡维平，莫家玲，龚英姬，等.经验模态分解中多种边界处理方法的比较研究 [J].电子与信息学报，2007，29（6）:1394-1398.

HU Wei-ping，MO Jia-ling，GONG Ying-ji，et al.Research on the comparison among the several boundary processing method of empirical mode decomposition[J].Electronic and Information Journal，2007，29（6）:1394-1398.

Research on Hilbert-Huang transform

FAN Ying-ying， LIU Zhuo-fu， TANG Tai-qing
（Department of Communication Engineering，Harbin University of Science and Technology，Harbin150080，China）

Nonlinear and non-stationary signal processing has been always a hot issue.Hilbert-Huang transform is a new signal processing method，which can get the time-frequency-energy distribution characteristics of the signals through the empirical mode decomposition （EMD） and Hilbert transform.But when it is in application， the results gained are not very precise，some improvements are proposed，and it proved feasibility and useful through MATLAB simulation.

Hilbert-Huang transform；empirical mode decomposition；intrinsic mode function；curve fitting

TN911.7

A

1674－6236（2012）06-0023-03

2011-12-31稿件编号：201112169

樊迎迎（1986—），女，黑龙江鸡西人，硕士。研究方向：信号与信息处理。