自适应神经模糊推理系统(ANFIS)及其仿真
2012-09-27张小娟
张小娟
(宝鸡文理学院 电子电气工程系,陕西 宝鸡 721007)
自适应神经模糊推理系统(ANFIS)及其仿真
张小娟
(宝鸡文理学院 电子电气工程系,陕西 宝鸡 721007)
以一个非线性模型为研究对象,通过对自适应神经模糊推理系统(ANFIS)建模机理的研究建立了非线性实例模糊模型,借助MATLAB中ANFIS的功能讨论隶属度函数的数目、ANFIS输出、训练误差等对自适应神经模糊推理系统(ANFIS)的影响,取得了良好的效果。结果表明利用ANFIS进行非线性系统建模和辨识是可行的,其辩识精度很高。
自适应神经模糊推理系统;非线性系统;非线性;隶属度;仿真
非线性系统建模问题是目前学术界研究的热点问题。常用的传统非线性系统描述方法有微分(或差分)法、泛函级数法、NARMAX模型法及分块系统法等。但是对于一个非线性、多变量的复杂系统,用常规的数学方法建模既费时又费力,而且在各种假设下建模,其适应性也不好。而J-S.R.Jang提出的自适应神经模糊推理系统 (Adaptive Neural—Network-Based Fuzzy Interference System,ANFIS)是一种将模糊逻辑和神经元网络有机结合的新型的模糊推理系统结构,采用反向传播算法和最小二乘法的混合算法调整前提参数和结论参数。并能自动产生If-Then规则。本文主要介绍应用ANFIS方法进行非线性系统的建模和辨识。
1 ANFIS的结构和工作原理
ANFIS是一种基于Takagi-Sugeno模型[1]的模糊推理系统,它将模糊控制的模糊化、模糊推理和反模糊化3个基本过程全部用神经网络来实现,利用神经网络的学习机制自动地从输入输出样本数据中抽取规则,构成自适应神经模糊控制器,通过离线训练和在线学习算法进行模糊推理控制规则的自调整,使其系统本身朝着自适应、自组织、自学习的方向发展。
为简单起见,假定所考虑的模糊推理系统有2个输入x和y,单个输出z。对于一阶Takagi-Sugeno模糊模型,如果具有以下2条模糊规则:
规则 1:ifxisA1andyisB1thenf1=p1x+q1y+r1;
规则 2:ifxisA2andyisB2thenf2=p2x+q2y+r2.
ANFIS结构如图1所示,图中每一层结点具有相同的函数,设层 1的第i个结点的输出为O1,i。
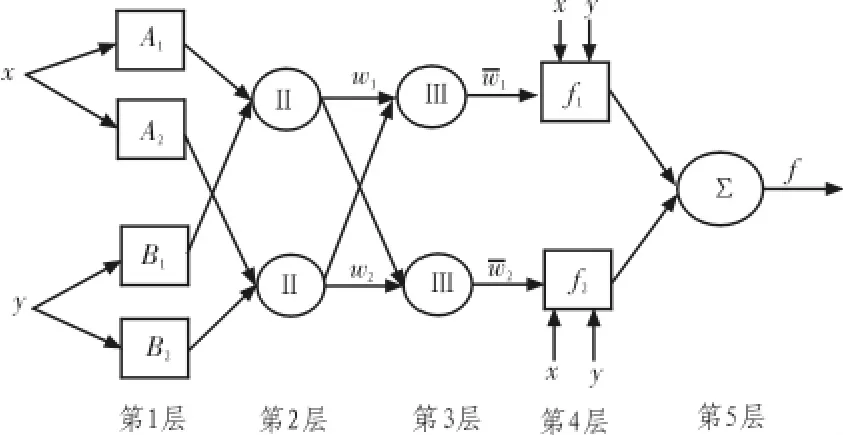
图1 ANFIS结构图Fig.1 Structure chart of ANFIS
第1层:将输入变量模糊化,输出对应模糊集的隶属度,所以可以称为模糊化层。该层的每个结点i是一个有结点函数的自适应结点。

这里x和y是结点i的输入,O1,i是模糊集A(A1,A2,B1或B2)的隶属度,A的隶属函数μA(x)可以是任意合适的参数化隶属函数,如一般的钟型函数。

式中{ai,bi,ci}是参数集,称为前提参数。当这些参数的值改变时,钟型函数也随之改变。
第2层:实现前提部分的模糊集的运算。在这一层中的每个结点都是固定结点,它的输出是所有输入信号的代数积,如下式所示:

每个结点的输出表示一条规则的激励强度,本层的结点函数还可以采用取小、有界积或强积的形式。
第3层:将各条规则的激励强度归一化,该层中的结点也是固定结点。

第4层:这一层的每个结点i是一个有结点函数的自适应结点,计算出每条规则的输出。

第5层(输出层):这一层的单结点是一个标以∑的固定结点,它计算所有传来信号之和作为总输出:
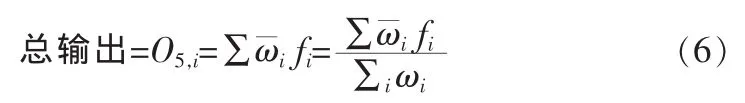
对于前提参数和结论参数,通常采用一种混合学习算法[2]进行训练。对于前提参数,采用反向传播算法,而对于结论参数则采用线性最小二乘估计算法调整参数。在每一次迭代中,首先输入信号沿网络正向传递直到第4层,此时固定前提参数,采用最小二乘估计算法调节结论参数;然后,信号继续沿网络正向传递直到输出层。此后,将获得的误差信号沿网络反向传播,从而可调节前提参数。以此方式对给定的条件参数,可以得到结论参数的全局最优点,这样不仅可以降低梯度法中搜索空间的维数,通常还可以大大提高参数的收敛速度。
一般地,在MATLAB中模糊建模的过程可分为以下步骤:
1)产生训练数据和检验数据。2)确定输入变量的隶属度函数的类型和个数。3)由genfis1函数产生初始的FIS结构。4)设定ANFIS训练参数。5)利用anfis函数训练ANFIS。6)检验得到的FIS的性能。若满足要求则认为该ANFIS系统是有效合理的基于模糊推理的系统。
2 非线性系统建模及仿真参数分析
利用模糊推理系统对下面的非线性函数[3-6]进行仿真。
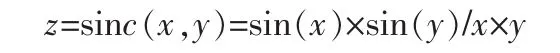
设定x,y的范围均为[-10,10],并设定每个输入模糊隶属度函数采用广义的钟形函数,训练次数为100,初始步长为0.01,得到的曲线图如图 2、3、4 所示。
在MATLAB编制程序如下:

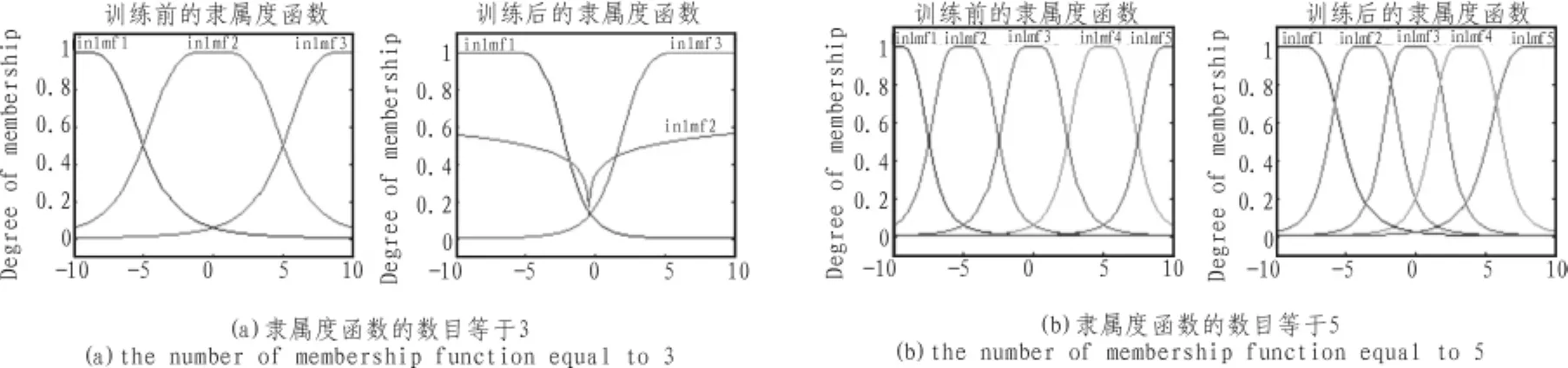
图2 ANFIS训练前后的隶属度函数Fig.2 ANFIS membership functions before and after training

图3 训练数据和ANFIS输出Fig.3 Training data and ANFIS output
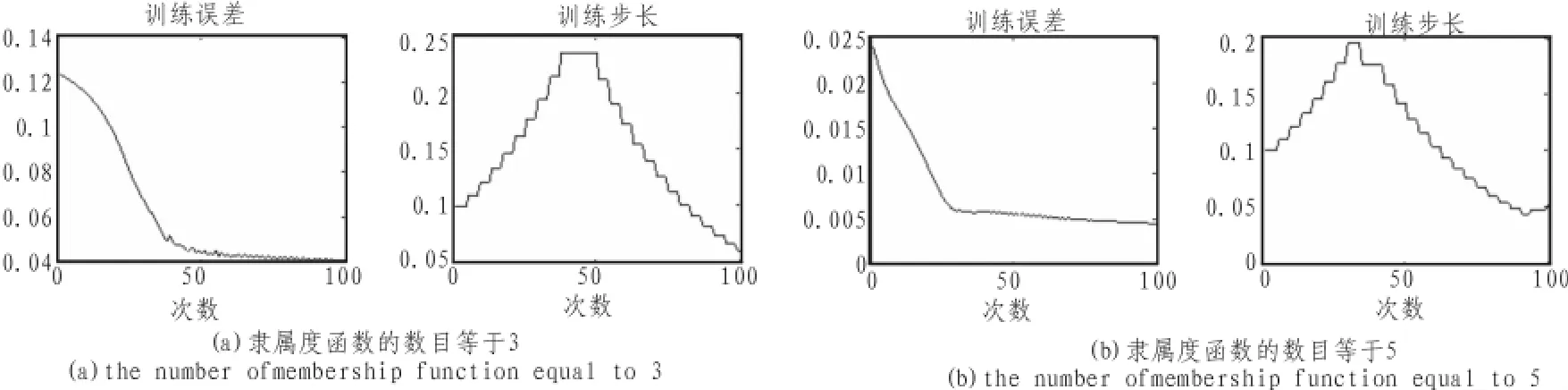
图4 训练误差和训练步长曲线Fig.4 Training error and training step curve

图 2(a)和图 2(b)的隶属度个数分别为 3 和 5,图 3(a)、图 3(b)、图 4(a)、图 4(b)分别为所对应的曲线;由图可以清楚知道逼近曲线是非常精确的,训练后的ANFIS的输出与训练数据的均方根误差RMSE分别为0.040 758 6、0.004 578 97,模型的逼程度非常好且能满足一般要求。
同时在训练过程中训练误差一直保持分别在0.123 402、0.023 964以下,随着训练次数的增多模型更加精确,实验证明在增大隶属度函数的个数或者增加训练次数的情况下,模型的精度得到进一步提高。
3 结 论
本文主要研究了非线性系统的模糊建模和仿真,借助Matlab中ANFIS的功能讨论隶属度函数的数目、ANFIS输出、训练误差等对自适应神经模糊推理系统(ANFIS)的影响,取得了良好的效果,为后续对动态非线性系统的进一步的研究打下了基础;MATLAB中ANFIS的功能实现起来比较方便也很实用,通过对ANFIS后件参数辩识的算法的改进能进一步的提高系统建模的精度和速度。自适应神经模糊推理系统(ANFIS)是模糊控制与神经网络控制的结合,在实际应用中,对于复杂系统的建模与控制提供了一个有效工具。
[1]易继锴,侯媛彬.智能控制技术[M].北京:北京工业大学出版社,2003.
[2]许丽佳,陈阳舟.基于MATLAB的非线性系统模糊建模及仿真[J].计算机仿真,2004,42(5):49-52.
XU Li-jia,CHEN Yang-zhou.Fuzzy model building and simulation for nonlinear system based on MATLAB[J].Computer Simulation,2004,42(5):49-52.
[3]叶吉祥,路秋静,唐贤瑛.基于ANFIS的微波炉温度控制[J].计算机工程与设计,2004,25(11):2119-2121.
YE Ji-xiang,LU Qiu-jing,TANG Xian-ying.Temperature control of micro-wave oven based on ANFIS[J].Computer Engineering and Design, 2004,25(11):2119-2121.
[4]秦炎峰,陈铁军.自适应神经模糊推理系统的参数优化方法[J].微计算机信息,2008(18):222-224.
QIN Yan-feng,CHEN Tie-jun.Parameters optimization methodsofadaptive neuro-fuzzy inference systems[J].Microcomputer Information,2008(18):222-224.
[5]程锋章,于希宁.非线性系统的模糊建模及仿真[J].仪器仪表用户,2005,12(6):114-115.
CHENG Feng-zhang,YU Xi-ning.Fuzzy model building and simulation for nonlinear system[J].Electronic Instrumentation Customer,2005,12(6):114-115.
[6]顾秀萍.自适应神经模糊推理系统 (ANFIS)及其仿真[J].火力与指挥控制,2010,35(2):48-53.
GU Xiu-ping.Study on the adaptive network-based fuzzy inference system and its simulation[J].Fire Control&Command Control,2010,35(2):48-53.
Study on the adaptive network-based fuzzy inference system and simulation
ZHANG Xiao-juan
(Dept.Electronics&Elect.Eng.,Baoji Coll.Arts&Sci.,Baoji721007,China)
A nonlinear example was studied,through the study of ANFIS,and corresponding fuzzy model was established.Some simulation experiments were carded on.Direct effect of adaptive network based fuzzy inference systems (ANFIS)about training errors,the number of membership functions and ANFIS output is researched by ANFIS of MATLAB,which achieves good results.The simulation results show that ANFIS is very effective to identify the nonlinear system and its accuracy is very high.
ANFIS;nonlinear system;non-linear;membership function;simulation
TP302
A
1674-6236(2012)05-0011-03
2011-12-22稿件编号:201112124
陕西省教育厅科学计划项目资助(2010JK401);宝鸡市科技局项目资助(11KG-W05);宝鸡文理学院项目资助(ZK11173)
张小娟(1978—),女,陕西永寿人,硕士,讲师。研究方向:智能控制与模式识别。
