ACPSO-SVR结合的非线性建模预测算法研究

韩晓霞，谢 刚，韩晓明，谢克明

（太原理工大学 信息工程学院，山西 太原 030024）

ACPSO-SVR结合的非线性建模预测算法研究

韩晓霞，谢 刚，韩晓明，谢克明

（太原理工大学 信息工程学院，山西 太原 030024）

提出一种基于自适应混沌粒子群优化和支持向量机结合的非线性预测建模算法（ACPSO-SVR），引入ACPSO启发式寻优机制对SVR模型的超参数进行自动选取，在超参数取值范围变化较大的情况下，效果明显优于网格式搜索算法。选取UCI机器学习数据库中的Forest fires标准数据集进行测试，实验结果表明该方法具有较高的精度和良好的泛化能力，对于解决多变量的回归预测问题是一种有效的方法。最后给出了混合算法在碳一多相催化领域的两种典型应用，在反应动力学模型未知的情况下建立催化剂组份模型和操作条件模型，以及基于混合算法的最优催化剂设计框架。

支持向量机；自适应混沌粒子群优化；建模；预测；碳一多相催化剂

许多实际工业过程或研究对象都具有很高的复杂性，其机理尚不十分清楚，或机理方程非常复杂，难以用现有的数学理论建立机理模型。随着人工智能和计算机技术的发展，非线性工业过程建模技术和方法主要集中在专家经验方法、神经网络方法、模糊逻辑方法、支持向量机方法、模式识别方法、遗传编码方法等方面。

支持向量机（Support Vector Machines，SVM）遵循统计学习VC维理论和结构风险最小化原理 （Structural Risk Minimization，SRM），最早应用于模式识别领域，后来通过引入ε不敏感损失函数概念，推广到ε-SVR （Support Vector Regression，SVR），广泛应用于函数回归问题，成为经验建模中重要的智能建模方法之一。由于SVR能较好地解决小样本、高维、非线性和局部极小点等实际问题，并且可以有效地克服维数灾难和过拟合等问题，己经成功地应用于复杂工业过程的动态建模、系统辨识和控制、数据分析、故障诊断等方面。

针对SVR模型的超参数选择直接影响着SVR的一般性能和回归检验，是确保SVR模型优秀性能的关键，笔者提出自适应混沌粒子群优化算法对SVR模型的超参数进行优化选择，在此基础上，提出了基于ACPSO-SVR的预测模型，并给出了详细的建模与算法流程。应用该方法对UCI数据库的Forest fires回归预测数据进行测试，结果显示基于ACPSO-SVR的预测模型具有较高的精度和良好的泛化能力，对于解决多变量的建模和预测问题是一种有效的方法。最后，给出了该方法在碳一多相催化剂建模与最优化设计中的2种应用。

1 算法理论

1.1 支持向量回归机

支持向量机[1]是统计学习理论中最年轻、最实用的部分，是基于结构风险最小化原理和VC维理论的新型机器学习方法。它最初主要用来解决模式识别问题。1997年，Vapnik等拓宽了SVM的应用范围，成功地解决了小样本、非线性及高维数据的函数回归拟合问题。对于非线性回归，通过引入核函数来简化非线性逼近，将低维空间映射到高维的重建核Hilbert空间，即x→Q（x），然后在高维特征空间中进行线性回归，从而取得在原空间非线性回归的效果。根据Mercer定理[2]计算核函数中的内积运算就可以实现非线性函数拟合。

SVR学习与预测的示意图如图1所示。

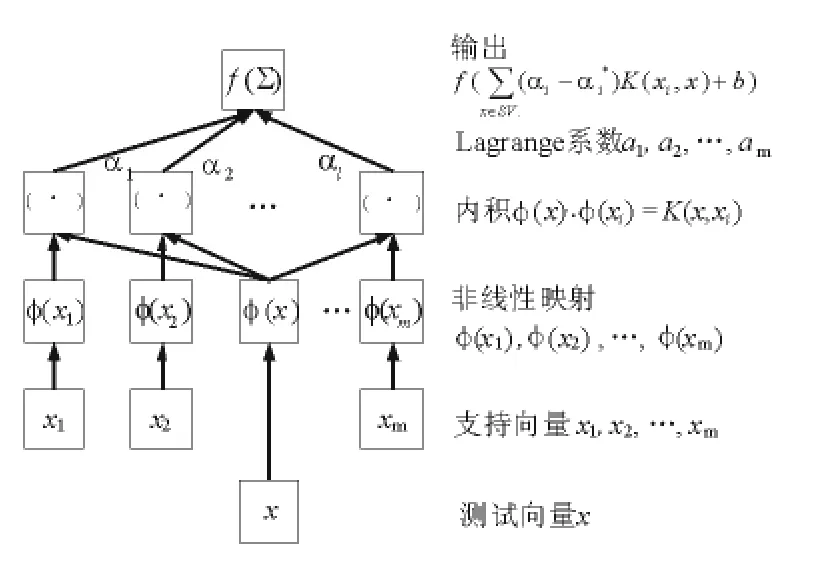
图1 SVR学习与预测算法示意图Fig.1 Schematic diagram of the SVR training and predicting algorithm

图1可见，SVR的训练过程与ANN有着某种类似，两者都具有网络结构和节点权值，但与ANN训练过程中网络结构固定不变不同，在SVR的训练过程中，其网络的结构和权值随着寻优过程的变化而时刻调整着，即在算法的复杂性与预测精度之间进行协调。

对于非线性支持向量机回归，构造SVM回归估计函数：

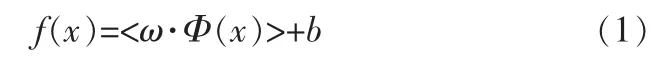
使得预测的期望风险函数最小：

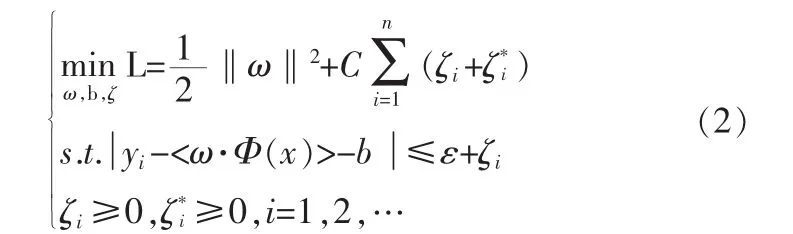
式（2）中，松弛变量（ζi，ζ*i）和惩罚因子 C（>0）用于调节超出ε管道的样本点。惩罚因子C和管道因子ε是两个可以调节的自由参数，C表示模型的复杂性和逼近误差之间的平衡，ε表示训练数据合适的管道宽度[3]。在SVM回归算法求解实际问题只需对支持向量进行，支持向量可以看做是压缩了的训练集里信息量最真实的数据点，于是最终的回归估计函数形式为：

其中K为核函数，采用不同的核函数可以构建出不同的支持向量回归机。 文中采用径向基核（Gaussian 核），K（x，xi）=exp[-（x-xi）/2σ2]，它对于常见的模式识别问题都具有优异的泛化性能。以上自由参数和核函数的选择共同决定SVR回归估计的准确性和泛化能力。

1.2 自适应混沌粒子群算法

自适应混沌粒子群优化 （Adaptive Chaos Particle Swarm Optimization，ACPSO）算法引入混沌优化思想和自适应惯性权调整策略，利用混沌特性提高种群的多样性和粒子搜索的遍历性，将混沌状态引入到优化变量使粒子获得持续搜索的能力；引入自适应惯性权系数 （Adaptive Inertia Weight Factor，AIWF）[4]，提高算法效率，避免陷入早熟，有利于全局范围内产生很好的搜索能力。

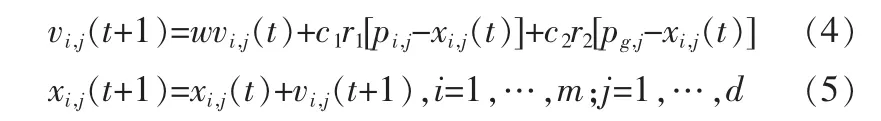
已知基本粒子群优化算法[5]按公式（4）和（5）分别更新各粒子的速度和位置：在ACPSO算法中，采用自适应惯性权系数AIWF来动态调节惯性权重w，其计算公式如下：

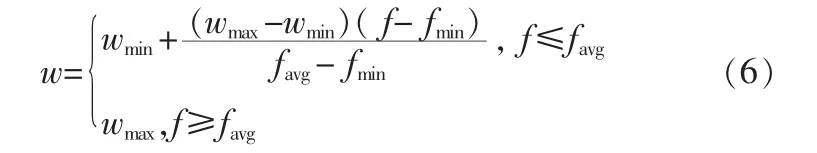
其中，wmax和 wmin分别代表惯性权重w的最大值和最小值，f为粒子当前的目标函数值，favg和 fmin分别为所有粒子的平均值和最小目标值。

当各粒子的目标值区域一致或者趋于局部最优时，将使w增加；而当各粒子的目标值比较分散时，将使w减少。同时，对于目标值f优于平均目标值favg的粒子，将对应于较小的w，从而使该粒子得以保护；而对于目标值f差于平均目标值favg的粒子，将对应于较高的w，从而使该粒子能够更快地趋向较好的搜索空间。

ACPSO算法是一个两阶段算法，其中AIFW调整算法主要用于执行全局搜索，而混沌优化搜索[6-7]除了在初始阶段产生混沌序列之外，将根据PSO算法的结果执行局部搜索。

1.3 建模与算法流程图

将ACPSO-SVR混合算法应用于非线性系统建模与预测中，建模流程如图2所示。本文选用libSVM工具箱ε-SVR回归，SVR 超参数（C，σ，ε）采用 ACPSO 算法优化，核函数选用RBF核函数，目标函数采用CV意义下的性能指标对网格上的每组参数对（C，σ，ε）进行泛化能力评价，libSVM工具箱中ε-SVR回归的性能指标采用均方误差MSE（Mean Squared Error）、根均方误差 RMSE（Root Mean Squared Error）和相关系数 CC（Squared Correlation Coefficient）。

2 算法性能分析

图2 ACPSO算法优化SVR超参数流程图Fig.2 Modeling flow diagram based on ACPSO-SVR

为验证本文提出的ACPSO-SVR建模方法的预测能力，选取UCI机器学习数据库（http://archive.ics.uci.edu/ml/）中的Forest Fires标准数据集进行测试。Forest Fires数据集是一个预测森林火灾发生地的数据库，数据集规模517×13，属于多变量的预测问题。实验的硬件环境为PIV3.4 GHz，1 G内存，120 G硬盘；仿真工具为Matlab7.0。

首先将原始数据预处理，归一化到[0，1]之间。选用ε-SVR回归算法，高斯基RBF核函数，10-fold交叉验证模式。设置SVR模型参数的取值范围：惩罚参数c的变化范围（取以2为底的对数后）为[2-10，210]，RBF函数宽度σ的变化范围（取以 2 为底的对数后）为[2-5，25]，损失函数 ε =0.001，SVR 模型输出为均方误差MSE和相关系数R。设置ACPSO的参数取值范围：学习因子c1=1.5，c2=1.7，最大迭代次数 M=200，种群规模PoP=20。

图3所示为采用ACPSO对SVR模型参数选择结果图。

图3 基于ACPSO的SVR模型参数优化结果图Fig.3 Optimization results of SVR model based on ACPSO

其中（a）图是SVR参数初选结果，（b）图为将参数c和σ的取值范围依据 （a）图结果进一步缩小范围后的精选结果图。粗选结果：Best Cross Validation MSE=0.000 961 388，Best c=0.29，Best g=2，由图 3（a），对应 MSE 最小处，重新设置惩罚参数c的变化范围 （取以2为底的对数后）为[20，210]，RBF函数宽度σ的变化范围（取以2为底的对数后）为[2-2，23]，得到最好的 Best c=0.17，Best g=2.5，回归结果：均方误差 MSE=1.950 29e-005，相关系数R=99.934 5%。

图4（a）所示为SVR参数精选过程中ACPSO的适应度曲线，（b）所示为ACPSO-SVR回归预测的误差曲线，结果表明基于ACPSO-SVR的预测算法具有良好的回归能力，对于多变量回归问题能保证良好的预测精度。

3 算法应用

随着国民经济的发展，尤其新能源需求、新材料的不断涌现，多相催化科学与技术面临新的挑战，既要从经济、安全、多功能等方面寻求新型、高效的催化剂，又要从化学进程全局出发全面考察催化剂的性能。作为催化领域的难点和迫切需要解决的3个关键问题：催化剂的动力学关系模型、催化剂的活性关系模型、催化剂的优化设计，这无论是对于催化剂对象的特性研究，还是实际化工生产过程控制、优化、模拟等都具有重要的现实意义。作者尝试在碳一催化剂的建模与最优化设计中，使用本文提出的非线性系统建模与预测算法，克服传统催化剂研发中反复 “试错”试验的缺陷，缩短了催化剂研发的时间，节约资金和降低时间的消耗，取得了一定的成果。

3.1 建模与预测中应用

煤基二甲醚（简称DME），在我国富煤、贫油、少气的能源环境下，成为优先发展的替代能源。而影响浆态床二甲醚合成工业化进程的关键因素是催化剂稳定性和活性之间的关系。将本文提出的ACPSO-SVR建模与预测方法应用于合成二甲醚多相催化剂实验室制备中，结合两种催化剂各自优点，寻求一种Cu-Zn-Al-Zr的新配方组分，以及最佳的制备条件，提高CO转化率和二甲醚的选择性。

图4 基于ACPSO-SVR预测算法性能曲线Fig.4 Performance curves of ACPSO-SVR prediction algorithm

图5所示为基于ACPSO-SVR建模与预测示意图。以催化剂的组分（Cu-Zn-Al-Zr）和制备条件（温度、搅拌回流时间、加料方式）作为输入变量。催化剂性能指标（CO转化率、二甲醚的选择性）作为输出变量，建立Cu-Zn-Al-Zr浆状催化剂动态模型，实现预测。

图5 基于多相催化历史数据的SVR建模示意图Fig.5 Configuration of SVR model based heterogeneous catalysis historical data

3.2 最优化设计中应用

多相催化过程是个混合过程，过程的优化目标属于多目标优化，可以描述为：给定过程的操作变量值或多相催化剂的组分变量值作为输入变量，以及相应的过程输出变量值，如催化剂的活性和选择性、目标产物的转化率等，寻求输入变量的最优值，使得预先指定的过程性能同时最大，即发现具有最佳组分或最佳操作条件下的具有最优催化性能的最优催化剂。

然而，在多相催化领域，获取催化剂性能评价（活性、选择性、稳定性）非常困难，需要反复的制备、表征，不借助软计算方法来发现最优组分和最优制备条件下的催化剂，其成本和时间耗费难以想象。将训练好的ACPSO-SVR模型作为最优化设计方法中的适应度评价模型，试图通过ACPSO-SVR最优化设计来解决上述多相催化剂实验室设计问题。

4 结 论

本文提出了一种非线性系统的建模与预测的新方法，该算法理论上具有全局最优点，解决了神经网络方法无法避免的局部最优解和网络结构难以选择等问题，同时克服了维数灾难问题，SVR算法的复杂度与样本维数无关，具有良好的泛化能力。

仿真结果表明，将ACPSO算法的智能搜索用于ε-SVR支持向量回归机算法的参数选择过程中，与K-CV（K-fold cross validation）意义下的穷尽式网格搜索算法（Grid-search Method）相比，能够在更大的参数空间内，不必遍历网格内的所有参数点，以较少的搜索次数获得全局最优解，使得SVR算法具有良好的泛化能力和逼近精度。

[1]VAPNIK V.The nature of statistical learning theory[M].New York:Springer，1995.

[2]Burges C J C.A tutorial on support vector machines for pattern recognition[J].Data Mining and Knowledge Discovery，1998（2）:121-167.

[3]Cherkassky V，Yunqian M.Practical selection of SVM parameters and noise estimation for SVM regression[J].Neural Networks，2004（17）:113-126.

[4]王凌，刘波.微粒群优化与调度算法[M].北京：清华大学出版社，2008.

[5]Kennedy J，Eberhart R C.Particle swarm optimization[C]//Proc IEEE International Conference on Neural Networks，Perth， Australiam， Piscataway:IEEE Press，1995:1942-1948.

[6]李兵，蒋慰孙.混沌优化方法及其应用[J].控制理论与应用，1997，14 （4）:613-615.

LI Bing，JIANG Wei-sun.Chaos optimization method and its application[J].Control Theory&Applications，1997，14（4）:613-615.

[7]贾东立，张家树.基于混沌变异的小生境粒子群算法[J].控制与决策，2007，22（1）:117-120.

JIA Dong-li，ZHANG Jia-shu.Niche particle swarm optimization combined with chaotic mutation[J].Control and Decision，2007，22（1）:117-120.

Application of adaptive chaos particle swarm optimization and support vector regression for modeling and forecasting of nonlinear system

HAN Xiao-xia， XIE Gang， HAN Xiao-ming， XIE Ke-ming
（College of Information Engineering，Taiyuan University of Technology，Taiyuan030024，China）

An effective relevance prediction algorithm is presented for nonlinear system forecasting and modeling based on adaptive chaos particle swarm optimization and support vector regression，namely ACPSO-SVR method.A heuristic optimization method ACPSO was introduced to automatic selection of hyper-parameters in SVR.The forest fires standard data set of UCI machine learning database was selected to test.The experimental results showed that the new method has high relatively precision and good generalization ability with a wide range of parameter values，better than that of mesh searching algorithm.It could be used as an effective method to solve the problems of multivariate regression predication.Moreover，two main applications were introduced in C1 heterogeneous catalysts yield，obtaining the catalyst composition model and the kinetic model，and building the optimization framework of catalyst development in laboratory.

support vector regression； adaptive chaos particle swarm optimization； modeling； forecasting； C1 heterogeneous catalysts

TP391

A

1674－6236（2012）05-0014-04

2012-01-06稿件编号：201201017

国家自然科学基金（60975032）；国家青年科学基金资助（20606022）

韩晓霞（1976—），女，山西忻州神池人，博士，讲师。研究方向：智能控制理论与应用，软计算方法，智能传感器与检测技术。