基于充氩夫兰克-赫兹实验的非弹性碰撞模型
2012-09-26杨春沪张素才
杨春沪,张素才
(上海电力学院数理学院 ,上海 200090)
基于慢电子和稀薄气体中的原子发生碰撞的夫兰克-赫兹实验揭示了原子内部能量的量子化效应,为波尔理论提供了直接有力的实验依据.1925年,科学家夫兰克与赫兹基于此项工作获得了诺贝尔物理学奖.该实验的内容是对原子的第一激发能级的测定,由于其涉及的过程比较复杂,使得定量研究存在一定的困难.文献[1]至文献[4]对定量测量的结果进行了分析、讨论和修正,使其更符合理论值.本文提出了一种新的模型来阐述电子与原子间非弹性碰撞的过程,并用该模型来确定原子的第一激发能级.
1 实验基本原理
夫兰克-赫兹实验的原理[1,5]如图 1 所示.在夫兰克-赫兹管中,电子通过第一栅极 G1进入G1G2区域,与管中的氩原子发生碰撞.当加速电压UG2k较小时,电子和原子的碰撞为弹性碰撞,损失的能量很小.当加速电压超过原子的第一激发电位时,电子和原子发生非弹性碰撞,碰撞后电子将动能部分或全部传递给被测原子,使其跃迁到第一激发态,而电子本身所剩能量很小,不能克服拒斥电压到达板极A,导致板极电流显著下降.由于原子内部能量是量子化的,因此板极的电流会随着加速电压的增加而发生规律性的起伏变化,如图2所示.
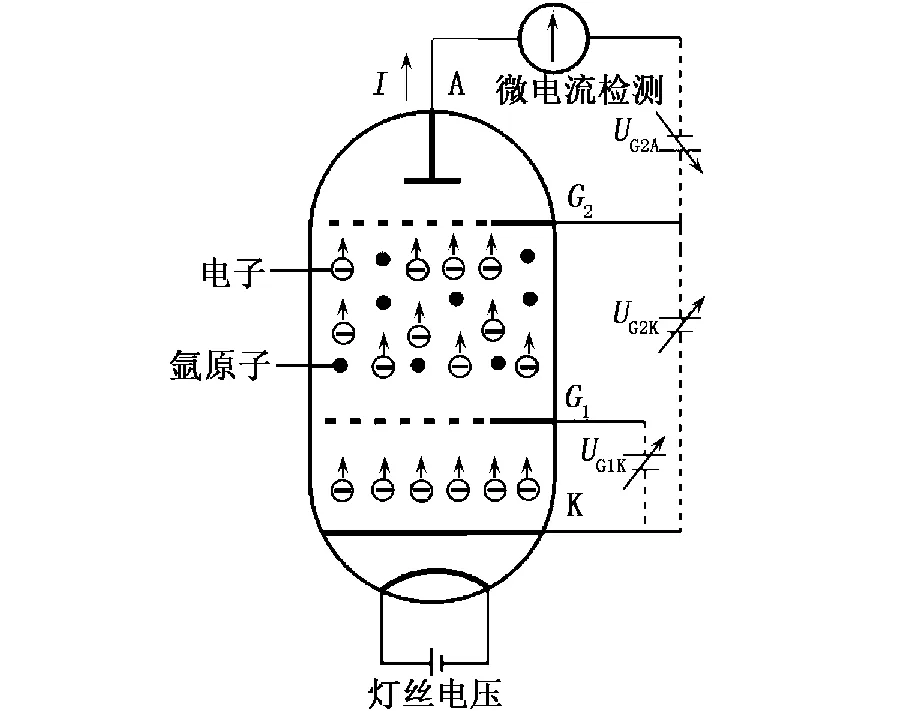
图1 夫兰克-赫兹原理
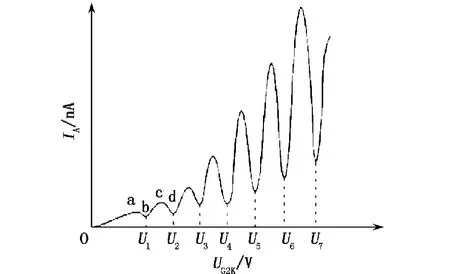
图2 板极电流的变化曲线
2 非弹性碰撞模型
在充氩夫兰克-赫兹管中,在加速电压UG2k的作用下,电子在G1G2区域内与氩原子发生碰撞的运动过程如图3所示.当电子的能量小于氩原子从基态跃迁到第一激发态所需的能量(即临界能量)时,电子和氩原子之间只发生弹性碰撞,由于两者的质量差距很大,因此电子损失的能量非常小;当电子的能量达到氩原子的临界能量时,电子和氩原子可能发生非弹性碰撞.当然在发生非弹性碰撞之前,电子所具有的能量和氩原子的第一激发能量必须非常接近.
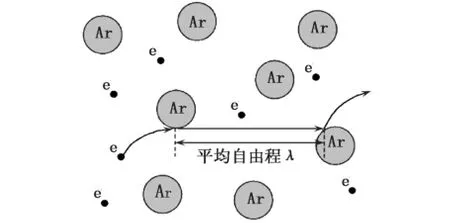
图3 电子与原子碰撞原理
在非弹性碰撞前,电子所走过的平均距离称为平均自由程.如果电子在平均自由程的距离内没有与氩原子发生非弹性碰撞,则它在运动途中将继续获得能量,这就有可能使氩原子不仅被激发到第一激发态,而且可能被激发到更高的能级上去.这种情况会影响夫兰克-赫兹实验曲线,因此在分析实验数据时必须被考虑进去.
图4为一个自由电子在夫兰克-赫兹管从第一栅极G1到第二栅极G2区域内获得能量的过程.
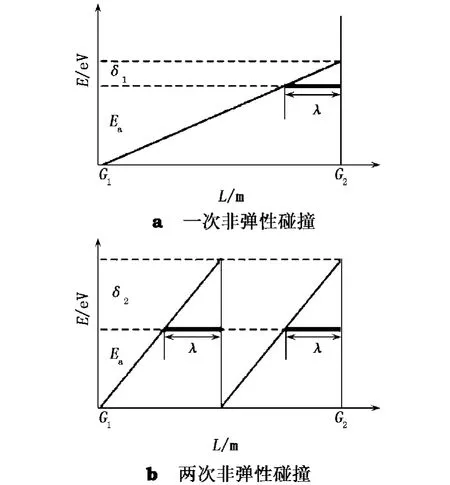
图4 夫兰克-赫兹管从G1到G2区域内电子能量变化过程
图4a中,电子在加速电压UG2k的作用下,获得了氩原子第一激发能级Ea的能量后,又经过了λ的距离才到达第二栅极G2,在这段距离中,电子又额外获得了能量δ1,这增大了电子和氩原子的非弹性碰撞几率.在原子的第一激发能级Ea之上,有很多其他的能级存在并可能被激发,由此可以假设一个电子在发生非弹性碰撞后,失去了绝大部分的能量.图4b中的加速电压UG2k比图4a中的大,电子和氩原子发生了两次非弹性碰撞.电子在平均自由程λ的距离上获得的能量δ2大于δ1,在G1G2区域内获得的总能量为 E2=2Ea+2δ2.这种情况对应于夫兰克-赫兹实验曲线中的第2个谷值的位置.电子在发生第n次非弹性碰撞过程中,获得的总能量为:
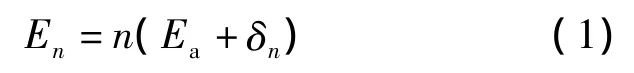
在典型管压下,电子的平均自由程λ远小于两个栅极G1G2之间的距离L,即λ<<L,那么 δn<< Ea,则有:

由式(1)和式(2)可以得到夫兰克-赫兹实验曲线中谷值之间的间距为:

由式(3)可以看出,随着n的增大,谷值之间的间距也随之增大,这与实验结果相一致.由式(3)还可以得到原子的第一激发能级:

由式(4)可知,第一激发能级的值为n=0.5时谷值间隔ΔE的大小.根据这个推论结果,在夫兰克-赫兹实验曲线图上无法直接计算得到第一激发能级的大小.在实验过程中,我们可以作出ΔE-n的关系图,在图中可以求出n=0.5时对应ΔE的值,即为Ea的大小.
3 实验结果与分析
本实验采用DH4507型夫兰克-赫兹实验仪,被测气体为氩气.最佳工作参量值为:灯丝电压UF=3.3 V,第一栅极电压 UG1k=2.2 V,拒斥电压UG2A=6.0 V.将仪器设定为自动扫描状态,记录下加速电压UG2k与板极电流IA的关系曲线图(扫描步进为0.2 V).根据UG2k-IA曲线图,可以得到图中6个谷值所对应的加速电压值,见表1.
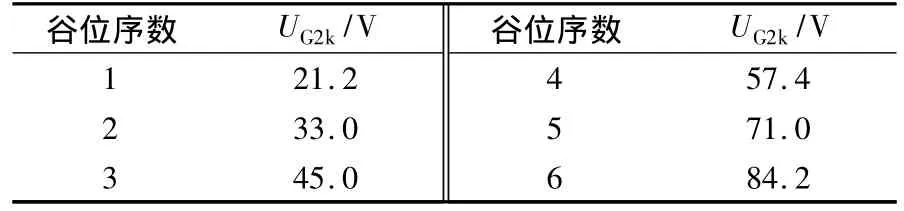
表1 谷位序数与对应的加速电压实验结果
根据表1中的实验数据,利用非弹性碰撞模型可以作出夫兰克-赫兹实验曲线中对应的谷值间隔ΔE与谷值个数 n的关系图,见图5.根据ΔE-n的数据点,给出线性拟合直线,这符合非弹性碰撞理论模型中的式(3).根据式(4)可以计算出氩原子的第一激发能级Ea=11.31 eV(即n=0.5时,ΔE 的值);第一激发电位 Ua=11.31 V,与公认值11.5 V比较,相对不确定度为1.7%.
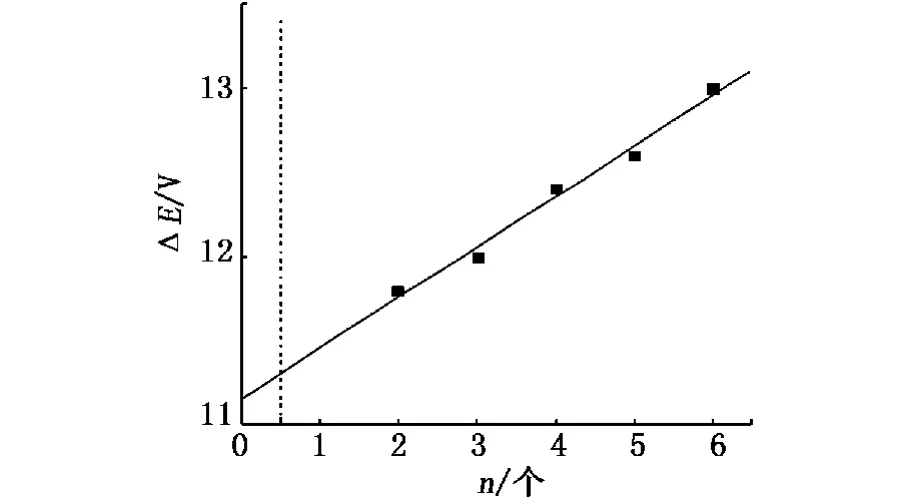
图5 谷值间隔ΔE与谷值个数n的关系
4 结语
本文对充氩夫兰克-赫兹实验IA-UG2K曲线中谷值间距随着谷值个数而线性增加的实验现象进行了研究,给出了非弹性碰撞模型,并得出了求得氩原子第一激发能级的新方法.应用这一模型对实验数据进行处理,最后求出的氩原子第一激发电位与公认值非常接近,不确定度为0.2 V.
[1]朱筱玮,陈永丽.充氩弗兰克-赫兹实验研究[J].大学物理,2007,26(7):46-48.
[2]王梅生.弗兰克-赫兹实验中的峰间距问题[J].物理实验,2001,21(11):40-43.
[3]陈发堂.充氖夫兰克-赫兹实验数据误差的修正[J].上海电力学院学报,2006,22(2):181-183.
[4]胡芳林,唐泉清.Ar原子最外层8个电子的能级[J].物理实验,2009,22(1):41-46.
[5]褚圣麟.原子物理学[M].北京:人民教育出版社,1976:45-47.
