谷值V2控制Boost变换器的频域与时域特性分析
2015-05-25何圣仲周国华许建平吴松荣徐英雷
何圣仲, 周国华, 许建平, 吴松荣, 徐英雷, 陈 利
(西南交通大学电气工程学院,四川成都 610031)
随着电力电子技术的发展以及新能源的开发 和利用,电子设备对开关电源的响应速度、稳定性和稳压精度均提出了较高的要求.例如,当负载快速、频繁变化时,开关电源的输出电压亦会随着负载变化而波动,从而影响电子设备的工作性能,严重时甚至导致电子设备无法正常工作[1].因此要求开关电源具有快速的负载动态响应速度,以满足其负载变化的要求[2,3].V2控制技术是在电流型控制技术的基础上发展起来的,它自1996年被提出以来,因其快速的负载动态响应受到极大的关注[4].目前,对V2控制开关DC-DC变换器的研究主要集中于V2控制Buck变换器小信号建模分析及控制器设计等[5-7].随着开关变换器数字控制技术的发展,V2控制的数字控制技术也受到了研究者们的大量关注[8-9].模拟或数字实现的 V2控制的研究结果均表明,V2控制本质上是基于输出电压纹波的控制方法,具有优异的瞬态性能.然而,当V2控制开关变换器的输出电容等效串联电阻(equivalent series resistance,ESR)较小时,V2控制会出现次谐波振荡,甚至失控[10].文献[11-12]提出在V2控制的内环增加微分和积分环节来获得电感电流纹波信息,使V2控制开关DC-DC变换器在ESR较小时能够稳定运行.现有文献对V2控制开关变换器的研究主要集中于峰值V2控制Buck变换器,谷值V2控制的概念于2011年在文献[11]中首次被提出,该文献分析了谷值V2控制Buck变换器的工作原理与瞬态特性,并指出谷值V2控制Buck变换器具有比谷值电流控制Buck变换器更快的负载动态响应速度.对于V2控制Boost变换器的研究,则鲜有文献报道.基于传统的V2控制技术(指峰值V2控制),文献[14]给出了V2控制方法不能应用于Boost变换器的结论.

图1 谷值V2控制Boost变换器Fig.1 Valley V2controlled Boost converter
本文在详细分析V2控制Boost变换器工作原理的基础上,采用开关网络平均法建立了其小信号模型,基于小信号模型,推导了控制-输出、输入-输出、输入-电感电流、控制-电感电流和输出阻抗等传递函数,研究了V2控制Boost变换器的频域和时域特性,并与谷值电流控制Boost变换器进行了比较,最后进行了仿真和实验验证.
1 谷值V2控制Boost变换器工作原理
为了更好地讨论谷值V2控制Boost变换器的工作原理,又不失工程应用的一般性,作如下假设:
(1)Boost变换器的开关频率远远大于Boost变换器的固有频率;在开关频率处,输出电容支路的阻抗远小于负载阻抗;
(2)开关管S导通时,电感电流线性上升;开关管S关断时,电感电流线性下降.
图1(a)所示为谷值V2控制Boost变换器示意图,其中控制器主要由误差放大器、比较器和锁存器构成,R1、R2构成内环电压采样电路,Vref为参考电压,CP为时钟信号.谷值V2控制Boost变换器的主要工作波形如图1(b)所示,其中Ts为开关周期.
在每个开关周期初始时刻,时钟脉冲信号使锁存器复位,通过驱动电路控制开关管S关断,二极管D导通,电感电压vL=vg-vo<0,电感电流线性下降,且满足iL(t)=ILmax+((vg-vo)/L)t.此时,输出电压满足vo(t)=Vcap+(iL(t)-Io)re.开关管S关断期间,由于输出电容较大,开关频率很高,输出电容电压Vcap可认为保持不变,输出电压变化与电感电流变化近似满足Δv=reΔiL.开关管S关断期间,电感电流线性下降,使得输出电压也近似线性下降,下降斜率为-m2=((vg-vo)/L)re.内环检测电压vs=Kvvo,其中Kv=R2/(R1+R2)为内环反馈电压采样比例系数.当vs下降到谷值控制电压vk时,比较器翻转,使锁存器置位,开关管S导通,电感电压vL=vg>0,电感电流线性上升且满足iL(t)=ILmin+vg(t-Toff)/L.此时,二极管D 关断,输出电容为负载供电,输出电压满足vo(t)=(R/(R+re))Vcap.输出电容电压因为电容放电而略微减小,相应地vs也有所下降;如果忽略Vcap的变化,输出电压也保持不变,直到下一个开关周期到来.
2 小信号建模
为了分析谷值V2控制Boost变换器的频域特性,必须建立其小信号模型.本节先分别建立包含ESR的Boost变换器主电路和谷值V2控制环节的小信号模型,然后将二者结合起来构成谷值V2控制Boost变换器的小信号模型.
2.1 Boost变换器的小信号模型
工作于连续导电模式(continuous conduction mode,CCM)的Boost变换器的小信号建模方法很多,如状态空间平均法[15]、时间平均法[16]、开关元件平均模型法、开关网络平均模型法[17]等.本文采用开关网络平均法建立含有输出电容ESR的Boost变换器小信号模型,如图2所示,其中D'=1-Dload为负载扰动.

图2 含ESR的Boost变换器的小信号模型Fig.2 Small-signal model of valley V2controlled Boost converter with ESR
基于图2所示电路,可得到含输出电容ESR的Boost变换器的传递函数.





2.2 谷值V2控制Boost变换器的小信号模型
由谷值V2控制Boost变换器工作原理可知,开关管S由关断到导通切换时,满足
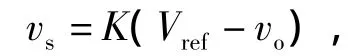
由于采样电压vs=Kvvo,所以有

式中:K为误差放大器的比例系数.
由式(7),结合谷值V2控制Boost变换器的工作原理,图3给出了CCM模式时谷值V2控制环节的关键波形,其中v'k为开关管S由关断状态切换为导通状态时的阀值电压,va为开关管S导通时的输出电压值,¯vo为输出电压平均值.

图3 CCM模式时谷值V2控制环节的关键波形Fig.3 Typical wave of valley V2control in CCM
由图3可得

当电容C足够大时,Vcap≈,则式(8)可写为


将式(10)代入式(9),将变量的直流信号和小信号扰动分离,并忽略高阶扰动量,可得到小信号特征表达式:

对式(9)中的相关变量取小信号扰动:
结合式(6)和式(11),可得到CCM模式谷值V2控制Boost变换器的闭环小信号框图,如图4所示.
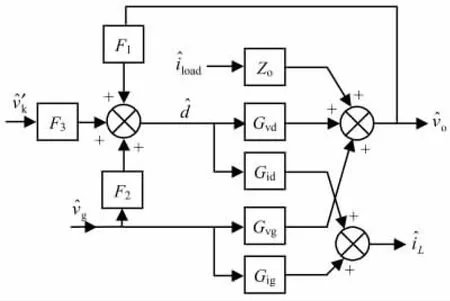
图4 谷值V2控制Boost变换器的小信号框图Fig.4 Small-signal diagram of valley V2controlled Boost converter
基于图4,结合式(1)~(6)和式(11)可得谷值V2控制Boost变换器闭环交流小信号传递函数.



2.3 谷值电流控制Boost变换器的小信号模型
为了比较谷值V2与谷值电流控制Boost变换器的频域特性,需要获得谷值电流控制Boost变换器的小信号模型.采用文献[18-19]中的方法,可推出谷值电流控制Boost变换器的占空比交流小信号表达式:

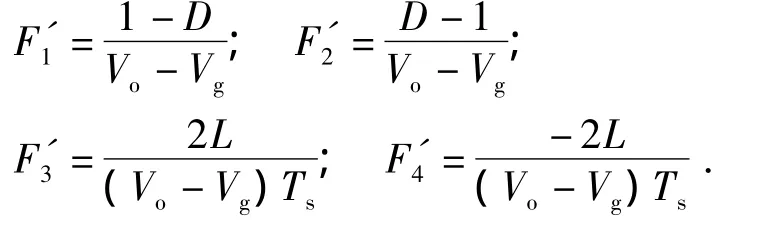
结合式(1)~(6)和式(15),可得谷值电流控制Boost变换器闭环输入-输出传递函数G″vg(s)、闭环控制-输出传递函数 G″vc(s)和闭环输出阻抗Z″
out(s)分别为

3 频域和时域特性分析
3.1 频域特性分析
选择表1所示的电路参数,利用Matlab软件建立仿真模型,对谷值V2和谷值电流控制Boost变换器进行频域特性分析.

表1 谷值V2和谷值电流控制Boost变换器电路参数Tab.1 Circuit parameters of valley V2and VCM controlled Boost converter
(1)控制-输出特性
控制-输出传递函数体现的是内环反馈的控制作用.内环反馈的引入会降低控制-输出传递函数的增益,从而对功率级传递函数产生影响,增益降低得越多说明内控制环控制作用越明显.
图5给出了采用谷值V2控制和谷值电流控制的控制-输出传递函数的波特图.

图5 控制-输出传递函数的波特图Fig.5 Bode diagram of control-to-output transfer function
从图5可以看出,与谷值电流控制相比,谷值V2控制具有更小的低频增益,表明谷值V2控制的内环控制作用更强;另一方面,谷值V2控制的穿越频率比谷值电流控制穿越频率更高(亦即带宽更宽),表明谷值V2控制的瞬态调节时间更短、响应速度更快.
(2)输出阻抗特性
图6给出了采用谷值V2控制和电流型控制的输出阻抗波特图.输出阻抗体现的是负载变化时的响应速度.由图6可以看出,在整个低频率范围内,谷值V2控制具有比谷值电流控制更低的输出阻抗,表明谷值V2控制具有更快的负载动态响应速度.

图6 输出阻抗的波特图Fig.6 Bode diagram of output impedance
(3)输入-输出特性
输入-输出传递函数体现的是输入电压变化对输出的影响.图7给出了采用谷值V2控制和电流型控制的输入-输出传递函数的波特图.
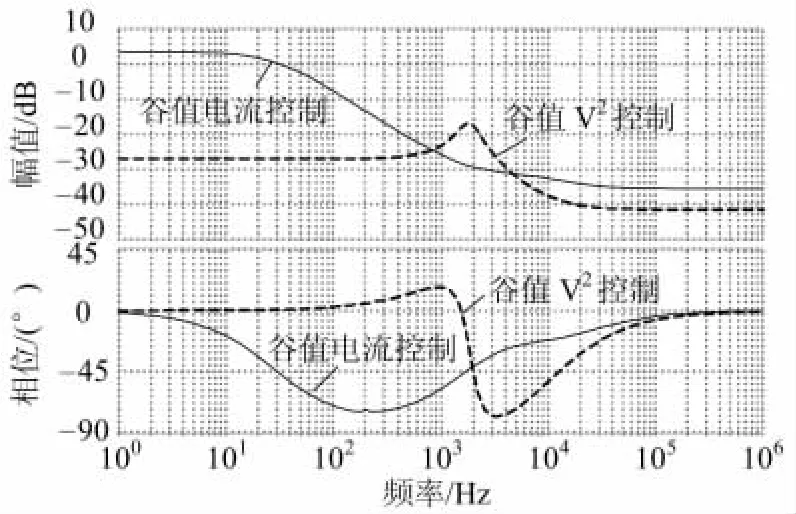
图7 输入-输出传递函数的波特图Fig.7 Bode diagram of input-to-output transfer functions
从图7可以看出,与谷值电流控制相比,谷值V2控制的低频增益更小,表明谷值V2控制对输入电压扰动具有更好的抑制能力.
3.2 时域特性分析
采用与频域特性分析相同的参数,利用Psim仿真软件对谷值V2控制和谷值电流控制Boost变换器进行时域仿真.为了比较两种控制方法下Boost变换器的输入、负载瞬态响应,令输入电压突变为 vg从3.5 V 突增至4.5 V,或者从4.5 V 突减至3.5 V;令输出负载突变为负载电流从0.5 A突增至1.0 A或者从1.0 A 突减至0.5 A.
(1)输入瞬态响应
在t=100 ms时,输入电压vg从3.5 V突增至4.5 V时,谷值V2控制和谷值电流控制Boost变换器的输出电压瞬态响应波形如图8所示.从图8(a)可以看出,当输入电压从3.5 V突变至4.5 V时,谷值V2控制Boost变换器的输出电压超调量Δv约为 15 mV,调整时间 Δt约为 470 μs;从图8(b)可以看出,当输入电压从3.5 V 突 变 至4.5 V时,谷值电流控制Boost变换器的 Δv约为16 mV,Δt比谷值 V2控制的长,约为 1 000 μs.

图8 输入电压vg突增时的瞬态响应波形Fig.8 Transient responses when vgincreases
在 t=100 ms时,vg从 4.5 V 突减至3.5 V,谷值V2控制和谷值电流控制Boost变换器的输出电压瞬态响应波形如图9所示.从图9(a)可以看出,当输入电压从4.5 V突减至3.5 V时,谷值V2控制Boost变换器的输出电压跌落量Δv很小,约为70 mV,Δt约为 400 μs;从图 9(b)可以看出,当输入电压从4.5 V突减至3.5 V时,谷值电流控制Boost变换器的Δv也很小,约为75 mV,Δt比V2控制的要长很多,约为1 200 μs.

图9 输入电压vg突减时的瞬态响应波形Fig.9 Transient responses when vgdecreases
(2)负载瞬态响应
在t=100 ms时,负载电流从0.5 A突增至1.0 A,谷值V2控制和谷值电流控制Boost变换器的输出电压瞬态响应波形如图10所示.
从图10(a)可以看出,当负载电流从0.5 A突增至1.0 A时,谷值V2控制Boost变换器的输出电压跌落量 Δv约为 125 mV,Δt约为 700 μs;从图10(b)可以看出,当负载电流从0.5 A突增至1.0 A时,谷值电流控制Boost变换器的 Δv约为140 mV,Δt约为 1 350 μs.
在t=100 ms时,负载电流从1.0 A突减至0.5 A,谷值V2控制和谷值电流控制Boost变换器的输出电压瞬态响应波形如图11所示.
从图11(a)可以看出,当负载电流从1.0 A突减至0.5 A时,谷值V2控制Boost变换器的输出电压超调量Δv约为45 mV,Δt约为510 μs;从图11(b)可以看出,当负载电流从1.0 A突减至0.5 A时,谷值电流控制Boost变换器的Δv约为52 mV,Δt约为 1 840 μs.

图10 负载突增时的瞬态响应波形Fig.10 Transient responses when the load increases

图11 负载突减时的瞬态响应波形Fig.11 Transient responses when the load decreases
4 实验验证
为了验证谷值V2控制Boost变换器原理与瞬态特性分析的正确性,选择表1中电路参数,搭建相应的实验平台,对谷值V2控制Boost变换器的负载瞬态响应进行了实验验证,实验结果如图12所示.

图12 负载突变时的瞬态响应实验波形Fig.12 Experiment waves of transient responses when load changes
从图12可以看出,谷值V2控制Boost变换器负载增加时的瞬态响应时间约为800 μs,负载突减时的瞬态响应时间约为540 μs,实验结果与仿真结果基本一致,从而验证了理论分析与仿真结果的正确性.
5 结论
本文首次建立了谷值V2控制Boost变换器的小信号模型,推导了相应的传递函数,研究了其频域特性和时域特性,并与谷值电流控制Boost变换器进行了比较.研究结果表明:与谷值电流控制Boost变换器相比,谷值V2控制Boost变换器具有更小的低频增益、更宽的带宽、更低的输出阻抗,因此,谷值V2控制Boost变换器输入和负载瞬态调节时间更短、响应速度更快.搭建了相应的实验平台,用实验结果验证了理论和仿真分析的正确性.参考文献:
[1]LAW Y Y,KONG J H,LIU J C P,et al.Comparison of three topologies for VRM fast transient application[C]∥Applied Power Electronics Conference and Exposition,2002.Dalas:IEEE,2002:210-215.
[2]周国华,陈兴,崔恒丰.双缘COT调制数字电压型控制Buck变换器分析[J].西南交通大学学报,2015,50(1):13-19.
ZHOU Guohua,CHEN Xing,CUI Hengfeng.Analysis of digital voltage-mode controlled Buck converter with dual-edge constant on-time modulation[J].Journal of Southwest Jiaotong University,2015,50(1):13-19.
[3]吴松荣,钟曙,许建平,等.变脉宽脉冲序列控制DCM Buck变换器[J].西南交通大学学报,2014,49(3):455-461.
WU Songrong,ZHONG Shu, XU Jianping, et al.Variablewidth pulse train controlled DCM Buck converter[J].Journal of Southwest Jiaotong University,2014,49(3):455-461.
[4]GODER D,PELLETIER W.V2architecture provides ultra-fast transient response in switch power supplies[C]∥ Proceedings of High Frequency Power Conversion.Las Vegas:[s.n.],1996:19-23.
[5]王凤岩,王金平,许峻峰.V2控制Buck变换器分析[J].中国电机工程学报,2005,25(12):67-72.
WANG Fengyan,WANG Jinping,XU Junfeng.Modeling and analysis of V2controlled buck converter[J].Proceeding of the CSEE,2005,25(12):67-72.
[6]WANG M.Power supply design with fast transient response using V2control scheme[C]∥Proceedings of International IC'99.[S.l.]:EET,1999:189-199.
[7]QU S. Modeling and design considerations of V2controlled buck regulator[C]∥Applied Power Electronics Conference and Exposition, 2001.Anaheim:IEEE,2001:507-513.
[8]周国华,许建平,金艳艳.非对称三角后缘调制数字V2控制Buck变换器分析[J].中国电机工程学报,2009,29(33):15-21.
ZHOU Guohua,XU Jianping,JIN Yanyan.Analysis of digital V2controlled buck converter with asymmetrical trailing-triangle modul ation[J]. Proceedingofthe CSEE,2009,29(33):15-21.
[9]PRODIC A,MAKSIMOVIC D,ERICKSON R.Design and implementation of a digital PWM controller for a high-frequency switching DC DC power converter[C]∥The 27th Annual Conference of the IEEE Industrial Electronics Society.Denver:IEEE,2001:893-898.
[10]REDL R,SUN J.Ripple-based control of switching regulators-an overview[J].IEEE Transactions on Power Electronics,2009,24(12):2669-2680.
[11]LEE Y H,WANG S J,CHEN K H.Quadratic differential and integration techniquein V2control buck converter with small ESR capacitor[J]. Power Electronics,2010,25(4):829-838.
[12]MAI Y Y,MOK P K T A.Constant frequency outputripple-voltage-based buck converter without using large ESR capacitor[J].IEEE Transactions on Circuits and SystemsⅡ,2008,55(8):748-752.
[13]ZHOU Guohua,XU Jianping,SHA Jin,et al.Valley V2control technique for switching converters with fast transient response[C]∥ IEEE ECCE Asia. Jeju:IEEE,2011:2788-2791.
[14]王凤岩.快速瞬态响应电压调节器控制方法的研究[D].西南交通大学,2005.
[15]XU Jianping,LEE C Q.Generalized state space averaging approach for a class of periodically switched networks[J]. IEEE Transactionson Circuitsand SystemsⅠ,1997,44(11):1078-1081.
[16]XU Jianping.Modeling of switching DC-DC converters by time averaging equivalent circuit approach:partⅠ.continuous conduction mode[J].International Journal of Electronics,1993,74(3):465-475.
[17]ERICKSON R W,MAKSIMOVIC D.Fundamentals of power electronics[M]. 2ed. Secaucus:Kluwer Academic Publishers,2001:235-247.
[18]TAN F D,MIDDLEBROOK R D.Unified modeling and measurement of current-programmed converters[C]∥ PowerElectronics Specialists Conference,1993.[S.l.]:IEEE,1993:380-387.
[19]MAKSIMOVIC D,CUK S.A unified analysis of PWM converters in discontinuous modes[J].IEEE Transactions on Power Electronics,1991,6(3):476-490.
