样本数据概率分布的可视化方法

卢亚丽

0 引言

在理论教学中,知道了随机变量的概率密度函数就能获知该随机变量的全部概率分布特性和数字特征,如常见的正态分布、指数分布、均匀分布、二项分布、泊松分布等等。然而,对于在实际学习、工作、以及科学研究中所获得的统计数据序列,我们事先并不知道它们服从什么概率分布。那么这些统计数据序列的概率分布是什么?它们有什么样的统计规律性?如何绘制其概率密度曲线?这常常是人们对统计数据进行分析时所感兴趣的问题[1-2]。由样本数据序列估计其概率分布是统计学及其相关专业的大学生以及经常需要对统计数据进行分析的研究人员所必须掌握的知识。在计算机越来越普及的今天,借助于计算机的快速计算能力,以前估计样本数据概率分布需要花很长时间才能做完的繁琐的计算工作现在可以在计算机上瞬间完成。通过计算机绘图,估计出的样本数据的概率密度函数的图像也可以直接在计算机上显示出来(即计算结果的可视化),从而使我们可以以图像的方式直观的观察样本数据的概率分布规律。这为分析来自理论分布获知困难的样本数据序列的概率分布规律提供了简便、快捷的近似方法。目前,样本数据概率分布的可视化研究,重点在于理解其理论基础、优化其算法设计、清晰化代码编写。本文拟通过理论基础分析,给出样本数据概率分布直方图和概率密度曲线的绘制算法,并用MATLAB 7.0编写程序代码实施计算结果的可视化。

1 方法与程序

1.1 理论基础

样本数据概率分布的估计以大数定律为基础,用频率的稳定值来度量概率。由概率论中贝努力概型知识可知,将一成功(事件A发生)概率为 p的实验独立重复n次,其中成功μn次,则μn为服从二项分布的随机变量,其数学期望和方差分别为:E(μn)=np,D(μn)=np(1-p)。因此,成功的频率μnn也是随机变量,其数学期望和方差分别为:E(μnn)=p。这表明随机变量 μnn的期望为 p,与n无关,且其方差在n→∞时趋于0.由概率论知识知,方差为0的随机变量恒等于它的数学期望.因此,在n→∞时频率μnn应以概率p为极限[3]。从而,“频率以概率为其稳定值”的严格数学刻画可由下面的定理1表示。

定理1设μn为n重贝努力实验中成功的次数,则当与f(x)⋅d x=1 。 记 ξ(k=1,2,…,n)落 入 区 间k[xi-1, xi)的频数为 μi,频率为 μin。从而,由定理1可知,随机点ξk落入区间[xi-1, xi)的概率 pi(即图1中曲边梯形ABCE的面积)可表示为。由积

设独立同分布随机变量ξk(k=1,2,…,n)的概率密度函数为 f(x),其示意图见图1。显然,f(x)满足:f(x)＞0分计算的微元法,也即在区间[xi-1, xi)的宽度很小时,图1中曲边梯形ABCE的面积可以用矩形ABCD的面积近似表示。从而,由定积分计算的右矩形公式可知,概率密度函数 f(x)在 xi点处的函数值可近似表示为

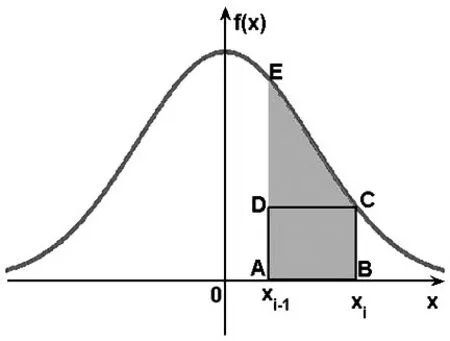
图1 概率密度函数 f(x)曲线

1.2 计算步骤

设{yk},k=1,2,…,m为来自某一实际问题或理论问题的容量为m的样本数据序列,其概率密度的估计可按照以下步骤进行:

① 记 a=min{yk}-ε,b=max{yk}+ε,这里 ε为一很小的正数。

②记a=x0,b=xn,在 x0和 xn之间等距插入n-1个点 xi,i=1,2,…,n-1,把区间[a,b]分割为n个长度相同的小区间[xi-1, xi),i=1,2,…,n。

③统计样本点{yk},k=1,2,…,m落入区间[xi-1, xi)内的个数,记为mi,i=1,2,…,n。从而,样本点落入区间[xi-1, xi)的概率可近似表示为Pi≈mi/m,i=1,2,…,n。

④ 计算 fi=Pi⋅Δxi,这里 Δxi=xi-xi-1。

⑤在平面直角坐标系中,以[xi-1, xi)为底,以 fi为高(i=1,2,…,n),即可做出样本数据序列{yk},k=1,2,…,m的概率分布直方图.把坐标平面上的点(xi, fi),i=1,2,…,n依次用光滑的曲线连接起来就得到样本数据序列{yk},k=1,2,…,m的概率密度曲线。

1.3 程序设计

样本数据序列的概率密度曲线能够直观地显示出样本数据的概率分布特征。下文用MATLAB 7.0编写程序计算样本数据的概率分布并绘制出样本数据的概率密度曲线。设y为保存样本数据序列的一维数组,n为设定的需要分割的小区间的个数。用MATLAB 7.0编写绘制样本数据序列概率分布直方图与概率密度曲线的函数文件midu.m的代码（略）。

2 算例

样本数据序列有的来自工作与生活中的数据记录,如学生的考试成绩,也有的来自科学实验与理论研究。下文以学生成绩的概率分布和Logistic映射轨道点的概率分布为例,用2.3节的程序midu.m绘制其概率密度直方图和概率密度曲线。

例1.某班98个学生参加期末《统计学》考试的成绩见表1。把2.2节的midu.m文件拷贝到MATLAB的工作目录下,然后,在MATLAB命令提示符后依次输入命令:

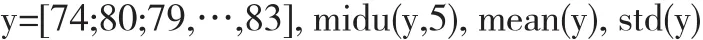
绘制的学生成绩的概率分布直方图和概率密度曲线见图2,计算得到的学生的平均成绩为82.11,标准差为8.38.在图2中,学生成绩被分为5组进行统计。若把学生的成绩分为6组进行统计,只须把上述命令中的midu(y,5)改为midu(y,6)即可,此时,绘制的学生成绩的概率分布直方图和概率密度曲线见图3。比较图2和图3可以看出,对于同一组学生成绩数据,当分组数n不同时,绘制的概率密度曲线的形状也有差异。由图2与图3中绘制的学生成绩分布的概率密度曲线可以看出,该班学生的《统计学》考试成绩分布接近于正态分布。

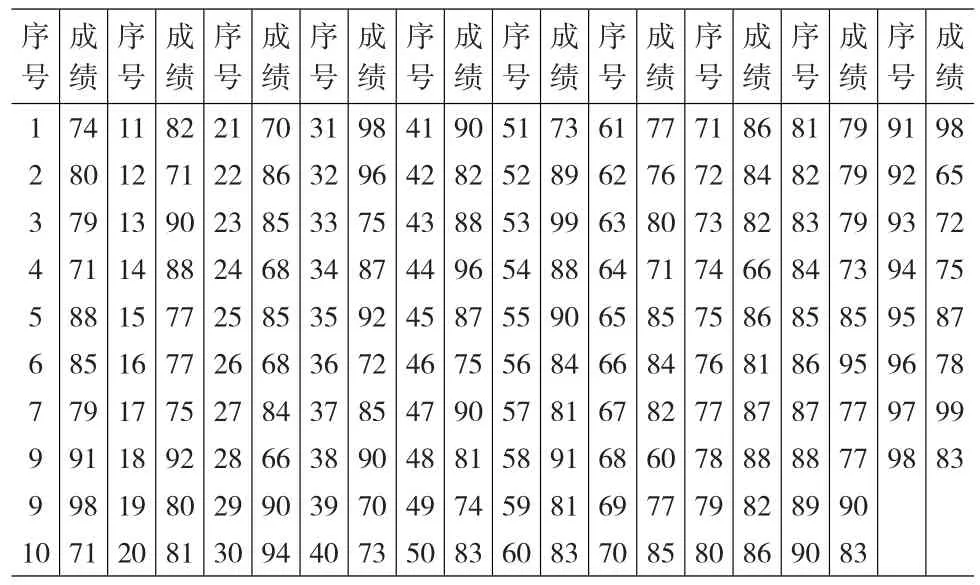
表1 98个学生的《统计学》成绩表

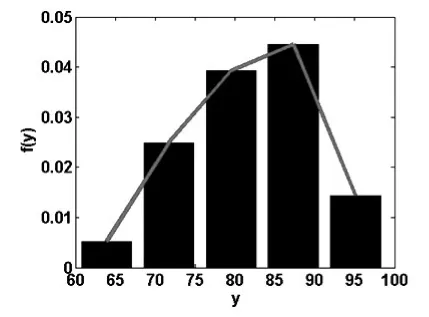
图2 学生成绩概率分布直方图与概率密度曲线(n=5)

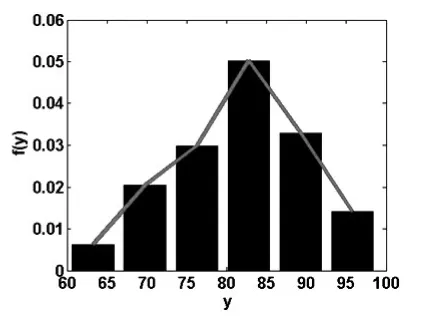
图3 学生成绩概率分布直方图与概率密度曲线(n=6)

例2在生态学中,描述昆虫数目演化规律的Logistic模型可标准化为[4]:

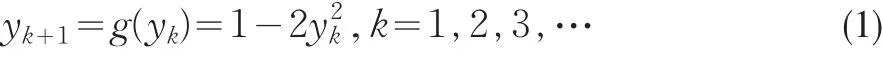
这里g(y)为区间[-1, 1]上的满映射。为研究映射(1)轨道点的概率分布,任取初值 y1=0.1,把映射(1)迭代10000次,取 n=200,映射(1)轨道点 {yk},k=1,2,…,10000的概率分布直方图和概率密度曲线可用附录中的程序Logistic.m绘制,结果见图4。由文[4]知,Logistic映射(1)的轨道点的理论分布概率密度函数为:

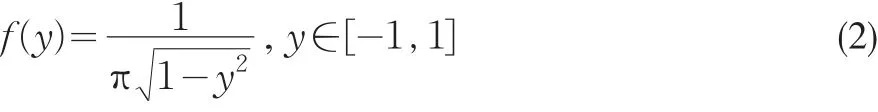
其图像见图5。比较图5与图4可知,图4中由轨道点样本数据绘制的概率密度曲线不太光滑,但图4中由样本数据绘制出的概率密度曲线的形状与图5中的理论概率密度曲线形状基本吻合。

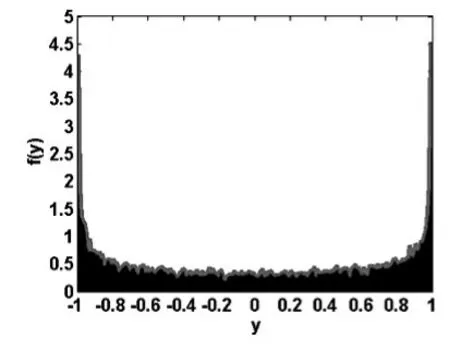
图4 Logistic映射轨道点分布直方图与概率密度曲线

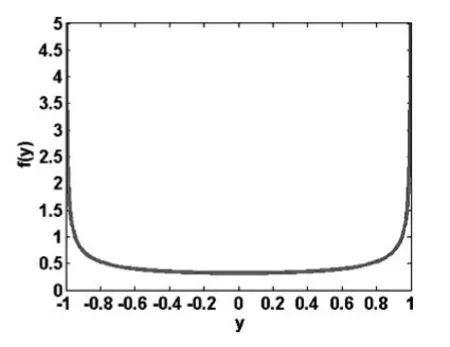
图5 Logistic映射轨道点分布的理论概率密度曲线

3 结论与讨论

本文基于概率论大数定理与微积分微元法,研究了样本数据序列概率分布直方图和概率密度曲线的绘制方法,并给出了相应的MATLAB程序代码。以98个学生成绩的概率分布的计算与Logistic映射轨道演化点分布概率密度的计算为例,用文中给出的MATLAB程序代码进行了仿真实验.由Logistic映射10000个轨道演化点计算出的概率密度曲线与Logistic映射的理论概率密度曲线基本吻合.这证实了本文给出的由本数据绘制概率分布直方图和概率密度曲线的算法和程序的正确性.不足之处是,本文由样本数据序列数据绘制出的概率密度曲线不是很光滑,进一步解决的办法是:一方面可以通过增大样本数据的数量并适当增大分割小区间的个数提高绘制的概率密度曲线光滑度。另一方面,可以引入插值算法进一步提高绘制的概率密度曲线的光滑度。本文给出的由样本数据序列绘制其概率分布直方图和概率密度曲线的程序简单实用,在样本数据量较大时能逼近其真实概率分布。由于许多实际工作与研究中的问题的复杂性,样本数据序列的理论概率分布有时很复杂,或者说根本无法获知,或者获知的成本太大,那么,用本文的方法与程序通过采样数据估计出其近似的概率分布就成为一种很好的研究手段。

[1]张智广.一种利用统计直方图拟合密度曲线的方法[J].内蒙古师范大学学报(自然科学汉文版),2008,37(5).

[2]袁卫,庞皓,曾五一,贾俊平.统计学[M].北京:高等教育出版社,2009.

[3]杨振明.概率论[M].北京:科学出版社,1999.

[4]郝柏林.从抛物线谈起:混沌动力学引论[M].上海:上海科技教育出版社,1993.