头部空腔对固体火箭发动机压强振荡抑制作用的数值研究①

张 峤，李军伟，苏万兴，张 雁，王宁飞

(北京理工大学 宇航学院，北京 100081)

0 引言

不稳定燃烧是固体火箭发动机研制过程中常遇到的棘手问题之一。早期的固体火箭发动机大多用于战术导弹，有50%以上的发动机存在不同程度的不稳定燃烧现象，轻则引起内弹道曲线异常，重则引起发动机爆炸，导致灾难性后果［1］。20世纪70年代开始，为了提高能量，在固体推进剂中加入铝粉等金属燃料，其燃烧产物对高频不稳定燃烧有很强的抑制作用，基本清除了不稳定燃烧现象［2］，之后国内的相关研究工作趋于停滞，国外对战术发动机不稳定燃烧的研究报道也较为罕见。

航天推进、火箭导弹技术的发展对固体火箭发动机提出了高装填、大推力比、初始大推力、低特征信号(采用无铝推进剂)等要求，这对不稳定燃烧的研究提出新课题。国外大型运载火箭的助推器相继使用大型分段式固体火箭发动机。这些发动机的共同特点是轴向长度长、且长径比大(大于10)，装药复杂并存在许多突变截面，段与段之间还装配绝热环［3－5］。

由于声振频率很小，根据经典微粒阻尼理论，颗粒抑制剂粒径须达到几百微米，这是不易实现的。其次，大长径比发动机最显著的特点是极易在内流场中产生旋涡脱落，涡/声耦合、涡/喷管耦合、分布燃烧等诸多增益因素在此工况下作用显著［6－7］。此流场条件下，加入颗粒有时甚至会使得压强振幅加强［8］。因此，传统的微粒抑振理论无法对工程起到充分的指导作用。

近20年来，法国国家空间研究中心(CNES)与法国国家宇航研究院(ONERA)在对大型固体助推器P230的大量点火试验中发现，改变装药结构对改善大长径比发动机中压强振荡效果显著［9－10］。Anthoine等人［11－14］以VKI冷气实验发动机为基础，对潜入式喷管处的涡/声耦合现象进行了大量的实验与数值模拟。研究表明，发动机压强振幅与尾部潜入式空腔的容积成正比，减小装药尾端空腔是减弱压强振荡的方法之一。西北工业大学何国强课题组对此结论也进行了数值与实验验证［15－16］。Blomshield建议设计人员最好不要将燃烧室尾端作为主燃面区域，尾端的复杂燃面容易引发强烈的振荡［17］。近几年中，国内在研的一些型号发现不稳定燃烧后，有的虽然通过将翼柱结构首尾对换的方式解决了压强振荡问题，但仍缺乏足够的理论支持。

综上可知，通过改变药型以改善压强振荡是目前国内外共同关注的课题。国外相关研究大多数集中在尾部容腔［18］，头部装药结构变化对压强振荡的影响规律极少公开报道。本文以此为出发点，采用大涡模拟湍流模型，在VKI冷气实验部分工况的基础上，结合瑞利准则开展数值研究，证实了头部空腔对压强振荡抑制作用的可行性，总结了头部装药结构的抑振规律。

1 计算模型与数值算法

1.1 控制方程及离散格式

通过在傅里叶空间或构型空间将随时间变化的N－S方程进行滤波得到控制方程，滤波函数为

其中，V是计算单元体积。考虑到气体的可压缩性，利用Favre平均对控制方程进行简化:

不考虑化学反应，仅计算单组分工质，滤波后连续方程、动量方程与能量方程为

式中 “—”表示Reynolds平均;“～”表示Favre平均。

将气体工质作理想气体处理，物性参数如表1所示。为简化计算，假设物性参数不随温度变化。

表1 物性参数Table 1 Physical properties for calculation

采用 WALE(Wall－Adapting Local Eddy－Viscosity)亚格子模型［19］，对亚格子应力张量进行封闭。亚格子热通量张量及亚格子尺度粘性力变形功可分别表示为

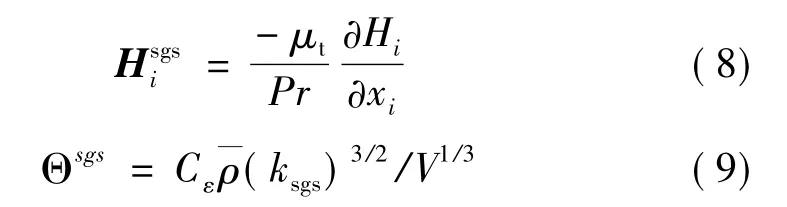
式中 Cε为常数，Cε=1.1。

为了避免中心差分格式产生的数值振荡，连续方程与动量方程采用BCD(Bounded central differencing)格式进行离散，能量方程则采用Power Law格式以加速收敛。时间离散使用二阶隐式欧拉格式，计算步长1 ×10－6s，库朗特数为0.5。

1.2 计算区域

根据VKI实验工况进行建模［11］，基本计算区域如图1所示，发动机长径比约为10。为了更加真实模拟大长径比发动机内流场，发动机采用径向进气。为了产生压强振荡，在距头部0.5 m处安装隔板，以诱发涡/声耦合。旋涡具有强三维特性，虽然轴对称模型不能很好地模拟旋涡拉伸现象，但三维模型计算量太大。文献［20－22］使用二维大涡模拟成功地预估了若干型号发动机的振荡特性。因此，本文仍采用二维轴对称模型。为了更好地识别边界层区域，网格沿径向加密，保证y+≤2。对于各种工况，计算网格数量约为12万。

1.3 边界条件与初始条件

依照VKI实验条件，入口温度T=285 K，入口质量通量=2 kg/(m2·s)，喷喉半径 r=0.015 m。由于气体在拉瓦尔喷管中加速达到超音速，出口截面参数外推求得。以入口静压p=0.18 MPa、入口流速u=1 m/s对流场进行初始化。

1.4 有限元声振型计算方法

声腔模态方程的单元矩阵形式为

式中 ［Kf］为声刚度矩阵;［Mf］为声质量矩阵;{p}为声特征向量;ωa为特征根。

模型表面定义零位移约束。使用有限元法(FEA)求得圆周频率ωa，进而求得声振频率fa。

2 实验对比

2.1 流场特性

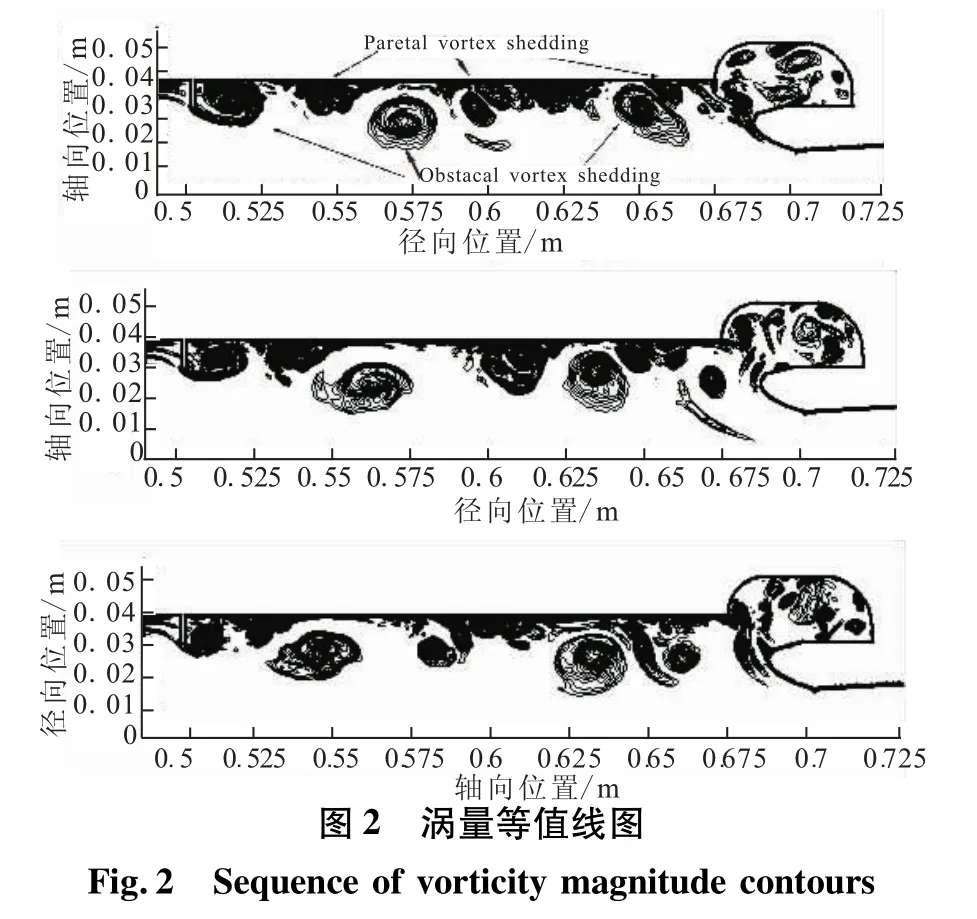
对基本工况进行计算，发动机隔板后侧典型的涡量等值线图如图2所示，每幅图之间间隔2 ms。可看出，由于发动机长径比较大，且存在径向加质，因此存在2种旋涡脱落模式:障碍物旋涡脱落(OVS)与表面漩涡脱落(PVS)。总体而言，脱落的旋涡一部分直接随主流进入喷管被耗散，另一部分撞击喷管头部后，进入潜入式喷管空腔内。潜入式喷管空腔的本质是谐振腔，其内部不断形成的小尺度旋涡可增大流场与声场耦合的几率。虽然流场中的旋涡是2种脱落方式的耦合形式，但PVS的旋涡尺度小于OVS，这些不规则的小尺度旋涡相互融合，之后被与上游脱落的大尺度旋涡吞噬。Anthoine［10］在相应实验中也得出结论:在燃烧室内马赫数较高(大于0.1)工况下，OVS比PVS更能主宰流场的振荡特性。因此，若不考虑PVS产生的小尺度旋涡，可认为隔板与潜入式喷管头部之间始终存在3个大型涡团，故流场具有稳定的周期特性。

2.2 振荡特性

VKI实验［11］测量了发动机头部轴线点的振荡压强，即图1所示点3。将计算所得振荡压强除以当地平均压强，得到无量纲压强振荡曲线，见图3。并将点1计算所得压强、径向速度振荡曲线进行对比，见图4。可看出，压强与径向速度的相位几乎完全一致。

将点3振荡数据进行开窗FFT滤波，无量纲压强谱如图5(a)所示，实验频谱如图5(b)所示。通过将FFT与声有限元振型计算结果进行对比，从表2可看出，这四阶峰值正好对应了燃烧室声腔的前四阶纵向声振频率。对比可知，二维大涡模拟计算结果与实验吻合得较好，可继续采用该方法对振荡特性进行研究。由于声振二阶振幅最大，因此可判断此工况下旋涡脱落频率与声振二阶频率几乎相等，引发了二阶振频为主的强涡/声耦合现象。

表2 VKI实验发动机振荡频率 HzTable 2 Oscillation frequencies in VKI experimental motor

3 抑振方法

大量工程经验表明，将头部装药改成复杂结构，有益于抑制压强振荡。将图1所示结构在头部增加一个类翼槽的容腔，如图6所示。其中，BCDE段设为新增燃面，质量通量与 VKI实验发动机相同。BE连线跨度0.1 m，F点是BE连线中一点，其BF跨度为0.03 m，CD段半径R为0.065 m，该工况为工况1。

对该结构下点1计算所得压强、径向速度振荡曲线进行对比，如图7所示。可看出，压强与径向速度变化趋势不同，相位相差很大。将壁面附近的振荡压强进行FFT变换，并与基本工况进行对比。二阶压强振幅沿轴向的变化规律如图8所示。

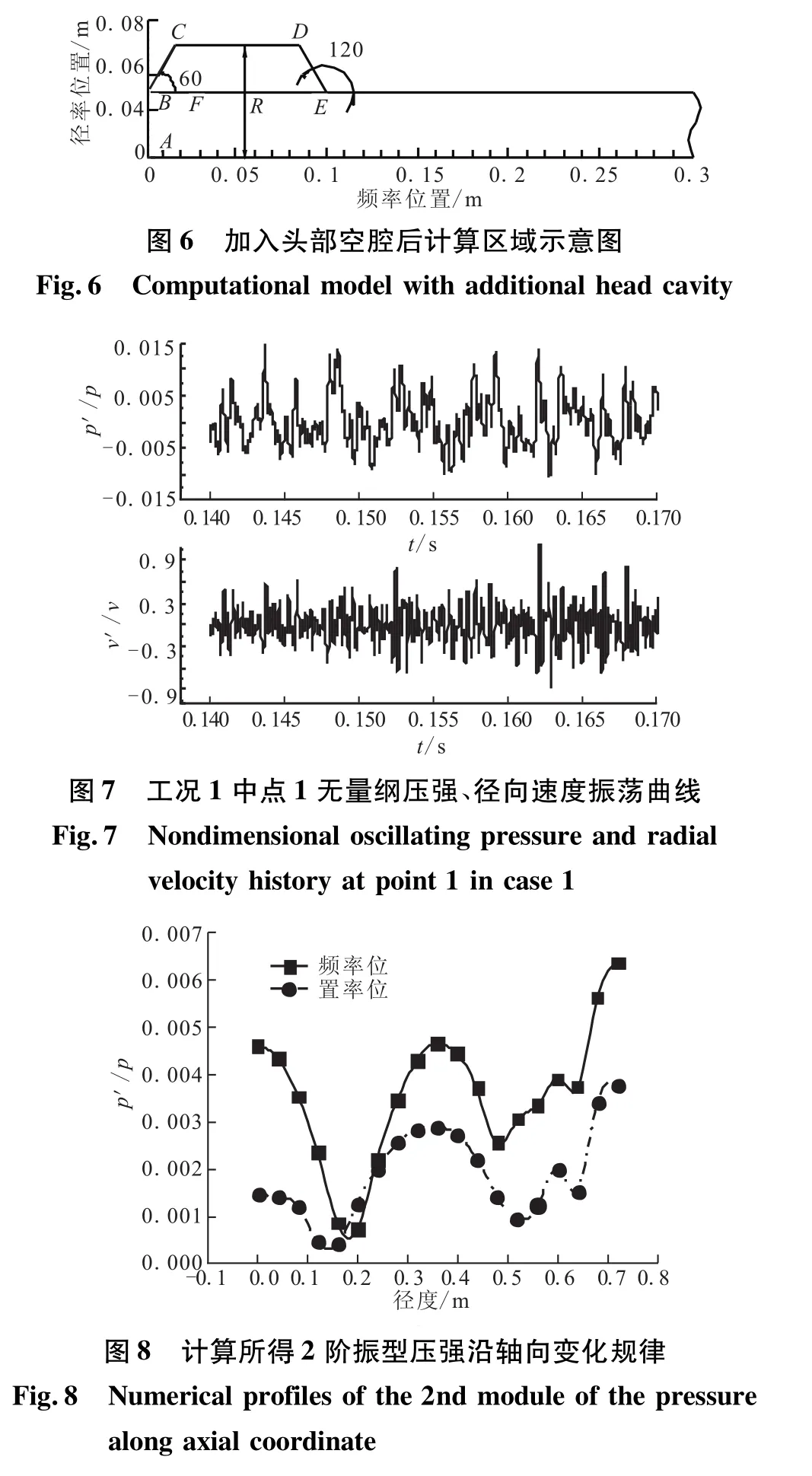
2种工况下，二阶振型均存在3个声压波腹。当不存在头部空腔时，头部与中部声压波腹的振幅基本相等;加入空腔后，头部波腹振幅降为中部振幅的一半。由于尾部在潜入式喷管空腔内，是涡/声耦合的敏感区域，因此在2种工况下，其振幅均大于其余2处波腹。显然，加入空腔后的抑振效果是可观的，3处波腹的无量纲振幅分别下降了67%、38%与41%。

文献［23］认为，这种改变药型抑振的方法是基于增加了装药头部燃面，使得局部质量流率增大所致。作者认为，改变头部药型会带来2个主要变化:增加当地质量流率与增大空腔容积。为了探讨这两个因素对抑振的贡献，必须解耦分析。相对于中部波腹，首尾两处波腹更为重要［24］，此后研究重点关注图1所示点1与点2的振幅规律。

3.1 质量流率的影响

为了研究质量流率的增加对压强振幅的影响规律，仍以图1所示原发动机结构进行计算，并做以下3项对比:

(1)工况2，增大BE段的质量通量;

(2)工况3，重点增大BF段的质量通量，保持FE段的质量通量与原发动机一致;

(3)工况4，保持BE段的质量通量与原发动机一致，将AB段设为新增质量入口。

3种工况中，加质段的总质量流率均与工况1所示BCDE段总质量流率相等。表3所示为各工况下各段质量通量。

表3 工况2～4质量通量Table 3 Mass flux in case 2～case 4

图9为工况2中点1计算所得压强、径向速度振荡曲线，与基本工况相同，压强与径向速度相位基本完全一致。将工况1～4与原发动机振幅进行比较，如表4所示。

表4 不同质量流率工况下压强振幅对比Table 4 Comparison of oscillation amplitudes in different mass flow cases

显然，以上3种方式对压强振荡没有衰减作用，反而会增强其趋势，工况4中的点1振幅变化量高达30%。这说明在药型结构不变的前提下，仅通过改变局部流场结构无法对压强振荡进行抑制。对比工况2～4还可看出，在越靠近声压波腹的区域，加入的质量通量越大，压强振幅增加越显著。

3.2 空腔容积的影响

为了研究头部空腔容积对压强振幅的影响规律，以图5所示结构为基础进行计算，发动机结构进行计算，并做以下3项对比:(1)工况5，将BCDE段全部设置为壁面，该工况下增加的容积比例Vincrease/VVKI=21.87%;(2)工况6，BE段跨度不变，减小CD段半径，使得Vincrease/VVKI=10.94%;(3)工况7，保持图1所示原发动机结构不变，将BE段设置为壁面，此时Vincrease/VVKI=0。

经计算，将工况5～7与原发动机振幅进行比较，如表5所示。可看出，与原VKI发动机相比，工况5、6的压强振幅有所下降，尤其是工况5，振幅较工况1还小。这3种工况下，由于头部的空腔没有径向加质，因此在空腔中容易形成回流区。图10所示为工况7的头部流场。

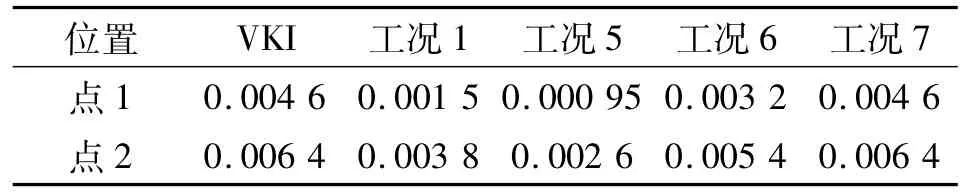
表5 不同空腔容积工况下压强振幅对比Table 5 Comparison of oscillation amplitudes in different cavity volume

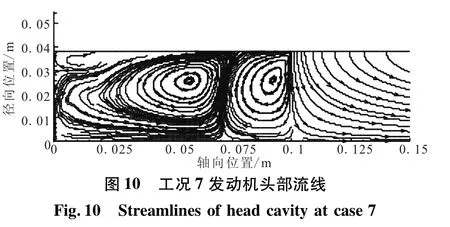
对比该工况与原发动机振幅可知，虽然头部流场结构趋于复杂，振幅却与原发动机完全一致，并未得到衰减，故而压强振幅的衰减并非由头部紊乱的流场破坏发动机声振型所致。可进一步预测出头部空腔体积对抑振的贡献很大，压强振幅随其增大而减小。

3.3 抑振原理

上述初步分析表明，头部的空腔与质量的加入是控制振幅变化的2个相反因素。实际上，这正是著名的瑞利准则的一种表达形式。瑞利准则表述为当压强与放热率或加质率的相位相同时，振荡被加强;相位相反时，振荡被抑制。假设固体火箭发动机声不稳定燃烧中的声波是驻波，瑞利准则可进一步描述为在声压的波腹上进行热或质量交换，可能发生有效的声能增益作用，在声压波峰处注入热量或质量，抑或在声压波谷处抽出热量或质量，振荡将被强化;反之，振荡将会被抑制。由于本文不考虑燃烧放热，仅考虑质量注入，因此在头部引入空腔以及加入燃面，本质上就是在声压波腹处抽取质量与注入质量的综合过程。

考虑到声压波腹在不同时刻可能是波峰，也可能是波谷，因此还必须考察相位问题。装药头部波腹边界上，一个振荡周期T内，压强和速度振荡对系统做的功(ωt+φv)，p0与v0分别为压强与加质速度的零峰幅值，φp与φv分别为压强和速度的相位。经计算，单位时间内，单位声腔边界面积上，振荡对声腔系统做的功因此，当时，振荡有被放大的趋势，当时，振荡有被阻尼的趋势。为了简化处理，将点1的振荡数据代表声压波腹处单位面积上的，并对图4、图7、图9所示各条振荡曲线进行FFT相位提取。计算结果表明，在基本工况与工况2中，振荡速度与压强的相位差仅而在工况1中，相位差高达84°，的范围之内，但显然在此发动机结构下，当装药头部存在空腔时，振荡对声腔系统贡献很小，这正好与工况1中压强振幅减弱吻合。

反观图6可知，距发动机头部0.185 m附近是一声压波节。为了进一步验证瑞利准则的指导作用，以图5所示结构为基础，对在声压波节处加入与抽取质量2种工况进行计算:(1)工况8，在压强波节处设置一跨度为 0.03 m 的重点加质区域，≐8.8kg/(m2·s);(2)工况9，将工况5的BCDE段空腔按其中心位置沿轴向移动到声压波节处。将工况8、9与原发动机振幅进行比较，如表6所示。由表6可看出，这2种工况下压强振幅与原VKI发动机几乎完全一致，没有将振幅明显地放大或缩小。与头部相应结构的工况3、5相比，压强振幅变化极小。由此可推断，在声压波节处进行装药结构改变的意义不大，瑞利准则对固体火箭发动机头部装药抑振设计有较好的指导意义。

表6 声压波腹与声压波节工况下压强振幅对比Table 6 Comparison of oscillation amplitudes in pressure anti-node and pressure node cases

4 规律分析

为了对发动机头部装药的抑振设计做进一步的理论研究，在以上分析基础上，需分别对容腔体积、容腔位置及容腔形状进行分析。每组讨论中包含纯空腔及实际燃面(即空腔壁面注入质量)2种构型。

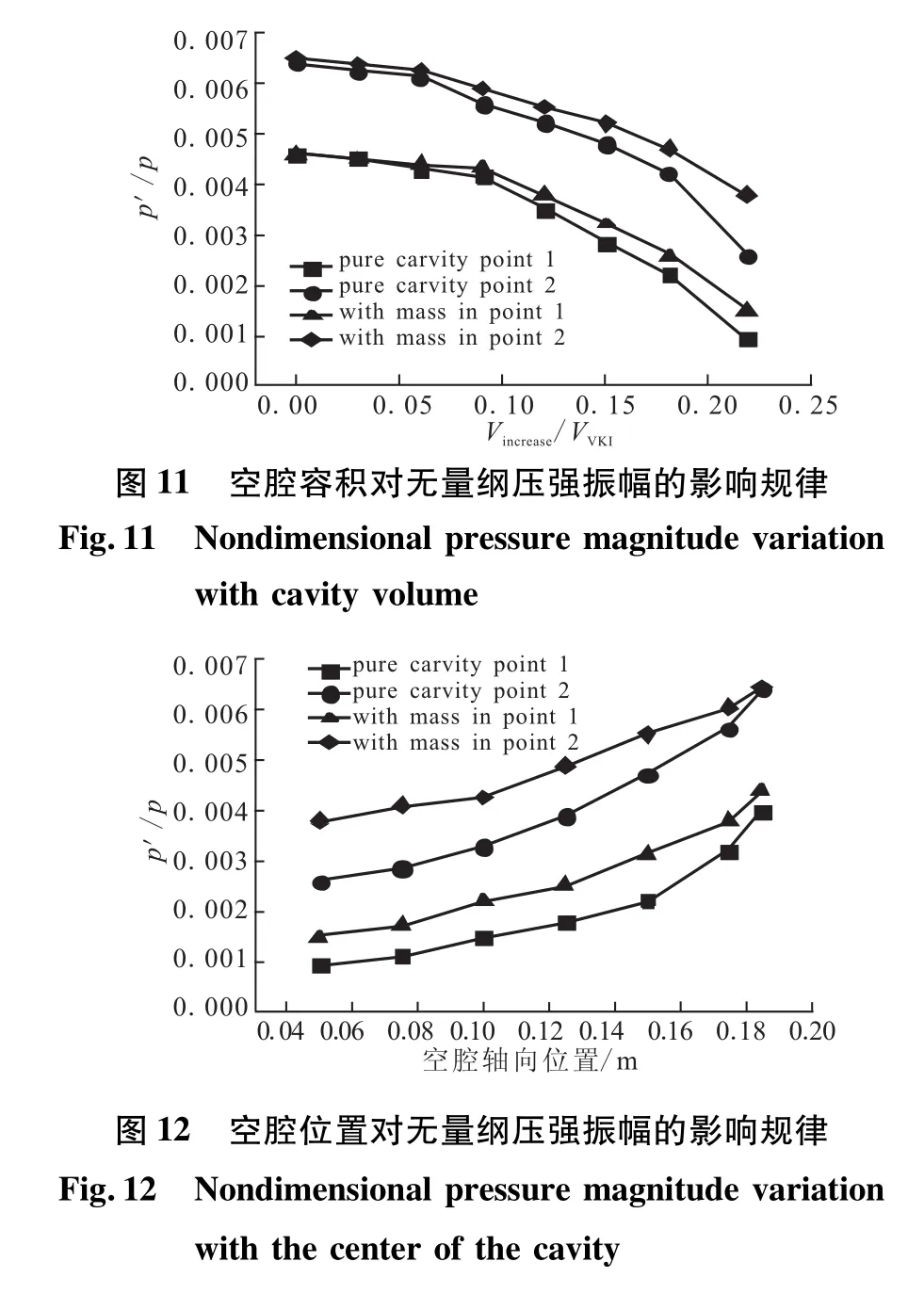
以图6所示结构空腔为基础，分析空腔容积对振幅的影响规律，容积的变化规律与3.2节相同。经计算，无量纲压强振幅随空腔容积的变化规律如图11所示。可看出，压强振荡程度是抽出质量与加入质量2种过程耦合的共同产物。有质量注入的工况下，振幅更大。总体而言，压强振幅随空腔体积的增大而减小，且变化率随着容积的增加而增大。这说明与质量注入相比，空腔的引入对声能的影响更大。

法国科学家在P230试验发动机LP9系列的点火试验［9］中发现，在发动机头部增加空腔，压强振幅反而有增大的趋势，但并未做出解释。分析认为，LP9－n15型发动机增加的头部空腔使得发动机总长度增大，且增大的空腔呈半径增大的突变截面型，故发动机声振频率理应大幅下降［25］。然而，点火试验中提取的振荡频率变化较小，与是否增加空腔关系不大。其次，LP9系列的长径比大，压强振荡是由表面旋涡脱落诱发，所以试验所测振频极有可能不是声振频率，而是表面漩涡脱落频率。表面旋涡脱落的振荡强度随发动机长径比增大而增大，这正与LP9－n15型发动机增加空腔导致长径比增大的趋势一致。因此，这与本文从声学角度出发研究头部空腔的抑振原理不尽相同。

在保持空腔体积与构型恒定的工况下，需进一步就空腔位置对压强振幅的影响进行研究，这对星孔、翼柱装药的开槽位置有着指导意义。由于本文只对头部附近空腔的位置进行研究，故仅将空腔按照其中心从头部平移到第一个声压波节处(距头端0.185 m)。经计算，无量纲压强振幅随空腔中心的变化规律如图12所示。结合3.3节分析可知，在波节处对药型做改动是无意义的，此处压强振幅与原VKI发动机一致。由图12可知，无论有无质量注入，压强振幅均随空腔前移而下降，这进一步证明了此构型中空腔对质量的抽取作用大于新增燃面质量的加入作用，且空腔越靠近声压波腹，质量抽取效果越明显，空腔对声能的阻尼效应越强。

最后，需对空腔形状对振幅的影响规律进行研究，这是对装药设计人员在头部药型开槽长度与深度的选择上有意义的。为了简化计算，在保持图5空腔体积的前提下，将此后所有工况的空腔均简化为圆柱环形结构(即∠CBF=∠DEF=90°)。经计算，无量纲压强振幅随圆柱体宽度(即图5所示BE段，表征装药开槽宽度)的变化规律如图13所示。显然，有无质量注入成为变化趋势的关键点。

当空腔内不存在质量加入时，深而窄的空腔比浅而宽的空腔对压强振幅的抑制更为有效。该结果与瑞利准则相互呼应，说明了越是在靠近声压波腹处集中抽取质量，空腔的抑振效果越佳。其次，随空腔宽度的减小，头部空腔所形成的突变截面与原装药截面相比，半径差别越大。文献［25］的研究结论表明，这将导致声振频率急剧下降。由于下游旋涡脱落频率仅与当地流场特性相关，故旋涡脱落频率变化不大［22］。随声振频率不断减小，涡/声耦合程度下降，也会导致整个系统中的压强振幅减小。

当空腔内存在燃面加质时，压强振幅随空腔宽度的减小、呈先减小、后反弹增大的规律，这正是抽取质量与加入质量相互抗争的表象。当空腔宽度较大时，其深度较浅，对质量的集中抽取效应并不明显，因此振幅较大。随空腔宽度缩小，空腔越靠近声压波腹，空腔的质量抽取效应越强。当宽度为0.055 m时，点1、点2振幅同时达到极小值。这表明在此结构中，当空腔宽度大于0.055 m时，空腔的质量抽取效应大于燃面的质量加注效应。随空腔宽度进一步减小，空腔深度的变化率增大。空腔内部燃面的显著增加，致使极大的质量通量作用于声压波腹处。此时，燃面的质量加注效应远超过空腔的质量抽取效应。因此，空腔的抑振作用大幅度减弱。此变化趋势说明在装药设计中，并非越深的开槽对振幅的抑制作用就好，需根据推进剂和发动机的工作特性，设计合适的深度、宽度尺寸，使得空腔对质量的抽取效应达到最佳。

5 结论

(1)通过改变头部装药结构，进而抑制压强振荡的方法符合瑞利准则。

(2)改变头部装药结构，本质上是质量抽取与注入的相互抗争过程，装药头部复杂流场对抑振基本无效。在声压波节处，改变药型对抑振基本无效;在装药头部声压波腹处，开槽对抑振贡献较大。

(3)压强振幅随头部空腔体积的增大而减小;在声压波腹处，加入的质量通量越大，振幅增加越显著;空腔越靠近声压波腹，空腔对声能的阻尼效应越强。

［1］Blomshield F S.Historical perspective of combustion instability in motors:case studies［R］.AIAA 2001－3875，2001.

［2］De Luca L，Price E W，Summerfield M.Nonsteady burning and combustion stability of solid propellants［M］.Washington DC:American Institute of Aeronautics and Astronautics，1992.

［3］Dotson，K W，Koshigoe S，Pace K K.Vortex shedding in a large solid rocket motor without inhibitors at the segment interfaces［J］.Journal of Propulsion and Power，1997，13(2):197－206.

［4］Mason D R，Folkman S L，Bebring M A.Thrust oscilla－tions of the space shuttle solid rocket booster motor during static tests［R］.AIAA 79－1183.

［5］Prévost M，Le Quellec A，Godon J C.Thrust oscillations in reduced scale solid rocket motors，a new configuration for the MPS of Ariane 5［R］.AIAA 2006－4418.

［6］Gallier S，Godfroy F.Aluminum combustion driven instabilities in solid rocket motors［J］.Journal of Propulsion and Power，2009，25(2):509－521.

［7］王宁飞，张峤，李军伟，等.固体火箭发动机不稳定燃烧研究进展［J］.航空动力学报，2011，26(6):1405－1414.

［8］Ballereau S，Godfroy F.Numerical simulations and searching methods of thrust oscillations for solid rocket motors［R］.AIAA 2006－4425.

［9］Prévost M，Godon J C，Innegraeve O.Thrust oscillations in reduced scale solid rocket motors，part I:experimental Investigations［R］.AIAA 2005－4003.

［10］Chedevergne F，Casalis G.Detailed analysis of the thrust oscillations in reduced scale solid rocket motors［R］.AIAA 2006－4422.

［11］Anthoine J.Experimental and numerical study of aeroacoustic phenomena in large solid propellant boosters－with application to the Ariane 5 solid rocket motor［D］.Universite Libre de Bruxelles＆ von Karman Institute for Fluid Dynamics，2000.

［12］Anthoine J，Bunchlin J M，Guery J F.Effect of nozzle cavity on resonance in large SRM:theoretical modeling ［J］.Journal of Propulsion and Power，2002，18(2):304－311.

［13］Anthoine J，Bunchlin J M，Guery J F.Effect of nozzle cavity on resonance in large SRM numerical simulations［J］.Journal of Propulsion and Power，2003，19(3):374－384.

［14］Anthoine J，Mettenleiter M，Repellin O，et al.Influence of adaptive control on vortex driven instabilities in a scaled model of solid propellant motors［J］.Journal of Sound and Vibration，2003，262(5):1009－1046.

［15］陈晓龙，何国强，刘佩进，等.潜入式喷管对燃烧室中压力振荡的影响［J］.固体火箭技术，2010，33(3):252－255.

［16］吴亚可，何国强，刘佩进，等.潜入式喷管背区空腔对压强振荡及旋涡运动影响的实验研究［J］.固体火箭技术，2010，33(6):621－625.

［17］Blomshield F S.Lessons learned in solid rocket combustion instability［R］.AIAA 2007－5803.

［18］Gallier S，Prévost M，Hijlkema J，et al.Effects of cavity on thrust oscillations in subscale solid rocket motors［R］.AIAA 2009－5253.

［19］Nicoud F，Ducros F.Subgrid－scale stress modeling based on the square of the velocity gradient tensor［J］.Flow，Turbulence and Combustion，1999，62(3):183－200.

［20］Mason D R，Morstadt R A，Cannon S M.Pressure oscillation and structural vibrations in space shuttle RSRM and ETM－3 motors［R］.AIAA 2004－3898.

［21］Zhang Q，Li J，Wang W，et al.Numerical analysis on oscillation characteristics in a tailpipe nozzle solid rocket motor［J］.Journal of Spacecraft and Rockets，2011，48(1):103－109.

［22］张峤，李军伟，王伟臣，等.固体火箭发动机涡声耦合特性数值研究［J］.推进技术，2011，32(3):348－354.

［23］Hu D，He G，Liu P，et al.Study on instable combustion of solid rocket motor with finocyl grain［J］.Journal of China Ordnance，2011，7(1):24－28.

［24］张峤，苏万兴，李军伟，等.固体火箭发动机推力振荡特性数值研究［J］.宇航学报，2011，32(4):835－841.

［25］张峤，李军伟，王宁飞.突变截面燃烧室声腔纵向振荡频率规律分析［J］.航空动力学报，2010，25(7):1653－1658.