亚轨道重复使用运载器总体多学科优化方法①

龚春林，谷良贤，粟 华

(西北工业大学 航天学院，西安 710072)

0 引言

近年来，国际上更加关注运送高度80～100 km、Ma=8～10、设计裕度更宽的亚轨道重复使用运载器(Suborbital Reusable Launch Vehicle，SRLV)［1］。SRLV更强调集成现有技术，总体设计尤为重要。但SRLV的任务和构型均有别于传统运载器，传统飞行器学科相互影响关系将不再适用。因此，传统“专业独立、总体试凑”的运载火箭设计方法在SRLV中面临较大的应用困难。近年来提出的多学科设计优化(Multidisciplinary Design Optimization，MDO)技术以维持学科耦合关系为原则，进行学科协调与系统整体优化设计，可最大程度减少其对经验的依赖性，适合SRLV类创新型复杂系统的总体设计［2］。

Olynick等［3］集成气动热计算、传热分析和弹道数据，对X－33飞行器的全弹道热特性进行了研究，为热防护系统(TPS)设计提供了更准确的依据。Bhungalia等［4］针对美国空军发展的亚轨道可承受响应运输飞行器(ARES)，在进一步耦合气动/热/弹道模型基础上，对相同问题开展了研究。洛马公司Prabhu等［5］研究了亚轨道验证机X－34的静气弹问题，在考虑结构变形的条件下，对X－34飞行器的气动数据进行了修正。研究表明，在SRLV总体设计中考虑多学科耦合是必要的，但现有研究仅对SRLV的少数学科进行综合，导致耦合特征和优化问题均与总体设计内容存在较大差异，其建模、集成和求解过程难以直接应用于SRLV总体设计。

本文针对亚轨道助推器总体设计任务，系统研究了MDO任务规划、建模、集成和求解等方面问题，旨在建立一套完整的、适合SRLV总体设计的新方法，并为缺乏设计经验的其他新型飞行器总体设计提供研究思路。

1 多学科优化任务分析

1.1 基准方案

本文研究的SRLV用作运载火箭助推级，其最大载荷为20 t，要求分离高度不小于80 km，最大飞行速度不小于2 500 m/s。总体基准方案参考飞行任务相似的 X－34 和 ARES［4－5］，如图 1 所示。

气动外形采用“翼+身+垂尾”组合体方案;推进动力用于上升阶段，采用液氧/煤油液体火箭发动机;机身为蜂窝夹层硬壳式结构，通过多个隔框支撑，机翼和尾翼采用多梁式结构;承力结构外铺设被动防热层，驻点、翼面前缘、迎风面、机体侧缘、翼面中心分别采用不同防热材料［4］。

飞行器采用垂直起飞/无动力水平着陆飞行模式，任务剖面分为爬升段、真空滑行段、再入返回段和能量管理段，如图1(d)所示。

1.2 MDO 任务

SRLV总体设计包括外形、弹道、结构、防热、推进等学科。通过这些学科间反复协调和迭代计算，确定以上基准方案的具体参数。

MDO任务是将该设计过程通过严格的数学模型进行描述，并利用数值优化和协调方法，实现主要参数的匹配和寻优。根据总体设计任务，包含学科及耦合关系如图2所示。

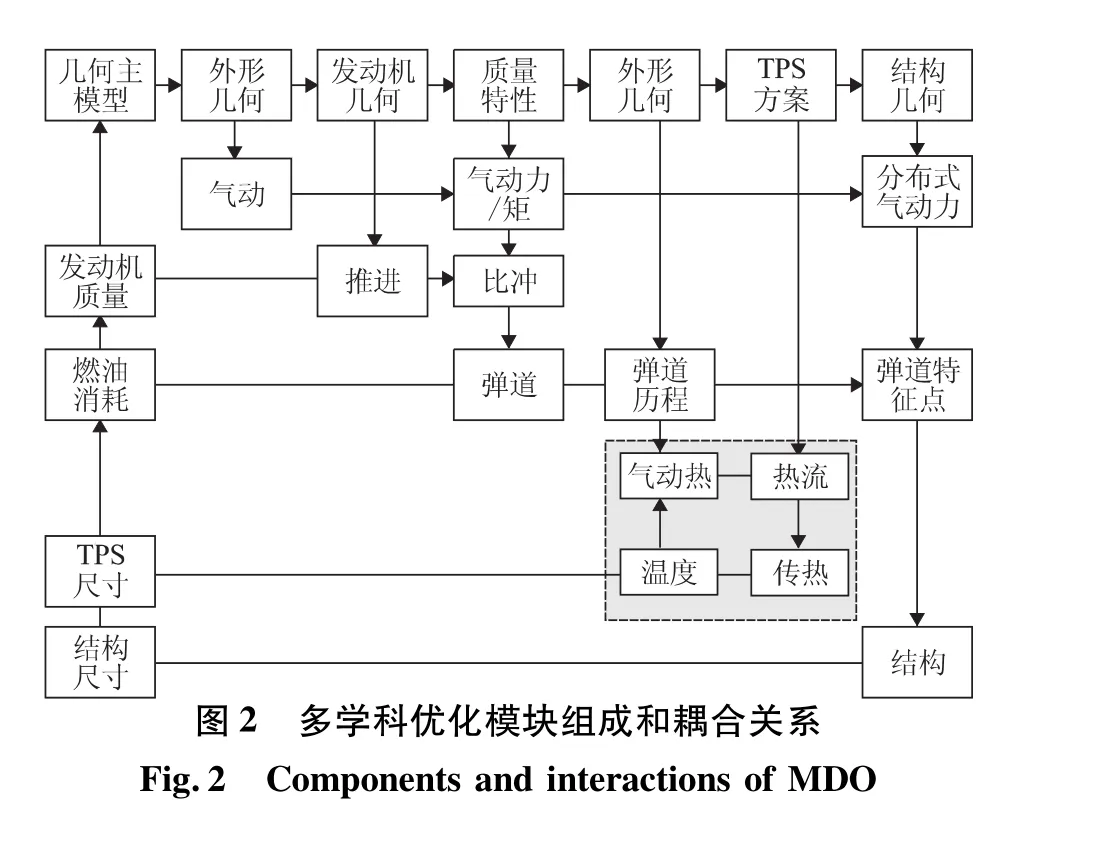
各模块功能如下:

(1)几何主模型。描述SRLV主要几何特征，为各学科提供几何信息，并根据优化器分配的变量或学科反馈信息修改几何参数。

(2)气动。计算飞行包络内的气动性能，为弹道计算提供数据。

(3)推进。计算发动机性能，为弹道提供数据，同时确定发动机质量。

(4)弹道。计算SRLV飞行状态历程，评估飞行任务能力。

(5)气动热。根据弹道历程，计算飞行器表面热流，确定外部热环境。

(6)传热/TPS。计算TPS和结构内部传热，确定全弹道热流和温度变化历程，并确定最优的TPS尺寸返回至主模型。

(7)结构。基于弹道特征点，确定承力载荷，通过调整局部结构参数满足强度和刚度要求，并将最优结构尺寸返回至主模型。

以上模块中，气动热/传热模块间形成子迭代循环，围绕起飞质量的闭合构成顶层循环。通过在外层建立优化目标函数、设计变量和约束，即可构建MDO任务。

2 学科模型

2.1 参数化几何主模型

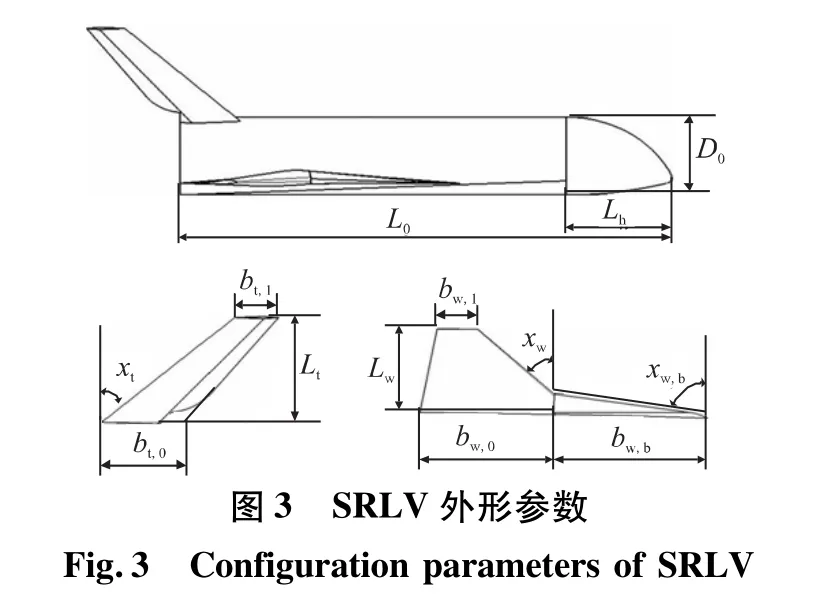
几何主模型在MDO中承担信息枢纽功能，全面表达飞行器的几何特征。采用主模型可将学科之间通信规模由n2降至2n。主模型构造原理可参见文献［6］。基于CAD软件CATIA的建模模块及二次开发接口，建立了具有参数化特征的SRLV主模型，如图1(a)～(c)。其主要外形参数如图3所示。其中，D0、L0、Lh分别为机身直径、长度、头部长度;χw、bw，1、bw，0、Lw分别为机翼后掠角、根弦长、梢弦长、半展长;χt、bt，1、bt，0、Lt分别为尾翼后掠角、根弦长、梢弦长、半展长;χw，b、bw，b为边条翼后掠角和长度。

几何主模型的作用还包括计算飞行器的质量特性。SRLV的起飞总质量为

式中 mp为有效载荷质量;me为设备质量;mF为燃料质量;ms为结构质量;mc为储箱质量;mT为防热层质量。

其中，外形和结构承力件尺寸影响ms，外形和TPS厚度影响mT，燃油消耗量影响mF和mc。

2.2 气动分析模型

气动计算一直是飞行器多学科优化的瓶颈之一，难点是如何权衡效率和精度。本文基于变复杂度方法(VCM)解决，如图4所示。

高速(Ma＞3)阶段的低精度计算采用修正牛顿法，低速(Ma＜3)阶段采用经验工程算法。高精度模型采用Euler方程求解，阻力系数用工程方法修正。在自动优化过程中，高精度模型采用非结构网格，基于动网格技术实现。高、低精度模型的修正采用式(2)。

式中 x为马赫数、攻角、侧滑角等飞行状态参数;f1(x)为低精度气动数据;fh(x)为高精度气动数据;f(x)为修正后的气动数据;σ为校准比例系数。

2.3 推进模型

推进模型包括液体发动机质量计算和性能分析两部分。质量计算采用文献［7］给出的工程估算模型，可确定储箱、气瓶、泵、推力室及附件的质量。性能分析中，推力系数:

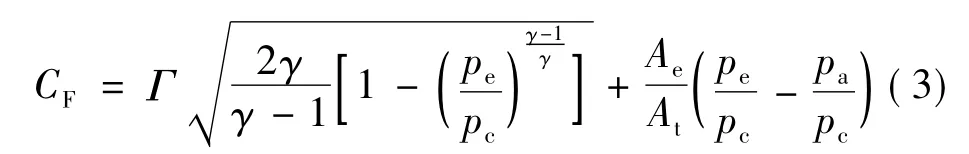
发动机推力:

发动机比冲:

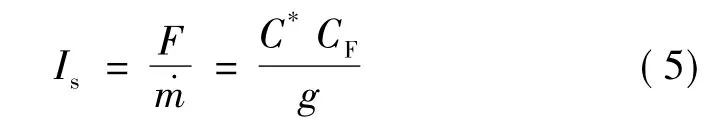
式中 At为燃烧室喉道面积;γ为燃气比热容比;Γ=为喷管出口处的滞止压强;pc为燃烧室压强;Ae为喷管出口面积;m为燃料秒流量;C*为特征速度。

2.4 弹道模型

采用三自由度质点弹道模型，假定飞行器处于“瞬时平衡”状态。弹道模型的关键是制导规律。本文将弹道分为爬升段、真空飞行段和再入段。其中，爬升段又分为2个阶段，0～t1垂直上升段采用俯仰角控制:

t1～t2大气转弯段采用攻角控制:

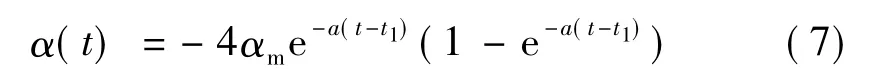
式中 αm为最大攻角绝对值;a是决定攻角变化快慢的系数。

真空飞行段采用俯仰角控制，最优俯仰程序角接近线性关系，即

式中φ0为转弯段结束时的俯仰角;˙φk为俯仰角变化斜率。

再入段需要确定攻角和倾斜角变化规律。倾斜角根据设定的高度－速度曲线计算［8］，攻角变化设计成与马赫数相关的函数:

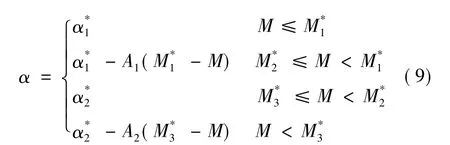
2.5 气动加热模型

采用工程上普遍应用的经验方法确定瞬态热流密度。根据飞行器表面区域加热程度不同，选择不同的经验式［9］。

(1)前缘驻点

采用Fay和Riddle提出的轴对称型驻点气动加热率计算模型:

(2)翼面前缘

采用Rubesin提出的无限后略圆柱和倾斜平板加热综合模型:

(3)机身及其他区域

采用参考焓方法，层流:

其中，边界层外缘参数通过修正牛顿流理论计算。式(10)～式(13)的参数含义参见文献［9］。

2.6 传热/TPS设计模型

该模型用于预测内部传热特征，并确定在使用温度范围内所需TPS尺寸。它与气动热模块密不可分，传热分析以外热流作为输入，外热流瞬态计算则需要根据当前传热分析给出壁面瞬态温度，二者构成紧密的迭代循环，在时间步上交差计算。基于气动热计算和传热分析的TPS设计模型如图5所示。

在传热分析中，假设防热层材料是各向同性的，且仅考虑沿厚度方向的一维热流和温度计算，计算模型如下:

内边界条件:

初始条件:

式中 T为温度;τ为时间;x为沿厚度方向的坐标，x=0为防热层外边界，x=L为结构内边界;qA、qi为外部和内部热流;c、ρ、λ、ε分别为材料的比热容比、密度、导热系数和辐射率;σ为波尔茨曼常数。

由于结构层与防热层材料属性不同，需分层求解以上模型，计算温度和热流变化历程。

2.7 结构模型

结构模型采用有限元方法进行强度分析，并在强度极限范围内最小化结构尺寸。其中，采用 MSC.NASTRAN自带的优化器Sol 200实现结构尺寸优化。与外形相关的结构尺寸由主模型输入，采用录制宏的方法实现有限元网格模型的自动更新。

结构学科内部优化的参数包括机体各舱段蒙皮厚度、承力隔框横截面尺寸、机翼横梁和桁条的截面尺寸、尾翼横梁和桁条的截面尺寸。其中，隔框、横梁、桁条个数均固定不变，间距随外形尺寸变化自动更新。

根据弹道计算结果，选择总载荷最大的弹道点:

根据式(17)获得t时刻所对应的马赫数和攻角，调用气动CFD计算获得面压分布。采用常体积守恒方法(CVT)实现气动/结构网格节点参数的映射，如图6所示。

3 多学科优化问题定义

建立一个非线性规划(NLP)问题需确定目标函数、约束条件和设计变量。MDO问题是各学科优化问题的综合，而不是简单的叠加，既要包括所有学科可能存在的约束和设计变量，又要充分考虑潜在的学科冲突，避免“过约束”和“非独立设计变量”［6］。

3.1 目标函数

选取满足给定任务条件下的最小起飞质量m0作为目标函数。由于SRLV所需起飞质量因执行任务不同而异，本文选取代表设计极限情况的飞行任务，即载荷最重/分离点最高/分离速度最大的情况。

3.2 设计变量

SRLV总体方案可优化的变量包括几何、推进、弹道、结构、防热5个学科。其中，由于传热/TPS学科采用迭代法确定最优TPS厚度，结构学科内部完成结构尺寸优化。因此，系统级优化不包括这些变量。最终选择如下影响主要总体性能的变量:

(1)几何学科变量。选择对气动性能和气动加热特性起主要影响的参数，如图3所示。包括机身直径D0、机身长度 L0、头部长度Lh、机翼面积Sw、前缘后掠角 χw、根梢比 ηw、展弦比 λw、垂尾面积 St、展弦比 λt、根梢比ηt和后掠角χt。

(2)推进学科变量。推力室平均压强 pc、燃料总量mf、单台发动机地面推力大小F0、喷管喉径Dt、喷管膨胀比ε、喷管膨胀角θe。

(3)弹道学科变量。主要是制导规律参数，其中，上升段和真空段参数αm、a、t1、t2和˙φk影响飞行器的运载能力，再入段参数 α1*，α2*，M1*，M2*，M3*，A2影响再入过载、动压和气动加热特性。

3.3 约束条件

总体设计主要关心的约束条件如下:

(1)气动学科

最大轮廓尺寸限制;

具有足够的内部容积;

升阻特性约束。

(2)推进学科

正常工作时，出口压强与外界压强满足pe/pa≥0.3;

喷管扩张比ε、喉径Dt以及发动机外径D0之间的几何约束;

发动机结构质量约束。

(3)弹道学科

载荷分离速度v＞2 500 m/s;

载荷分离高度h＞80 km;

载荷分离弹道倾角25°≤θ≤35°;

再入最大动压＜40 kPa;

再入最大过载＜5 gn;

再入最大热流率˙qmax≤400 W/m2。

(4)热防护学科

舱内最大温度Tmax≤150°;

防热结构质量约束。

(5)结构学科

强度方面，材料剩余强度系数不小于1.5;

刚度方面，翼尖最大变形量不超过翼展的5%;

结构质量约束。

从多学科角度，以上约束条件存在较大的冗余，需要消除。其中，升阻特性可通过弹道计算;发动机结构、防热结构、机体结构质量约束均已包含在目标函数中;弹道学科的热流率约束和舱内最大温度约束可由TPS设计自动满足;过载约束、强度、刚度约束在结构学科的内部优化过程中自动满足;综合可得MDO系统级约束为7个。

4 系统集成与优化

4.1 系统集成与求解策略

MDO问题的集成需要选择一定的优化计算构架组织优化问题，如MDF、CO、CSSO等。根据图2所示的设计结构矩阵，学科间迭代循环是质量平衡，属于典型的耦合密集问题，因此本文选择多学科可行方法MDF。其中，多学科分析(MDA)采用固定点迭代方法(FPI)。按照上节定义的MDO问题。

在软件框架FIPER/iSight－FD中集成各学科计算模块，建立学科任务流和数据映射关系。

MDO的优化算法选择也很重要。非梯度算法不依赖于初值点选择，具有全局收敛特性，但优化过程需大量迭代，计算效率非常低;而梯度算法虽对初始值和导数信息非常敏感，易陷入局部最优，但需迭代次数少，收敛速度快。考虑到SRLV较大的迭代计算规模，选择求解效率较高的梯度算法(SQP)求解。

4.2 结果分析

在包含28个CPU(4核，共112个计算节点)的刀片计算服务器上执行该多学科优化任务，算法迭代68次，耗时约173 h。其中，主要计算工作量在于图4所示的基于Euler方程的气动学科分析，并行执行模式下，计算一个状态需1～2 h。

优化迭代历程如图7所示，优化结果如表1所示。

表1 SRLV多学科优化结果Table 1 Multidisciplinary optimization results of SRLV

优化后改变主要表现在以下方面:

(1)机身和头部长细比增加、机翼面积增加，升阻比提高，阻力减小约3%，减小了阻力燃油消耗;

(2)发动机喷管扩张比增加和室压增加提高了比冲，由初始的2 834.3 N·s/kg提高至2 872.4 N·s/kg，但发动机结构质量略有增加;

(3)起飞推力增大、比冲增加、阻力减小以及上升段弹道参数的优化，共同促使燃油消耗量下降5.2%左右;

(4)由于整个机体变得更加细长，气动加热略为严重，防热层质量增加;

(5)通过结构尺寸参数优化，结构质量有所减少，约320 kg。

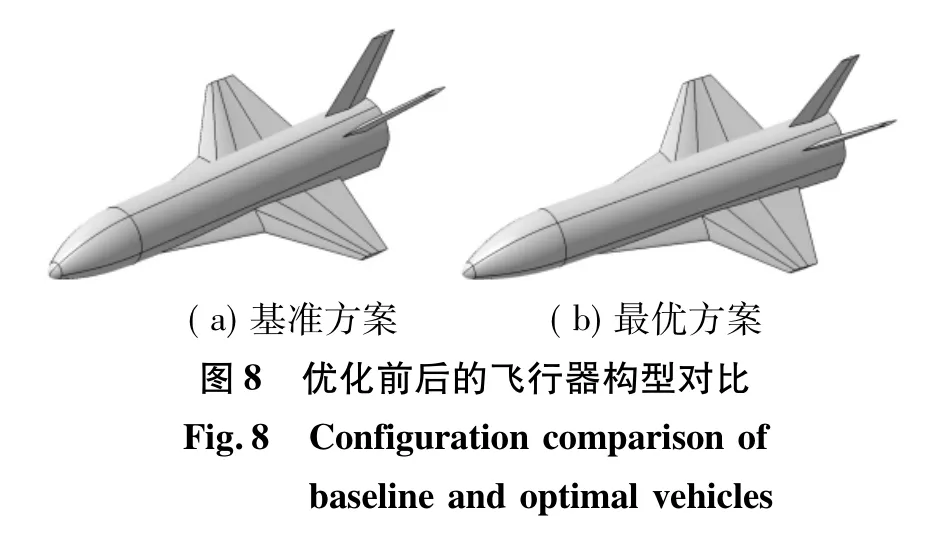
以上各方面的综合作用，使得优化后方案在约束要求的范围内起飞总重减小约2.4%。优化前后飞行器外形如图8所示。

5 结论

(1)SRLV总体设计涉及学科广，约束条件多且存在冲突性，必须在大范围设计空间内采用MDO手段进行权衡。

(2)MDO体现了各学科权衡的过程，其结果并非学科最优的叠加。本文优化结果中，虽然发动机和防热系统质量均有所增加，但这些改变能带来更大的燃油节省量，同时机体结构质量下降，因而从系统目标上是最优的。

(3)采用MDF构架组织多学科优化问题是可行的，但优化算法选择对结果有较大影响，需要结合实际问题进行权衡。

虽然本文在气动、结构学科采用了数值计算模型，但受限于计算能力和网格自动化能力，这些模型均作了较多简化。对该类新型飞行器有必要建立逼真度和计算精度更高的模型，以更加准确地把握学科间耦合关系和提高整体优化性能。

［1］Martin J C，Law G W.Suborbital reusable launch vehicles and applicable markets［M］.Washington D C，U S.Department of Commerce Office of Space Commercialization，2002.

［2］Alexandrov N.Editorial－multidisciplinary design optimization［J］.Optimization and Engineering，2005，6(1):5－7.

［3］Olynick D.Trajectory based TPS sizing for an X－33 winged vehicle concept［R］.AIAA 1997－276.

［4］Bhungalia A A，Beran P S.Hypersonic aerothermodynamics TPS design，analysis and optimization:affordable responsive space－lift(ARES)booster case study［R］.AIAA 2006－7124.

［5］Prabhu R K.Summary report of the orbital X－34 wing static aeroelastic Study［R］.NASA－CR－2001－210850，Hampton，Virgina，USA:NASA，2002.

［6］龚春林，谷良贤.面向飞行器多学科设计优化的主模型技术［J］.宇航学报，2009，30(3):914－918.

［7］休译尔D K.液体火箭发动机现代工程设计［M］.朱宁昌，等译.北京:中国宇航出版社，2004.

［8］闫晓东，唐硕.亚轨道飞行器返回轨道设计方法研究［J］.宇航学报，2008，29(2):467－471.

［9］Tauber M.A review of high－speed，convective，heat－transfer computation methods［R］.NASA－TP－2914，Hampton，Virgina，USA:NASA，1989.