两条参数曲线间的Hausdorff距离的研究

李英明，李旭健

（1．莱芜职业技术学院 信息工程系，山东 莱芜 271100；2．山东科技大学 信息科学与工程学院，山东 青岛 266510）

两条参数曲线间的Hausdorff距离的研究

李英明1＊，李旭健2

（1．莱芜职业技术学院 信息工程系，山东 莱芜 271100；2．山东科技大学 信息科学与工程学院，山东 青岛 266510）

在几何设计中，两个几何体间的Hausdorff距离是一种非常有用的度量方式，但是其计算通常而言相当耗时．本文找到了一种有效快捷的计算二维平面或三维空间中两条参数曲线的Hausdorff距离的新算法，并通过若干例子展示了它的有效性．

Hausdorff距离；参数曲线；算法

两条曲线间的Hausdorff距离被广泛应用于几何设计当中，如样条曲线曲面的近似隐式化，代数曲线曲面近似参数化，代数曲线曲面拟合、以及图像匹配识别等［1－2］．然而，Hausdorff距离的计算却相当困难，并且通常相当费时，它的研究也只局限在某些特定的场合下．Sedergerg［3］提出了两条平面曲线的Hausdorff距离的范围的计算方法．在此基础上，Jüttler将其拓展到可以计算两条平面隐式或参数曲线间 Hausdorff距离的范围．文献［4－7］中提出了圆锥曲线与参数有理Bézier曲线间近似Hausdorff误差的方法．目前，两条二维或三维空间中曲线间近似Hausdorff距离的算法的研究却很少．为了提高Hausdorff距离的计算效率，减少计算时间，本文提出了一种有效的计算两条二维或三维空间中曲线间近似Hausdorff距离的算法．与精确计算方法相比，该近似算法效率高，速度快，计算精度可控，满足实用要求．

1 Hausdorff距离的定义及几何意义

给定两条参数曲线P（s），Q（t），t0≤t≤t1，假设两条参数曲线的末端端点重合，即

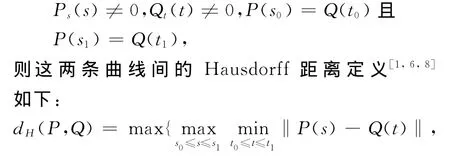
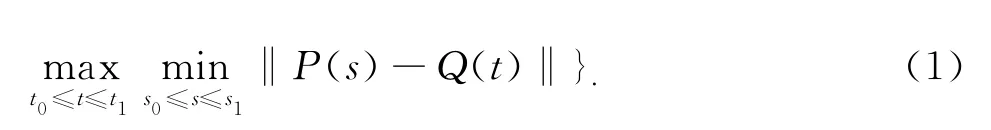
为了计算它们之间的Hausdorff距离，定义一个两条曲线间距离函数的平方项的映射，如公式2所示：

对于两条正则参数曲线P（s）以及Q（t），有两个原因使得

fs（s，t）＝0，即

1）P（s）＝Q（t），即两条曲线相交；

2）Ps（s）垂直于P（s）－Q（t）．

类似地，同样有两点使得ft（s，t）＝0，即

1）P（s）＝Q（t），两条曲线相交；

2）Qt（t）垂直于P（s）－Q（t）．

下面的引理1是简化Hausdorff距离的计算．

引理1 两条曲线P（s）及Q（t）间的Hausdorff距离可以通过两条曲线fs（s，t）＝0和ft（s，t）＝0间的交点求出，即

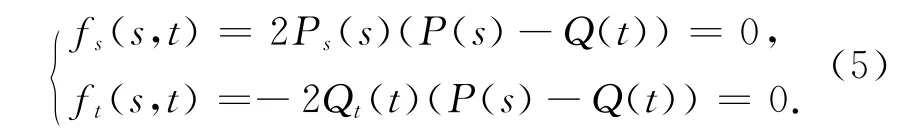
证明 等式fs（s，t）＝0隐式定义了s－t平面上的一条曲线．假设这条曲线的显式表达式为

s＝s（t），t0≤t≤t1，且s0＝s（t0），s1＝s（t1）．

约束方程（2），即f（s，t），在上述曲线fs（s，t）＝0上，可以得到单变量t的函数，也就是f（s（t），t），t0≤t≤t1，固定t＝＾t，使

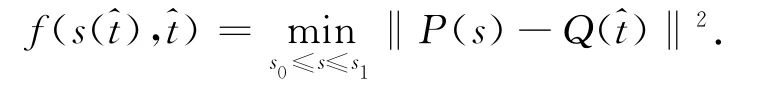
由于在两个端点，有f（s（t0），t0）＝f（s（t1），t1）＝0，以及f（s，t≥0），0，（s，t∈ ［s0，s1］× ［t0，t1］），所以函数f（s（t），t）的最大值点必然出现在其局部极值点，即

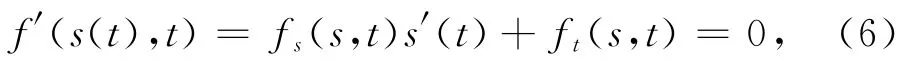
因为函数f（s，t）限制在曲线fs（s，t）＝0（公式（6））上，所以可以得到

引理1意味着，如果两条曲线P（s）与Q（t）之间的Hausdorff距离可以在它们的交点（sa，ta）处达到，那么有向量P（sa）－Q（ta）同时垂直于向量P＇（sa）与向量Q＇（ta）（参见图1）．

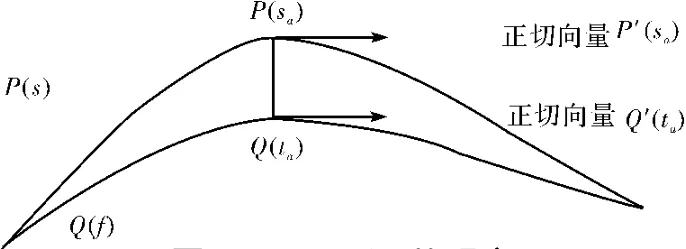
图1 Hausdorff距离Fig．1 Hausdorff distance

图1中如果｜P（sa）－Q（ta））｜为 Hausdorff距离，则向量｜P（sa）－Q（ta））｜同时垂直于向量P＇（sa）与向量Q＇（ta）．

2 简化与运算

曲线fs（s，t）＝0以及ft（s，t）＝0均为隐式的．在通常情况下，它们的形状非常复杂，所以它们的交点也同样非常复杂．但大多数情况下两条曲线P（s）以及Q（t）都满足一条简单的性质，而这条性质使得fs（s，t）＝0与ft（s，t）＝0的求交运算变得较为容易．这种性质可表示成如下引理2．

引理2 1）穿过任意点Q（t）并且垂直于该点的切向Q＇（t）的直线，如果其与曲线P（s）仅相交于唯一点，那么在区域［s0，s1］× ［t0，t1］，存在曲线ft（s，t）＝0的非自交连续分支，并且该分支包含（s0，t0）以及（s1，t1）；

2）穿过任意点P（s）并且垂直于该点的切向P＇（s）的直线，如果其与曲线Q（t）仅相交于唯一点，那么在区域［s0，s1］×［t0，t1］，存在曲线fs（s，t）＝0的非自交连续分支，并且该分支包含（s0，t0）以及（s1，t1）．

证明 这里仅证明1），2）的证明与1）是完全相似的．引理中的条件，即穿过任意点Q（t）并且垂直于该点的切向Q＇（t）的，且与曲线P（s）仅相交于唯一点的直线，意味着，对于任意直线t＝ta，ta∈［t0，t1］与曲线ft（s，t）＝0，（s，t）∈ ［s0，s1］× ［t0，t1］相交于唯一点．另一方面，因为P（s0）＝Q（t0）以及P（s1）＝Q（t1），ft（s0，t0）＝ft（s1，t1）＝0，也就是，点（s0，t0）和（s1，t1）均落在曲线 ft（s，t）＝0上．

下面，利用反证法证明曲线ft（s，t）＝0在分支为连续的．

假设曲线ft（s，t）＝0，（s，t）∈ ［s0，s1］×［t0，t1］在上述定义域中非连续．非连续性会导致两种情况，或者直线t＝ta与曲线ft（s，t）＝0（参见图2（a））无交点，或者两者之间多于一个相交点（参见图2（b），2（c））．第一种情况意味着穿过点Q（ta）且垂直于与该点的切向Q＇（ta）的直线，与曲线P（s）无交点．第二种情况则意味着直线将会与曲线P（s）有多于一个交点．两种情况都将导致矛盾的产生．所以假设不成立．即曲线的连续性得到证明．

然后，假设曲线ft（s，t）＝0在［s0，s1］× ［t0，t1］分支是自交的．参照图2（d），这种自相交的情况会使得穿过点Q（ta）且垂直于该点切向Q＇（ta）的直线，与曲线P（s）有多于一个交点．这同样会导致矛盾．

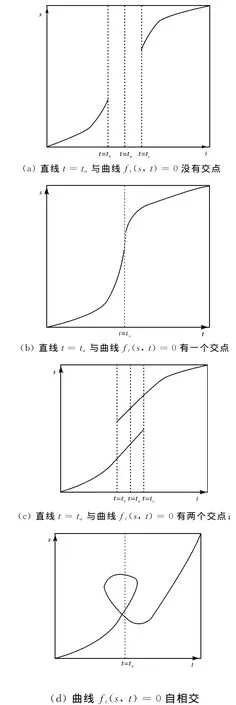
图2 不连续性与自交Fig．2 Discontinuity and intersects with itself

因此，在区域［s0，s1］× ［t0，t1］，存在一个连接点（s0，t0）与点（s1，t1）的曲线ft（s，t）＝0的非自交连续分支，引理2得证．

根据引理1，两条曲线 P（s）与 Q（t）间的Hausdorff距离可以在曲线l1：fs（s，t）＝0与l2：ft（s，t）＝0的交点处达到．如果两条曲线P（s）与Q（t）满足引理2的条件，则存在l1与l2在（s0，t0）以及（s1，t1）上的非自交连续分支，因此，l1与l2的交点可通过追踪它们其中的一条计算求得．

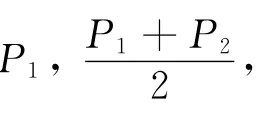
算法1：计算两条曲线间的Hausdorff距离输入：两条曲线P（s）以及Q（t），追踪步长ε．输出：P（s）与Q（t）间的近似Hausdorff距离．1：当追踪隐式曲线fs（s，t）＝0，可以得到一个点集序列｛（si，ti），i＝0，1…，n｝；2：for i＝0to n－1do 3：用 P1＝ （si－1；ti－1）和 P2＝ （si，ti）代入ft（s，t）；4：if ft（s；t）的符号变化 （说明这两点之间有交点）then 5：选择P1，P2，P1＋P22 三者之一作为交点，在该点处f2s（s，t）＋f2t（s，t）取最小值；6：end if 7：end for 8：将所有的交点代入f（s，t），最大值可被认为是近似的Hausdorff距离．

追踪隐式曲线的方法有多种［9］，这里选择正负法［10］．

下面来分析这种近似估算Hausdorff距离的精确程度．假设近似的Hausdorff距离出现在点A＝（sa，ta）处，而真实的Hausdorff距离出现在点B＝ （sb，tb）处，连接这两点间的线段被记为L，即

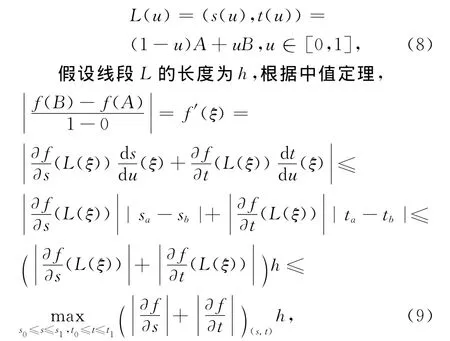
其中，ξ∈ ［0，1］，算法1输入的追踪步长ε可被认为（9）式中的h，用于估计近似Hausdorff距离的精确程度．

下面用两个实例来解释说明算法1的效率．

例1 如图3所示，计算两个平面Bézier曲线P（s）以及Q（t）间的Hausdorff距离．两个平面三次Bézier曲线的控制顶点如下：

P（t）：（0，0），（1，1），（2，1），（3，0）；

Q（s）：（0，0），（1，2），（2，2），（3，0）；

通过算法1，可以得到这两条三次曲线的近似的Hausdorff距离，也就是0．75，在曲线P（s）上点（1．5，0．75），与曲线Q（t）上点（1．5，1．5）之间．这个例子的计算时间为0．1749s．

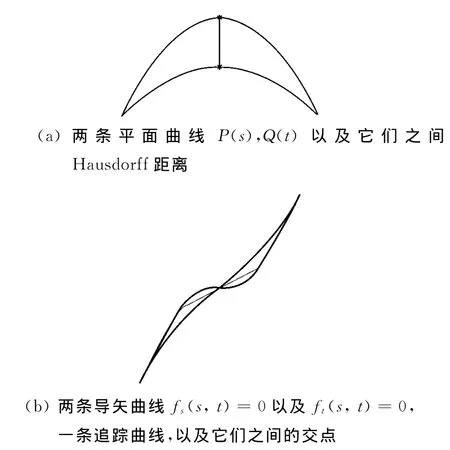
图3 计算两条平面三次Bézier曲线间的Hausdorff距离Fig．3 Calculation of theHausdorff distance between two planar cubic Bézier curves

例2 如图4所示，要处理两条空间四次Bézier曲线P（s）以及Q（t）．其控制顶点如下：

P（s）：（0，0，0），（1，1，－1），（2，1，1），（3，－1，－1），（4，0，0）；

Q（t）： （0，0，0）， （1，0．5，－ 0，5）， （1．5，－0．5，0．5），（3，－1，－0．5），（4，0，0）．

两条曲线间的近似Hausdorff距离是0．7141，对应 于 曲 线 P（s）上 的 点 （1．6818，－0．2614，－0．0641）， 以 及 曲 线 Q（t） 上 的 点 （2．000，0．3750，－0．1250）．在这个例子中，算法1需要的时间为0．1969s．

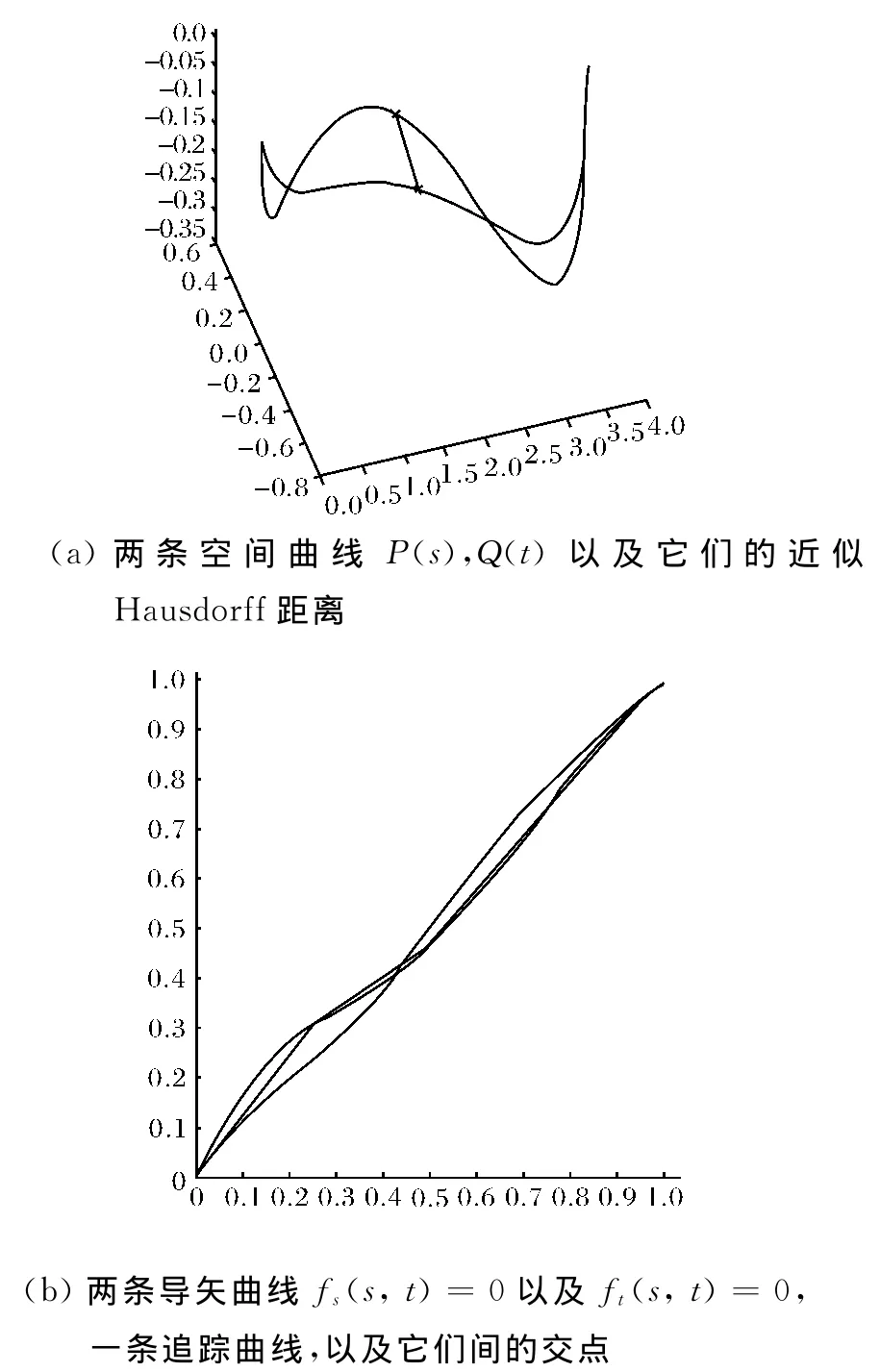
图4 计算两条空间四次Bézier曲线间的Hausdroff距离Fig．4 Calculation of the Hausdorff distance between two space quartic Bézier curves

3 结束语

本文提出了一种计算两条平面或者空间曲线的近似Hausdorff距离的方法．构造了两条曲线间的距离函数，并且证明了两条曲线间的Hausdorff距离一定会在这两条曲线的偏导曲线的交点上达到．然后，通过追踪一条偏导曲线来寻找交点，确定近似Hausdorff距离达到的点的位置，并通过若干个例子验证了本文算法的效率与准确性．此算法为Hausdorff距离的应用提供了新的思路．

［1］Jäuttler B．Bounding the Hausdorff distance of implicitly defined and／or parametric curves［C］／／Lyche T，Schumaker L L．Mathematical Methods in CAGD：Oslo 2000．Nashville：Vanderbilt University Press，2001：223－232．

［2］刘嘉敏，王 玲，兰逸君，等．基于外耳轮廓边缘信息的人耳识别［J］．计算机辅助设计与图形学学报，2008，20（3）：337－342．

［3］Sederberg T W．Planar piecewise algebraic curves［J］．Computer Aided Geometric Design，1984，1：241－255．

［4］Ahn Y J．Conic approximation of planar curves［J］．Computer Aided Design，2001，33（12）：867－872．

［5］Ahn Y J．Helix approximations with conic and quadratic bézier curves［J］．Computer Aided Geometric Design，2005，22：551－565．

［6］Floater M．High order approximation of conic sectons by quadratic splines［J］．Computer Aided Geometric Design，1995，12：617－637．

［7］Floater M．An O（h2n）Hermite approximation for conic sectons［J］．Computer Aided Geometric Design，1997，14：135－151．

［8］Degen W L F．Best approximations of parametric curves by spline［C］／／Lyche T，Schumaker L L．Mathematical Methods in CAGD II．New York：Academic Press，1992：171－184．

［9］Shou H，Shen J，Yoon D．Robust plotting of polar algebraic curves［J］．Space Algebraic Curves，and Offsets of Planar Algebraic Curves Reliable Computing，2006，12（4）：323－335．

［10］Yu Z，Cai Y，OH M，et al．An efficient method for tracing planar implicit curves［J］．Journal of Zhejiang University SCIENCE，2006，A7：1115－1123．

Abstract：In geometric design，the Hausdorff distance between two geometric entities is a useful measurement，while its computation is usually very time consuming．This paper，presents a new effective method to compute the Hausdorff distance between two parametric curves in 2Dplane or 3Dspace，and shows its effectiveness by some examples．

Key words：Hausdorff distance；parametric curve；algorithm

The study of the Hausdorff distance between two parametric curves

LI Yingming1，LI Xujian2
（1．Department of Information Engineering，Laiwu Vocational and Technical College，Laiwu，Shandong 271100；2．College of Informatics Science ＆Engineering，Shandong University of Science and Technology，Qingdao，Shandong 266510）

TP301

A

1000－1190（2012）03－0270－05

2011－09－07．

国家863重点课题基金项目（2009AA062701）；山东省高等学校优秀青年教师国内访问学者项目经费资助；莱芜职业技术学院项目经费资助．

＊E－mail：lwaming＠163．com．