一种虚拟人追逐过程中的情绪博弈模型

卞玉龙，刘箴

(宁波大学信息科学与工程学院，浙江宁波315211)

人的行为模型［1-2］是虚拟仿真领域的一个热门方向，特别是人类行为博弈［3］的研究，仍是具有挑战性的课题.实际上，已有的博弈理论大多考虑人类决策中的理性因素，而实际上人的决策也受情绪的影响，是理性和情绪因素综合的过程.人类的追逐行为是一种常见的博弈行为，体现了体力和心理的较量，对于追逐行为模型系统性的研究至今尚未见其相关文献.目前在虚拟仿真领域中的追逐模型仍未考虑虚拟人的生理和心理因素，追逐行为的表现难以令人信服.本文结合已有的行为动画研究［4-13］，重点研究绕障碍物追逐的虚拟人行为模型，充分考虑了情绪因素对虚拟人的追逐行为的影响，并结合人体生物力学原理、环境心理学原理和物理学原理，建立了人体的情绪模型、速度模型和体力模型;根据非合作动态博弈原理提出了情绪影响人的行为和决策的算法，并根据算法进行模拟仿真，验证了该算法的合理性.

1 虚拟人的情绪博弈分析

根据心理学和人工智能科学［14-15］研究，虚拟人的认知结构设计如图1所示.首先通过各种感知器官接收环境中的各种刺激，然后将刺激传入大脑，大脑经过处理后产生情绪［16］.情绪可以影响人的决策，也可以直接影响人的行为.例如，人在激动的时候就很难做出合理的决策.行动后的结果通过感知器官再次传入大脑，影响人的情绪.

根据OCC情绪理论，被追者的情绪类型来自于对事件(追逐事件)、对象(圆柱体)和追逐者的评价，所产生的情绪是对被追者最有利的.

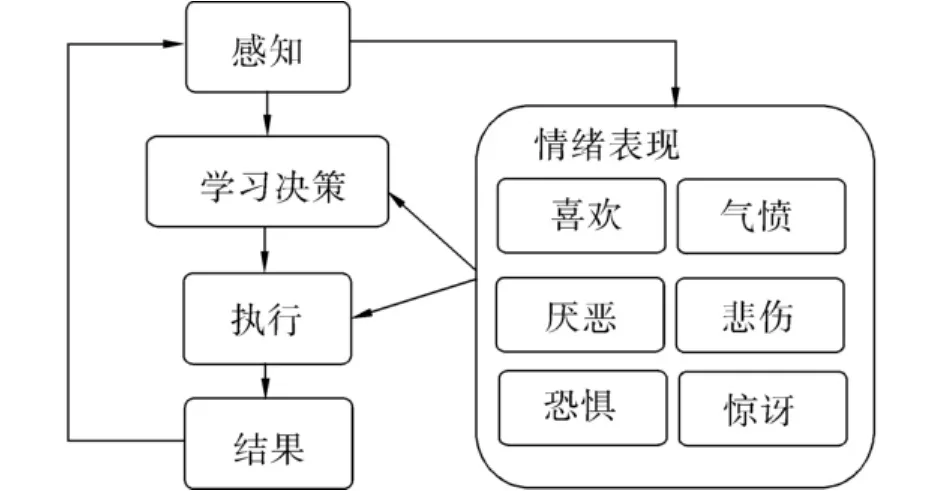
图1 虚拟人的认知结构Fig.1 Cognitive structure of a virtual human

但是在追逐的环境下，被追者的感知只关注追逐者的位置，因此情绪评价只依赖于对追逐者的评价.也就是说，在有限的时空条件下，对事件和对象的评价来不及进行.至于产生何种情绪，也是依赖剧情的.OCC的情绪类型(22种)可以和Ekman的面部表情类型建立映射关系(见表1).Ekman认为人有6种最基本的情绪表现，分别是喜悦、气愤、悲伤、惊讶、厌恶、恐惧，其他的复杂情绪表现都是由这6种基本情绪复合而成的.

表1 OCC情绪类型和Ekman的情绪表现对映关系Table 1 The mapping of OCC emotion type and Ekman’s emotion type

为了方便表示情绪，引入一个情绪集合e={e1，e2，e3，e4，e5，e6}.其中 e1、e2、e3、e4、e5、e6分别表示厌恶、气愤、恐惧、惊讶、悲伤、喜悦这6种基本情绪的表现强度，e表示复合的情绪强度值.同样引入一个刺激集合 si={si1，si2，si3，si4si5，si6}.sij表示刺激强度值.

对于一个行为，不同的情绪源于不同的刺激强

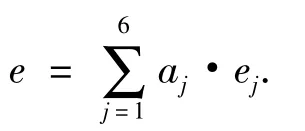
同样，对于同一种情绪表现，刺激虚拟人产生ej情绪的刺激源也可能有多种，假设这些刺激源为s1，s2，…，sn.但是每种刺激源驱使虚拟人产生ej情绪的强度也不同，所以同样要引入权值，假设刺激源si(i=1，2，…，n)刺激虚拟人产生ej情绪的权值为bij，则经过这些事件的刺激后，虚拟人的ej可表达为度.如针对逃跑这个行为，恐惧的情绪更容易使虚拟人做出逃跑的决策.所以要引入权值.以被追者为例，假设被追者的基本情绪值为 ej(j=1，2，…，6)，该情绪促使被追者做出逃跑决策的权值为aj，则被追者在刺激的作用下做出逃跑行为的情绪值为

对于运动中的虚拟人，情绪值越大，表示虚拟人越兴奋，这样更有利于虚拟人的运动.在动物世界的追逐游戏中，追逐者总是希望尽快追到目标，为此，可能采取以下的策略:1)加快追赶速度;2)放慢逃跑的速度使被追者放松警惕.但在现实世界的各种追逐事件中，追逐者必须采取上述混合策略.例如，非洲狮子潜伏猎杀其他动物，开始时悄悄靠近(而不是快速奔跑)，为的是不惊动其他动物(使其情绪值尽可能小).当目标开始警惕时(情绪值上升)，狮子开始加快速度追赶.但归根结底，追逐者和被追者总是希望自己的情绪表现比对手大，这样在追逐中对自己更有利.因此，当对手情绪值小时，自己的情绪也小.

本文的追逐剧情，与上述情况相类似.情绪博弈体现在把情绪因素引入到追逐的过程中，追逐双方总是希望对方的情绪值比自己的低，因为情绪值降低不利于对手快速采取行动，从而有利于自己的收益.

2 追逐过程中的数学模型

2.1 追逐的剧情假设

在一个封闭的院子里发生了一起凶杀案，院子中间有2个竖直放置的圆柱形粮仓，粮仓的半径为R.案发前，受害者为了逃避凶手的伤害，绕着粮仓和凶手进行周旋.凶手也只好绕着粮仓追逐受害者.本文以绕着粮仓追逐的过程为研究对象，将2人分别命名为追逐者(chaser)和被追者(escaper).为了尽量准确地模拟这个追逐过程，需要考虑虚拟人的情绪变化、策略和虚拟人的体力、体质量、速度等因素.各因素之间的关系如图2所示.

图2 追逐过程中各因素间的关系Fig.2 The relationship of the factors concerned

2.2 虚拟人的情绪模型

对于追逐者，驱动追逐者的追逐行为主要是气愤的情绪，暂且忽略其他情绪对逃跑行为的影响.假设在追逐的过程中，追逐双方都可以观察到对方的情绪变化.本文中，使追逐者产生气愤情绪的刺激源有2个:两者之间的距离变远;被追者的情绪表现强度增强.并且这2个刺激源使追逐者产生气愤情绪的刺激强度是不同的.所以追逐者气愤的情绪值可表示为

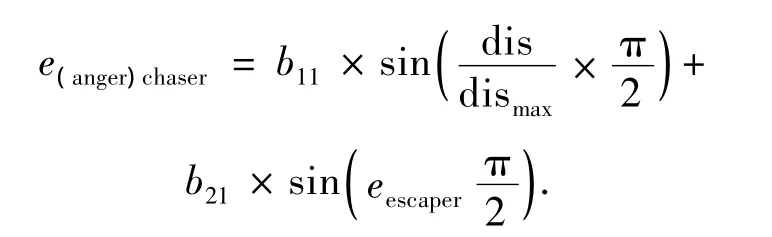
式中:dis表示两者之间的当前距离，dismax表示两者之间的最大距离，eescaper表示被追者的情绪表现强度，b11、b21分别表示2个刺激源促使虚拟人产生气愤情绪的权值.

对于被追者，驱动被追者产生做出逃跑行为的是恐惧和厌恶的情绪.使被追者产生恐惧情绪的刺激事件有3个:两者之间的距离变小;追逐者的情绪表现强度比较强;被追者自身体力的下降.使被追者产生厌恶情绪的刺激事件有2个:追逐者总是紧追不放;追逐者情绪表现强度比较强.被追者恐惧的情绪值可表示为

式中:pescaper表示被追者的当前体力，pescaper(max)表示被追者的最大体力，b12、b22、b32表示3个刺激源促使虚拟人产生恐惧情绪的权值.b12、b22、b32的值由式(1)求出.被追者厌恶的情绪值表示为

式中:b13、b23是2个刺激源促使虚拟人产生厌恶情绪的权值.

所以，刺激被追者做出逃跑事件的情绪值为

2.3 虚拟人的速度模型

为了简单起见，本文将人体比作一个交通工具，设人的最大牵引力为Fmax，人在跑步的时候要克服各种各样的阻力，如重力和摩擦力，并且速度越大，需要克服的阻力越大，消耗的能量也就越多.

根据人体生物力学原理，随着人体的运动，体能逐渐消耗，呼吸变得急促，然后获得更多的氧，体能得到恢复.体能的恢复速度与当前的体力多少有关，体能越少，体能的恢复速度越快，但是人的肺活量和人体的供氧能力有限，所以体能恢复速度也就有限.虚拟人的速度为

式中:v0为初速度，F为虚拟人当前的牵引力，m为虚拟人的体质量，f为虚拟人在当前时刻所受的阻力.虚拟人的牵引力与虚拟人当前的情绪值、体力值和决策值有关，情绪值的强度越强，体力越充沛，F的值越大.模型如下:

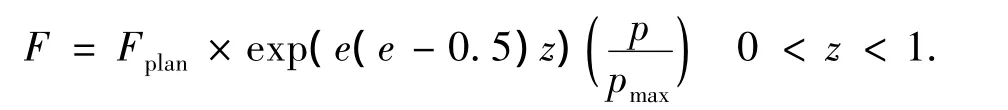
式中:Fplan为虚拟人的计划牵引力，大小与虚拟人所用的策略有关，最大不超过虚拟人的最大牵引力;z为虚拟人的神经质指数，z越大，表示虚拟人越神经质.根据物理学知识，跑步过程中所受的阻力的大小与速度的大小和体质量成正相关，模型为

式中:q1、q2、q3为控制参数.

2.4 虚拟人的体力模型

虚拟人在追逐过程中，体力的消耗速度与虚拟人的速度、加速度和体质量成正相关.体力的变化模型如下:

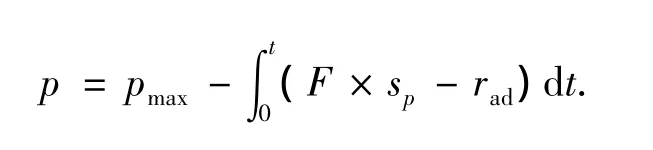
式中:pmax表示虚拟人的最大体力，sp表示虚拟人当前速度的大小，rad表示虚拟人的体力恢复速度.根据人体生物力学原理，人的体力的恢复速度与当前的自身体力值和肺活量的大小有关，肺活量越大，体力值越小，体力的恢复速度就越快，模型如下:

式中:vc表示虚拟人通过呼吸实现的体力恢复速度，u为控制参数.

3 虚拟人情绪博弈的算法

3.1 情绪博弈的过程

博弈的过程必定涉及到策略的选择，所以给追逐者和被追者设定了几个可以供他们选择的策略.追逐者的策略集:{守株待兔，欲擒故纵，声东击西}.被追者的策略集:{走为上计，以逸待劳}.如图3所示.

图3 虚拟人的博弈树Fig.3 Game tree of virtual human

守株待兔:追逐者原地等待被追者自己送上门，当被追者送上门的时候迅速发力.该策略的过程包括2个阶段:1)原地等待被追者的出现;2)当被追者出现的时候，迅速发力，以最快的速度去追被追者.

欲擒故纵:追逐者在进攻前故意放慢速度，以迷惑对方，等待合适的机会迅速出击.该策略的过程包括2个阶段:1)首先悄悄靠近被追者，此时，虚拟人的计划牵引力人为定为Fplan=0.5×Fmax;2)当被追者进入追逐者的攻击范围或者被追者提前行动的时候，迅速发力，以最快的速度追被追者，此时，虚拟人的计划牵引力为Fplan=Fmax.

声东击西:追逐者佯装从一个方向去追被追者，实际上是计划从另一个方向堵截被追者.该策略过程也包括2个阶段:1)佯装去追被追者，迫使被追者迅速逃跑，计划牵引力为Fplan=Fmax;2)当被追者逃出追逐者的视线范围之外的时候，迅速反向从另一侧包抄被追者，计划牵引力为Fplan=Fmax.

走为上计:看到追逐者靠近的时候，马上逃离追逐者，计划牵引力为Fplan=Fmax.

以逸待劳:被追者不先出击，静待追逐者的动静，养精蓄锐，以对付疲惫的追逐者，此时的计划牵引力为0.

假设2个参与者在每次行动之前只能考虑到一步策略，并且2个人并不知道哪个策略是最优策略，只能逐个尝试，如果遇到效果比较好的策略则一直用该策略，否则换其他策略.

3.1 .1 参与者的支付函数

支付函数是参与者从博弈中获得的效用水平，它是所有参与者战略或行动的函数，是每个参与者真正关心的东西.每个参与者都想通过最小的体力消耗得到尽可能好的结果.本文中，根据剧情的设计，追逐者首先采取行动，所以一次博弈所用的时间是追逐者采用一种策略所持续的时间，也就是从这一个策略被开始应用的时刻到该策略结束的时刻.追逐者支付函数为

式中:disstart为一次博弈开始的时候两者之间的距离，disend为这次博弈结束的时候两者之间的距离，p(chaser)start为一次博弈开始的时候追逐者的体力值，p(chaser)end为这次博弈结束的时候追逐者的体力值，m1、m2为控制参数.

被追者支付函数为

支付函数是求参与者利益的函数，此处的利益是指“客观利益”，也就是不带情绪色彩的利益.但是，通常同一个人在不同的时候对同样利益的主观评价是不一样的.所以要引入参与者对事物的主观评价因素.

3.1 .2 参与者对利益的主观评价函数

对一个事物的主观评价是有情绪成分的，根据经验，心情好时候的评价会好于心情坏时候的评价.这个主观评价又会影响到下一步的策略选择.

追逐者的评价函数为

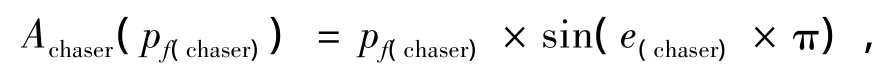
被追者的评价函数

如果评价函数大于一定值则说明参与者对该结果满意，下次还会选择该策略;否则，说明参与者对该结果不满意，下次会选择其他策略.

3.2 博弈过程中虚拟人注意力的分配

由于人的精力有限，所以在追逐过程中，不能在同一时刻对所有的影响因素都高度关注，只能将注意力分散到各个因素中去.以被追者的恐惧情绪为例，如果被追者感觉自己的情绪表现强度较高，并且引起了追逐者的注意，那么b22的值会变大，相应的b12和b32的值会减小.虚拟人注意力分配如下:

1)首先衡量各种情绪的刺激事件，并且给这些刺激事件赋予初始的权值.

2)在追逐过程中根据虚拟人对各种刺激事件投入的注意力的变化来调节权值的大小.调节权值的方法为

重复2)直到追逐者追上被追者或者追逐者体力耗尽为止.

4 实 验

实验中参数的取值如表2所示.

表2 模型中参数的取值Table 2 The value of parameters

a1=0.25，a3=0.75，追逐者的体质量为80 kg，被追者的体质量为95 kg;假设追逐者的最大体力为41 820 J，被追者的最大体力为41 820 J，追逐者和被追者的初始速度都为0.追逐者和被追逐者相应的z值分别为0.33和 0.5，vc为200 J/s.本文设计了 2个实验场景，一个是2个虚拟人绕一个粮仓追逐，另一个是虚拟人绕2个粮仓追逐.当虚拟人绕2个粮仓追逐的时候，追逐者的追逐行为受到气愤和惊奇这2种情绪的影响，假设追逐者惊奇的情绪受被追者速度的影响，表示为

在此情况下，追逐者的情绪强度为

实验中，a2、a4的取值分别为 0.9 和 0.1.实验采用OpenSceneGraph图形库实现了动画虚拟过程的三维仿真，如图4所示，实验结果如图5～12所示.

图4 虚拟人追逐过程的三维仿真Fig.4 The 3-D simulation of chasing behavior

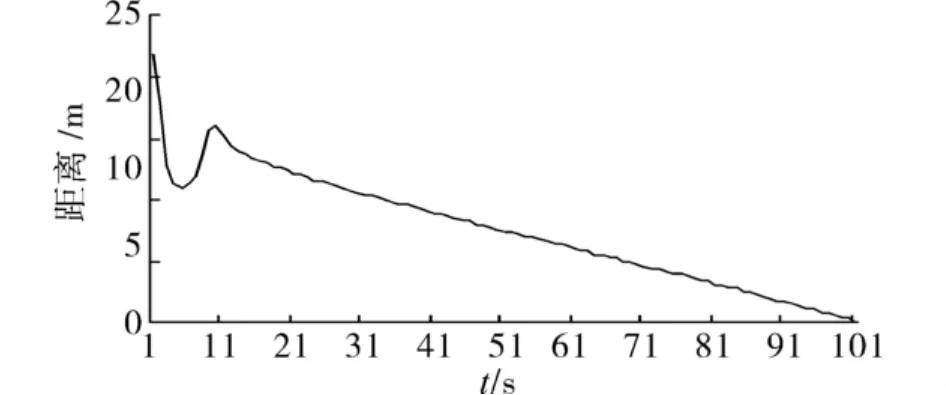
图5 绕1个粮仓追逐时两者之间的距离变化趋势Fig.5 The change of the distance when chasing around a barn

图6 绕1个粮仓追逐时被追者的情绪的变化趋势Fig.6 The change of Escaper＇s emotion when chasing around a barn

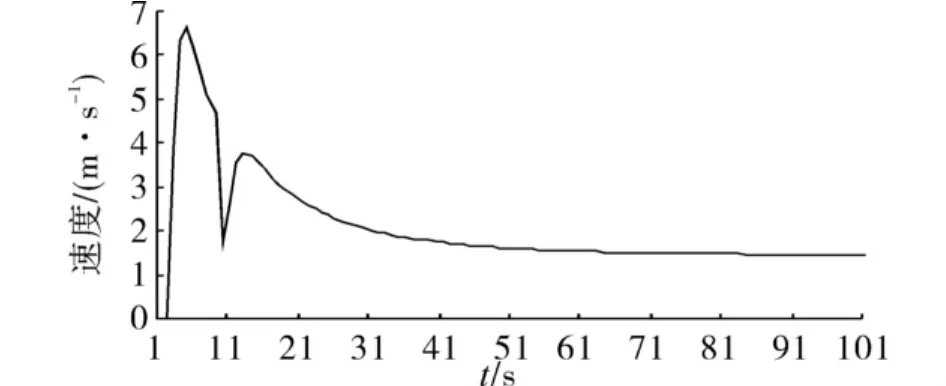
图7 绕1个粮仓追逐时被追者速度的变化趋势Fig.7 The change of escaper’s speed when chasing around a barn

图8 绕1个粮仓追逐时被追者体力的变化趋势Fig.7 The change of escaper’s physical strength when chasing around a barn

图9 绕2个粮仓追逐时两者之间的距离变化趋势Fig.9 The change of the distance when chasing around two barn

图10 绕2个粮仓追逐时被追者的情绪变化趋势Fig.10 The change of Escaper＇s emotion when chasing around two barn

图11 绕2个粮仓追逐时被追者的体力变化趋势Fig.11 The change of escaper’s energy when chasing around two barn

图12 绕2个粮仓追逐时被追者的速度变化趋势Fig.12 The change of escaper’s speed when chasing around two barn

从图5～12可以看出，当被追者感觉到自己的体力下降，并且追逐者距离自己越来越近的时候，被追者的情绪值迅速增加，最终徘徊在一个较高的情绪值;情绪值迅速增加的时候，被追者的速度也迅速增加，但是随着被追者体力的下降，被追者的速度也下降.在绕2个粮仓追逐时，被追逐者的运动方向有变化.这大体上符合人的追逐行为的特点.本实验中追逐者的实验结果与被追者的实验结果类似.

5 结束语

构建人类追逐行为模型是一个令人感兴趣的研究方向，追逐过程很好地体现了个体间的体力和心智的博弈，而情绪是描述追逐过程的一个重要参量.以往对追逐问题的研究多采用运动学方法，缺少有关情绪仿真方面的研究.由于追逐模型在虚拟仿真领域具有广泛的应用价值，因此亟需从智能科学的角度重新审视追逐过程.

本文考虑了追逐过程中人的情绪参数和生理参数，建立了人物追逐过程中的情绪强度计算公式，定量描述了速度和体力变化，并提出了一个情绪博弈的算法.在计算机上进行了仿真实验，实验结果表明:虚拟人在追逐过程所表现出的相互距离、体力和情绪的变化与真实生活的观察经验相符合.

由于时间和水平所限，本文仅考虑了心理参数中的情绪变量，而实际上人的行为参数还有很多，研究结果仍需要进一步深化.下一步的工作拟考虑虚拟人的其他参数(如动机和个性)，采用基于物理引擎的人体动画技术，完善本文的工作.

［1］杨征南.虚拟演兵——兵棋、作战模拟与仿真［M］.北京:解放军出版社，2007:204-207.

［2］蔡红霞，胡小梅，愈涛.虚拟仿真原理与应用［M］.上海:上海大学出版社，2010:28-33.

［3］吴广谋，吕周洋.博弈论基础与应用［M］.南京:东南大学出版社，2009:190-202.

［4］LOOMES G，SUGDEN R.Regret theory:an alternative of rational choice under uncertainty［J］.Economic Journal，1982，92:805-824.

［5］BELL D E.Regret in decision making under uncertainty［J］.Operations Research，1982，30:961-981.

［6］MELLERS B A，SCHWARTZ A，HO K，et al.Elation and disappointment:emotional responses to risky options［J］.Psychological Science，1997，8:423-429.

［7］LOEWENSTEIN G，WEBER E，HSEE C，et al.Risk as feelings［J］.Psychological Bulletin，2001，127(2):267-286.

［8］TU X，TERZOPOULOS D.Artificial fishes:physics，locomotion，perception，behavior［C］//Proceedings of Special Interest Group for Computer Graphics.Orlando，USA，1994:43-50.

［9］FUNGE J，TU X，TERZOPOULOS D.Cognitive modeling:knowledge，reasoning and planning for intelligent pedestrians［C］//Proceedings of Special Interest Group for Computer Graphics.Los Anheles，USA，1999:29-38.

［10］BLUMBERG B，DOWNIE M，IVANOV Y，et al.Integrated learning for interactive synthetic characters［J］.ACM Transactions on Graphics，2002，21(3):417-426.

［11］刘箴，潘志庚.虚拟人动机驱动的自主情绪模型研究［J］.中国图象图形学报，2009，14(5):773-781.

LIU Zhen，PAN Zhigeng.Research on motivation-driven based autonomous emotion model for virtual human［J］.Journal of Image and Graphics，2009，14(5):773-781.

［12］BOURG D M，SEEMANN G.游戏开发中的人工智能［M］.O’Reilly Taiwan公司译.南京:东南大学出版社，2006:14-28.

［13］李力，周昌乐.基于范德波尔方程的情绪模型［J］.厦门大学学报:自然科学版，2011，50(4):703-706.

LI Li，ZHOU Changle.Models of emotions based on van der pol equation［J］.Journal of Xiamen University:Natural Science，2011，50(4):703-706.

［14］涂序彦，韩力群，王洪泊.广义人工生命［M］.北京:科学出版社，2011:43-51.

［15］史忠植.智能科学［M］.北京:清华大学出版社，2006:372-380.

［16］王志良.人工情感［M］.北京:机械工业出版社，2009:60-76.