基于FPGA的全流水双精度浮点矩阵乘法器设计

刘沛华，鲁华祥，龚国良，刘文鹏

(中国科学院半导体研究所神经网络实验室，北京100083)

矩阵乘法是数字信号处理领域中的基本操作，广泛应用于各种电路计算中，例如数字通信领域的DCM变换、快速FFT变换以及图像处理中的3-D变换等都用到了大规模的矩阵乘法运算.由于矩阵乘法计算复杂性较高(通常为O(n3))，其计算性能直接影响到系统的整体性能.然而传统的矩阵乘法多用处理器串行计算来实现，严重制约了计算速度.要提高矩阵乘法的计算性能，可以通过提升工作频率和算法并行度来实现.现场可编程门阵列(field programmable gate array，FPGA)具有强大的计算性能和逻辑分析能力，特别是它具有并发式的硬件结构和出色的浮点计算性能，适合对矩阵乘法进行硬件加速，是当前的研究热点.

目前，采用FPGA实现矩阵乘法计算的研究已经取得一些成果.在定点矩阵乘法方面，Amira等在FPGA上实现了8位定点的矩阵乘法器，但是该设计所需要的带宽与矩阵规模成比例增加，限制了该设计的可扩展性［1］;Jang等设计的矩阵乘法器只需要固定的带宽，但是所需要的存储单元大小与矩阵规模成正比［2］.在浮点矩阵乘法方面，Campell等设计了一个并行结构矩阵乘法器，该设计中的各个计算单元之间不需要通讯，具有可扩展性，但其所需的存储空间随矩阵维数的增加而增大，并且计算效率不高［3］;田翔等设计了一个实时双精度矩阵乘法器，并在FPGA上完成了方案的实现，但是其计算单元的工作频率不高，限制了计算性能的提升［4］.

本文设计并在FPGA上实现了一个计算性能较高、可扩展性良好的并行双精度浮点矩阵乘法器.为提高工作频率，乘法器中的计算单元采用流水线结构，并运用C-slow时序重排技术解决了环路流水线上“数据相关冲突”的问题，提高了计算效率.此外，本设计所需要的带宽和存储单元大小都是固定的，故可扩展性好.

1 矩阵乘法器设计

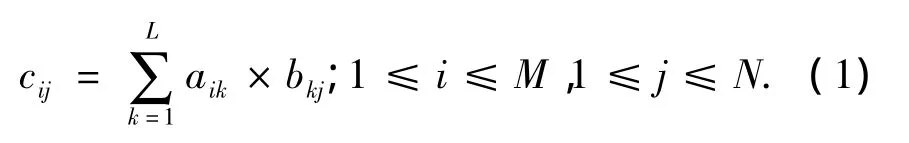
式(1)的计算复杂度为2×M×N×L，即O(n3).为降低算法复杂度，本文设计了一个包含P个处理单元(processing element，PE)的并行双精度浮点矩阵乘法器，其中PE采用流水线结构，并运用C-slow时序重排技术解决环路流水线上“数据相关冲突”的问题，提高了计算效率.设计中所有操作数均为符合IEEE 754标准的64bit双精度浮点数.

1.1 处理单元设计

PE是构成浮点矩阵乘法器的基本单元.每个PE包含一个浮点乘法器、一个浮点加法器和用于存储计算结果的存储单元(Shift register)，其结构如图1所示.

对于矩阵乘法C=A×B，其中A、B和C分别是M×L、L×N和M×N维矩阵，其计算方法如式(1):

图1 PE单元结构Fig.1 Structure of PE

图1中信号分为2类:数据信号和控制信号.其中 a、b、MULTI_RESULT、ADD_RESULT、Q_FB 和output都是64 bit数据信号，其他都是控制信号，具体功能描述见表1.

表1 FPGA内部资源使用情况Table 1 Usage of FPGA internal resources

PE工作时，MULTI_OP_ND置高表示乘法器的输入(a，b)有效，此时启动乘法器，当浮点乘法器计算完毕时，MULTI_RDY输出高电平表示MULTI_RESULT有效;当ADD_OP_ND变为高电平时启动浮点加法器，当浮点加法器计算完毕时，ADD_RDY输出高电平表示乘加过程结束.此外，MULTI_RDY和ADD_RDY还作为Shift register的控制信号，控制Shift register移位.当一组元素计算完毕之后，将输入信号RD_EN置为高电平，读取Shift register中存储的结算结果;当需要计算新的元素时，将NEW_OP置为高电平，Shift register的寄存器全部清零，便可以进行新一轮的乘加运算.

1.2 环路流水线设计

为了提高计算吞吐率，整个PE采用流水线结构.与一般的结构相比，流水线结构能达到更高的时钟频率，但是输出结果与输入之间会有时钟延迟，延迟的时钟周期数等于流水线的级数.流水线的级数(Latency)越高，乘法器与加法器的工作频率就越高.

对于无反馈回路的流水线结构来说，输出结果相对输入之间的延迟不会影响整个系统的顺序执行.但是当流水线结构中存在反馈回路时，若不妥善解决延迟问题，流水线上就会出现“数据相关冲突”.以PE的数据通道为例，图1中加法器端口2的输入数据来自于上一次乘积累加操作的结果，这便构成了一个反馈回路，只有保证MULTI_RESULT到达加法器端口1的时间与上次乘累加的结果(Q_FB)到达端口2的时间一致，才能确保PE的正确运行.否则，必然导致流水线时序紊乱，无法完成给定的计算任务，这就是所谓的“数据相关冲突”.下面通过剖析图2来阐述这个问题.

图2 PE的时序波形Fig.2 Timing diagram of PE

如图2所示，MULTI_RDY比MULTI_OP_ND延迟T1;ADD_RDY比 ADD_OP_ND(即图2中的MULTI_RDY)延迟T2.设CLK的周期为T，浮点乘法器和浮点加法器的Latency值分别为u和v，则T1=uT，T2=vT.设某个计算元素c的前后2组输入数据分别是 a1、b1和 a2、b2.开始计算时 Shift register的寄存器被全部清零，A1=a1b1+0，A1经过一个寄存器延迟得到 Q1;同样，M2=a2b2.由图2可以看出，只有当a2、b2和a1、b1之间保持v+1个时钟周期的延迟时(T2+T=(v+1)T)，才能保证M2和Q1同时到达浮点加法器2个输入端口，进而得到正确的累加结果:A2=Q1+M2.否则，就会导致M2和Q1到达浮点加法器输入端口的时间不一致，发生“数据相关冲突”，无法得到正确的计算结果.

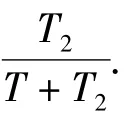
式中:T0为计算的起始时间，d_inA［t］、d_inB［t］分别表示 t时刻 a、b 端口的输入数据，1≤k≤L，0≤s≤v.由式(2)、(3)可知，上述操作的目的是把求解cij，ci+1，j，…，ci+v，j这 v+1 个计算任务交叉编排在一条流水线上执行.同时，上述操作能保证对于cij的计算任务而言，前后2组输入数据保持v+1个时钟周期的延迟，而且不同cij的输入数据不发生重叠.所以，这样一条流水线上能完成v+1计算任务的交叉执行，即一个PE单元花费L(T2+T)时间能完成cij，ci+1，j，…，ci+v，j的 v+1 个元素的求解过程.从而，图 1所示的shift register需要v+1个寄存器来存储计算结果，即n=v+1.

1.3 并行结构矩阵乘法器设计

根据矩阵乘法的简单并行算法，在FPGA芯片上实现P个PE单元，这些PE单元按照图3所示的1×P阵列形式排列.PE单元之间不存在信息交互，它们独立地完成各自的计算任务.由式(2)和(3)可知，每个PE单元进行计算时要用到A的n行和B的某1列数据，整个PE阵列一次计算需要用到A的n行和B的P列数据.将输入矩阵A、B分别按行和按列进行分块:A=［AT1AT2… ATM］T，B=［B1B2…BN］，其中Ai表示A的第i行，Bj表示B的第j列.将A的n行和B的P列作为图3所示系统的输入，图中预处理模块1和预处理模块2的功能分别对Ai和Bj进行处理，使得它们分别满足式(2)和(3)中d_inA［t］、d_inB［t］的要求并将其送入各个 PE单元的a、b端口进行计算.

图3 并行矩阵乘法器结构Fig.3 Timing diagram of PE

通过这种PE的阵列结构，可以完成任意维数的矩阵乘法运算.假设A和B分别为M×L、L×N维矩阵，对于任意的M、N和L值，可以通过下述算法计算C=A×B的结果:

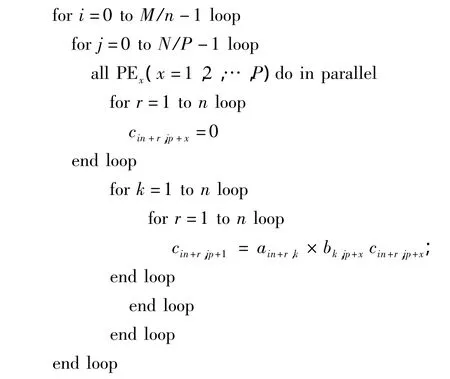
从以上算法可以看出，使用并行矩阵乘法器进行计算时，循环的次数是传统串行算法的1/P，即计算复杂度降低为O(n3/P).同时由于该并行矩阵乘法器中的各个PE单元是相互独立的，因此可以方便地扩展到多片FPGA上实现并行计算.

2 矩阵乘法器性能分析

下面以在FPGA上实现的并行矩阵乘法器来对上述设计的性能进行分析.本文选用Xilinx Virtex-5 LX155芯片实现该设计.PE中的浮点乘法器和浮点加法器使用Xilinx公司提供的floating-point IP核生成.通过对运行速度及该器件中DSP48E单元、CLB单元等资源进行综合考虑，对并行矩阵乘法器进行如下设置:1)IP核生成浮点乘法器时，DSP48E的使用等级设置为Medium Usage(即单个浮点乘法器使用9个DSP48E单元)，Latency的值设定为15;2)IP核生成浮点加法器时，DSP48E的使用等级设置为No Usage，Latency的值设定为9;3)设定矩阵乘法器中PE单元的个数P=10.本设计中所使用的FPGA开发环境和仿真环境分别为Xilinx ISE Design Suite 13.1 和 Mentor Graphics Modelsim SE 6.5a.

2.1 峰值计算性能

理想情况下，每个PE单元在一个时钟周期内可以完成1次双精度浮点乘法操作和1次双精度浮点加法操作，因此整个矩阵乘法器的计算性能可计算为

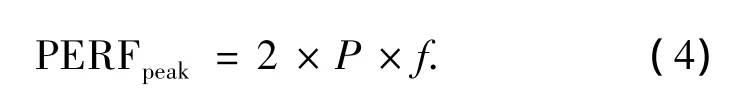
式中:PERFpeak表示矩阵乘法器的峰值计算性能(每秒百万次浮点操作)，P为矩阵乘法器中PE单元的个数，f为矩阵乘法器工作的时钟频率.

FPGA内部资源的使用情况见表2.根据布局布线后仿真的结果，该矩阵乘法器在未做优化的情况下工作频率能达到250 MHz.由此可知该矩阵乘法器的峰值计算性能可达到5 000 MFLOPS.

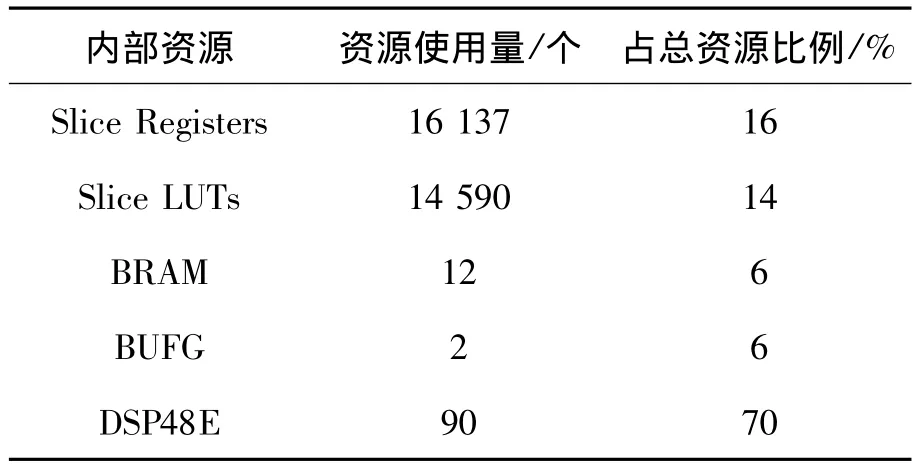
表2 FPGA内部资源使用情况Table 2 Usage of FPGA internal resources

2.2 平均计算性能

并行矩阵乘法器的平均计算性能可以通过计算

2个矩阵相乘所需的总时间来求得，如式(5)所示.

式中:PERF表示并行矩阵乘法器的平均计算性能，F表示2个矩阵相乘总共需要完成的双精度浮点操作次数，t为计算时间.

本文分别以2个128 bit×128 bit的矩阵相乘和2个256 bit×256 bit的矩阵相乘的实例来分析该设计的平均计算性能，如表3所示.

表3 平均计算性能对比Table 3 Comparison of computation performance

由表2、3可以看出，本文设计的并行矩阵乘法器的峰值计算性能可达到5 000 MFLOPS，平均计算性能可以保证在峰值计算性能的85%左右.而田翔等的设计A未采用流水线结构，工作频率只有60 MHz，即使在一片FPGA上集成了25个PE单元，它的峰值计算性能只能达到3 000 MFLOPS［4］.而且，设计A的平均浮点计算性能只能保持在峰值计算性能的50%左右.由此可见，本文设计在计算性能上有大幅度提高.

在矩阵乘法计算中，若FPGA的I/O带宽小于一定值，并行矩阵乘法器中的PE单元就会出现等待状态，此时，带宽便成为制约计算性能的因素.当I/O带宽达到或者高于这个值后，每个PE单元的计算性能则成为制约并行矩阵乘法器计算性能的主要因素.在本文的设计中，PE的计算性能主要由工作频率决定，在工作频率为250 MHz的情况下，只要I/O带宽达到4 GB/s，便不会对整个系统的计算性能产生影响.

3 结束语

本文设计了一个全流水结构的并行双精度浮点矩阵乘法器，并在Xilinx xc5vlx155 FPGA上实现了该方案.矩阵乘法器内部的PE单元采用流水线结构，并运用C-slow时序重排技术解决了环路流水线中“数据相关冲突”的问题，提高了计算效率.实验结果表明，对于不同维数的矩阵乘法，本设计都有较高的计算性能.同时，本文设计的并行矩阵乘法器结构，其内部的各个PE单元相互独立，因而具有很好的可扩展性.在后续的研究工作中，需要提出更为合理的并行结构，通过多片FPGA的并行计算来进一步提高矩阵乘法器的计算性能.

［1］AMIRA A，BENSAALI F.An FPGA based parameterizable system for matrix product implementation［C］//IEEE Workshop on Signal Processing Systems(SPIS’02).San Diego，2002:75-79.

［2］JANG J，CHOI S，PRASANNA V K K.Area and time efficient implementations of matrix multiplication on FPGAs［C］//2002 IEEE International Conference on Field Programmable Technology.Seoul，Korea，2002:93-100.

［3］CAMPBELL S J，KHATRI S P.Resource and delay efficient matrix multiplication using newer FPGA devices［C］//Proceedings of the 16th ACM Great Lakes Symposium on VLSI.Philadelphia，USA，2006:308-311.

［4］田翔，周凡.基于FPGA的实时双精度浮点矩阵乘法器设计［J］.浙江大学学报:工学版，2008，42(9):1611-1615.

TIAN Xiang，ZHOU Fan.Design of field programmable gate array based real-time double precision floating-point matrix multiplier［J］.Journal of Zhejiang University:Engineering Science，2008，42(9):1611-1615.

［5］LEISERSON C，ROSE F，SAXE J.Optimizing synchronous circuitry by retiming［C］//Proceedings of the 3rd Caltech Conference On VLSI.Rockville，Maryland，1983:87-116.

［6］SU Ming，ZHOU Lili.Maximizing the throughput-area efficiency of fully-parallel low-density parity-check decoding with C-slow retiming and asynchronous deep pipelining［C］//The 25th International Conference on Computer Design.Washington，DC，USA，2007:93-100.

［7］肖宇，王建业，张伟.基于IP核的数选式浮点矩阵相乘设计［J］.集成电路应用，2011，37(6):52-55.

XIAO Yu，WANG Jianye，ZHANG Wei.Floating-point matrix multiplication design based on IP core［J］.Application of Integrated Circuits，2011，37(6):52-55.

［8］许芳，席毅，陈虹.基于FPGA Nios-Ⅱ的矩阵运算硬件加速器设计［J］.电子测量与仪器学报，2011，25(4):376-383.

XU Fang，XI Yi，CHEN Hong.Design and implementation of matrix hardware acceleration based on FPGA/Nios-II［J］，Journal of Electronic Measurement and Instrument，2011，25(4):376-383.

［9］黎铁军，李秋亮，徐炜遐.一种128位高性能全流水浮点乘加部件［J］.国防科技大学学报，2010，32(2):56-60.

LI Tiejun，LI Qiuliang，XU Weixia.A high performance pipeline architecture of 128 bit floating-point fused multiply add unit［J］.Journal of National University of Defense Technology，2010，32(2):56-60.