离散时间混合多智能体的拟平均一致性控制

李波，吴淑琴，谷明琴

(1.郑州威科姆科技股份有限公司卫星定位应用工程技术研究中心，河南 郑州 450000;2.中南大学 信息工程学院，湖南长沙 410083)

近年来，多智能体的分布式协调控制如编队控制［1-2］、群集问题［3］、分布式传感器网络［4］、通信网络的拥塞控制［5］等领域受到了极大的关注.Vicsek等提出了一个简单的自驱动的粒子群相变和数值型复杂动力学的模型［6］，Jadbabaie等用图论对Vicsek模型在理论上进行了解释［7］;Olfati-Saber［2］和 Murray［8］介绍了网络动力学一致性问题的理论框架;文献［9］提出了分析多智能体系统的理论框架;Lin等分析了具有变拓扑和耦合时间延迟的多智能体网络平均一致性问题［10］，及二阶多智能体网络的一致性控制问题［11］.与上述方法不同，本文研究了具有混合阶多智能体离散动力学网络的拟平均一致性问题，并提出一致性协议解决该问题.用Lyapunov函数和代数图论分析系统的稳定性，实验结果表明，该方法能够有效解决混合阶多智能体离散动力学网络的拟平均一致性问题.

1 图论和一致性协议

1.1 图论

令G=(V，ε，A)为加权无向图，其n阶顶点集V={v1，v2，…，vn}，边集 ε =V × V，加权邻接矩阵A=(aij)，aij≥0.节点的下标属于有限下标集I={1，2，…，n}，G 的边集记为 eij=(vi，vj).与边相关联的n×n阶邻接矩阵A的元素均为非负，如式(1)所示.

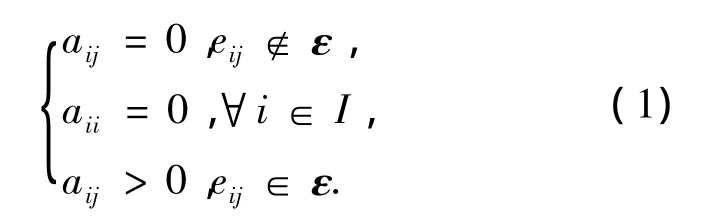
因而，如果图G=(V，ε，A)是无向图或平衡图，那么A就是对称矩阵.

集合 Ni={vj∈V∶(vi，vj)∈ε}表示为 vi的邻集，节点集V的任一子集J称为簇.簇J的邻集定义为

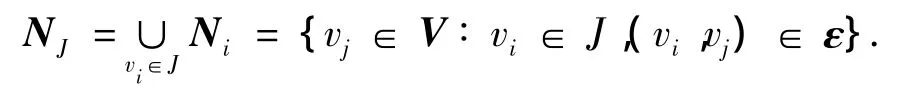
节点vi的入度、出度定义为

对于邻接元素为0-1的图，degout(vi)=|Ni|.图G的度矩阵等于对角阵Δ=［Δij］.

式中:

图G的Laplacian矩阵定义为

由定义知，如果图G是平衡图或无向图，那么Laplacian矩阵的每行元素之和为零.因此，Laplacian矩阵有一个特征值为零，与零特征值所对应的右特征向量为

用Gsw(t)表示变拓扑无向或有向网络，其中切换信号为 sw(t)∶［0，+ ∞)→{1，2，…，M}，M∈Z+.Lsw表示变拓扑网络的Laplacian矩阵.

引理1［8］令 G=(V，ε，A)为加权无向图或有向图，其Laplacian矩阵为L.无向图G节点的最大出度，记为 dmax(G)=maxidegout(vi).那么，L(G)的所有特征值都位于所定义的圆盘内部:

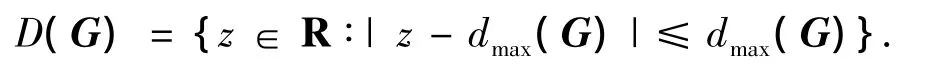
1.2 一致性问题

定义1 令 χ∶Rn→R是n变量的函数 ξ1，ξ2，…，ξn，ξ(0)记为系统的初始状态.动力学网络中的χ-一致性问题是输入ui计算x(ξ(0))的分布式方式，且仅依赖于节点vi自己和它邻近的状态.称状态反馈

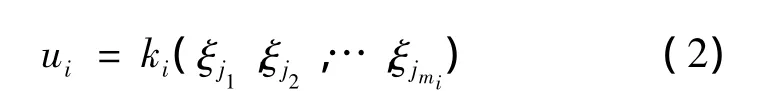
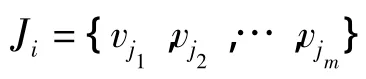
假设多智能体系统是混合一、二阶的异质多智能体系统.智能体的总个数为n，其中一阶和二阶智能体个数分别为n1、n2，每个二阶智能体的动力学方程可以表示为差分方程形式:

式中:ξi(k)=［xi(k)vi(k)］T是二阶智能体的状态，ui(k)是控制输入.矩阵A、B分别为:

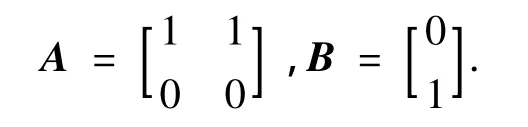
每个一阶智能体的动力学方程可以表示为差分方程形式:

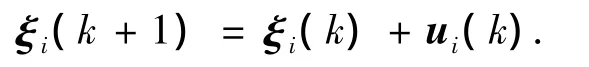
式中:ξi(k)=xi(k).

定义2 离散时间的拟平均一致性问题:假设G=(V，ε，A)是强连通有向网络或连通无向网络.如果存在一个渐近的稳定平衡点ξ*，满足:

提出下面的一致性协议解决混合阶异质积分智能体网络中的一致性问题.

1.3 一致性协议

定义3 对于定拓扑和变拓扑网络，可以用一致性协议来解决拟平均一致性问题:

式中:aij是图的邻接矩阵的元素，步长ζ＞0.

那么式(2)、(3)可以写为统一的形式:

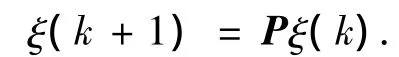
图1是具有4个异质积分智能体的无向网络拓扑结构(其中节点1、3是二阶智能体，而节点2、4是一阶智能体).那么对应于图1的矩阵¯M、˜L、¯L、¯P可以写为:

图1 混合阶智能体的无向网络拓扑结构Fig.1 The topology of network with mixed order integrator agents

相应的系统动力学方程也变为

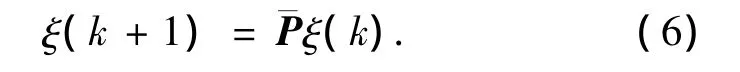
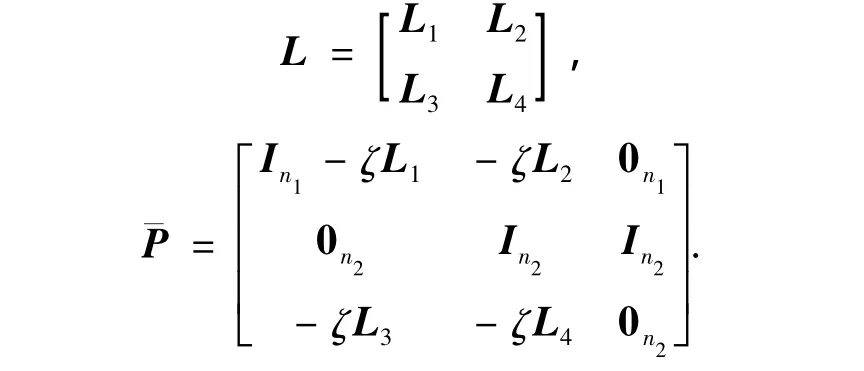
对于离散时间的变拓扑网络结构，系统的动力学方程可以重新写为

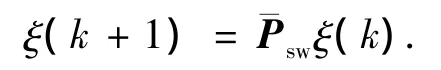
式中:¯Psw表示随着切换信号变化而变化的¯P矩阵.

2 网络动力学的稳定性分析

定理1 如果0＜ζ＜1/(Δmax(G))，则由一阶和二阶多智能体组成的多智能体系统网络是无向连通的或有向平衡连通的，那么¯P的特征值只有一个为1，而其他特征值的模均小于1.且

证明:

从以上推导可以得到下面的矩阵方程:

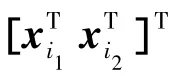
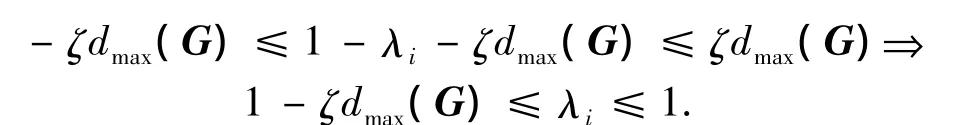
如果要得到|λi|≤1，只需要

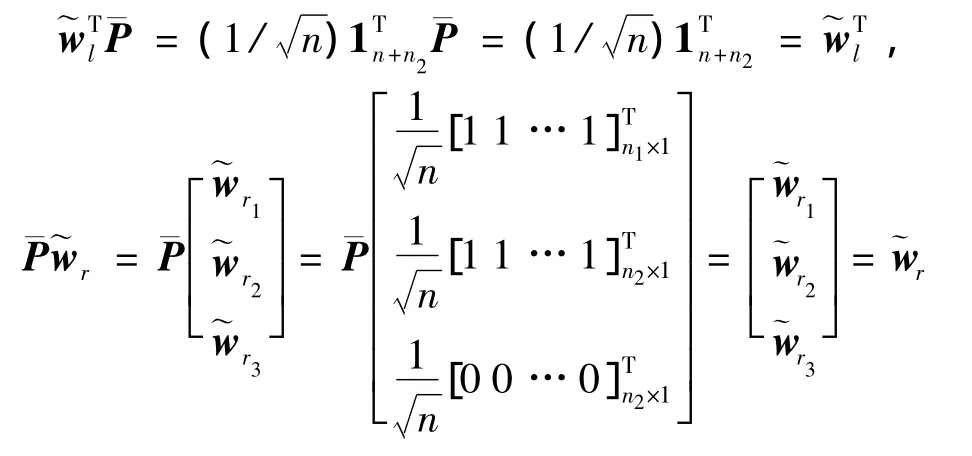
从而可知，1是P¯的特征值.

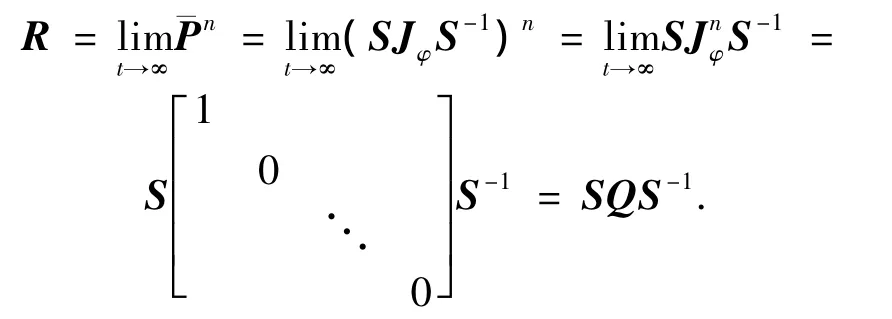
由1)的证明可知，若0＜ζ＜1/(Δmax(G))，则P¯的特征值除一个为1以外，其余特征值的模均小于1.因此，因为JφS=SP¯，可知S的第一列是，因为S－1Jf=S－1，可知S－1的第一行是.由于 SS－1=I，且满足.从而可以得到证毕.

证明

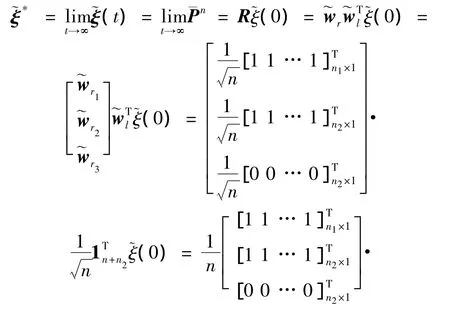
定理3 令Gsw=(V，ε，A)为变拓扑连通加权无向图或强连通平衡有向图，当0＜ζ＜1/dmax(Gsw)(其中dmax(Gsw)表示变拓扑结构中网络节点的最大度)，利用协议(5)可以实现拟平均一致.

证明

由于0＜ζ＜1/dmax(Gsw)，则由定理1可知，系统在k时刻的矩阵除了有一个特征值为1外，其余特征值的模严格小于1.

也成立，因此协议(5)可是实现拟平均一致.证毕.

定义位置的不一致函数:

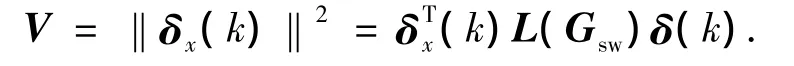
3 仿真结果

图2显示了由6个节点组成的4种不同的无向网络拓扑结构，其中节点1、5为二阶智能体，节点2、3、4、6为一阶智能体，且都具有0～1的权值.这4种网络结构{Ga，Gb，Gc，Gd}都是连通的.图 3 为一个有限状态自动机，状态集为{Ga，Gb，Gc，Gd}.混杂系统从状态Ga开始，每经过一个时间间隔，按照图3所示的状态自动机变化到下一个状态.

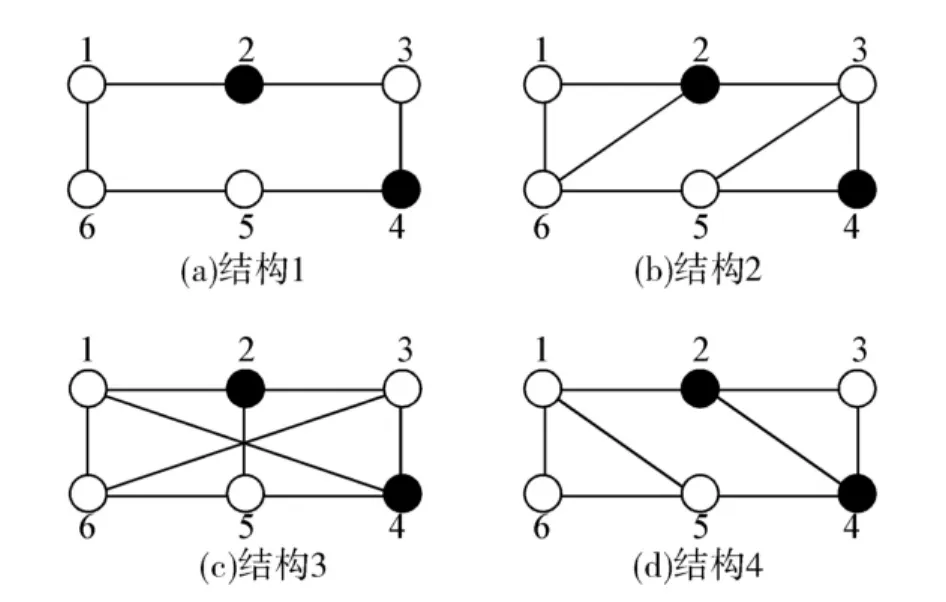
图2 4种拓扑结构Fig.2 4 kinds of topology configurations

图3 4个状态的有限状态自动机Fig.3 A finite automaton with four states

图4～5显示了变拓扑离散时间异质多智能体网络一致性控制的仿真结果.

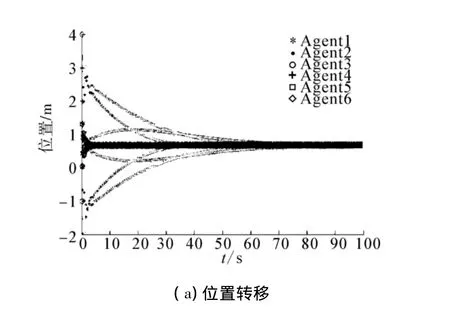
图4 步长为0.33时变拓扑无向网络下的仿真结果Fig.4 Simulation results in switching topology networkwith step 0.33

图5 步长为0.34时变拓扑无向网络下的仿真结果Fig.5 Simulation results in switching topology network with step 0.34

仿真研究中，状态的初值为［3(2，－2)－1(－2，2) － 2 4］T，k=1，一致位置状态分量为0.667，一致速度分量为零.步长分别取不同的值0.33和0.34.从图 5 中可以看出当步长大于 0.33时，系统开始趋于发散.仿真结果证明了稳定性分析的正确性.

4 结束语

本文提出了离散时间多智能体系统上的拟平均一致性问题和协议，分析了一致性协议适用的条件，即如果多智能体系统的网络拓扑结构是连通的且是平衡的，并且步长ζ不大于1/dmax(G)，那么运用提出的一致性协议，可以使系统达到拟平均一致.并在Matlab中仿真了变拓扑无向网络结构的多智能体系统，步长 ζ分别取0.33、0.34，以及相应的位置不一致函数V=‖δx(k)‖2的曲线.仿真结果证明了理论分析的有效性.

［1］FAX A，MURRAY R M.Information flow and cooperative control of vehicle formations［J］.IEEE Transactions on Automatic Control，2004，49(9):1465-1476.

［2］OLFATI-SABER R，MURRAY R M.Distributed cooperative control of multiple vehicle formations using structural potential functions［C］//The 15th IFAC World Congress.Barcelona，Spain，2002:346-352.

［3］REYNOLDS C W.Flocks，herds，and schools:a distributed behavioral model［J］.ACM SIGGRAPH Computer Graphics，1987，21(4):25-34.

［4］CORTES J，BULLO F.Coordination and geometric optimization via distributed dynamical systems［J］.The SIAM Journal on Control and Optimization，2006，44(5):1543-1574.

［5］PAGANINI F，DOYLE J，LOW S.Scalable laws for stable network congestion control［C］//Proc of the Int Conf on Decision and Control.Los Angeles，USA，2001，1:185-190.

［6］VICSEK T，CZIROK A，BEN-JACOB E，et al.Novel type of phase transition in a system of self-driven particles［J］.Physical Review Letters，1995，75(6):1226-1229.

［7］JADBABAIE A，LIN J，MORSE S A.Coordination of groups of mobile agents using nearest neighbor rules［J］.IEEE Transactions on Automatic Control，2003，48(6):988-1001.

［8］OLFATI-SABER R，MURRAY R M.Consensus problems in networks of agents with switching topology and time-delays［J］.IEEE Transactions on Automatic Control，2004，49(9):1520-1533.

［9］OLFATI-SABER R，FAX J A，MURRAY R M.Consensus and cooperation in networked multi-agent systems［J］.Proceedings of IEEE，2007，195(1):215-233.

［10］LIN P，JIA Y M.Average-consensus in networks of multiagents with both switching topology and coupling time-delay［J］.Physica A:Statistical Mechanics and its Applications，2008，348(1):303-313.

［11］LIN P，JIA Y M.Consensus control for networks of agents with double integrator dynamics［EB/OL］.［2010-05-12］.http://www.paper.edu.cn.

［12］LEE D J，SPONG M W.Agreement with non-uniform information delays［C］//Proceedings of the 2006 American Control Conference.Minneapolis，USA，2006:750-756.