最坏情况下Min-2SAT问题的上界

谷文祥，姜蕴晖，周俊萍，殷明浩

(1.东北师范大学计算机科学与信息技术学院，吉林长春 130117;2.长春建筑学院基础教学部，吉林长春 130607)

人工智能研究领域存在着很多计算困难的问题，如 SAT(satisfiability)问题、QBF(quantified boolean formula)问题、智能规划问题、模型诊断问题等.若P≠NP成立，人们将无法为这些问题找到多项式时间的求解算法.这时从理论上分析这些问题在最坏情况下的时间复杂性上界尤为重要，因为此时对该上界的一个微小的改进，例如从O(ck)改进为O((c－ε)k)，就会使得问题求解的算法在效率上获得指数级别的提高.以SAT问题为例，作为第一个被证明是NP完全的问题，改进其在最坏情况下的时间上界受到了研究人员的广泛关注.MaxSAT(maximum satisfiability)问题是SAT问题的扩展，它指的是给定一个命题逻辑公式，找到一组使真值赋值同时满足最多的子句.与SAT问题一样，MaxSAT问题在计算机科学领域有着十分重要的地位，因为它是求解人工智能和组合优化问题的基础［1-2］.当公式中子句的长度至多为2时称之为Max-2SAT(maximum two-satisfiability)问题，它是一个NP完全的问题［3］.近年来，众多学者对Max-2SAT问题进行了研究［4-7］，已经将其最坏情况下的上界缩小到O(2m/6.312)［8］.与 MaxSAT 问 题 相 对 的 是 MinSAT(minimum satisfiability)问题，它指的是给定一个命题逻辑公式，找到一组使真值赋值同时满足最少的子句.虽然人们对MaxSAT问题已经做了非常多的研究，但对MinSAT问题的研究却并不深入.目前，对MinSAT问题的求解主要采用近似方法［9-10］.此外，LI等在文献［11］中将MinSAT问题转换为Max-SAT问题，给出了一个MinSAT求解器.事实上，在求解某些组合优化问题时，将其转化为MinSAT问题比转化为MaxSAT问题有着更快的速度，所以研究MinSAT问题也有着十分重要的理论意义和实际应用价值.正如人们对MaxSAT问题的研究主要集中在Max-2SAT问题上，笔者同样着眼于MinSAT问题中子句长度不超过2的情况，即对Min-2SAT问题进行研究，提出了一种求解Min-2SAT问题的算法，并证明了算法在O(1.134 3m)时间内可解.

1 基础知识

1.1 基本概念

为了讨论方便，首先介绍本文需要的相关概念.

定义1 真值赋值.给定一个布尔变量集合V={x1，x2，…，xn}，定义在V上的真值赋值是一个函数μ:V→{true，false}.每个真值赋值可以用一个n元布尔向量表示.对V中任意一个布尔变量xi，若它在真值赋值μ下取真，则μ(xi)=1，否则μ(xi)=0.

定义2 文字.对任意一个布尔变量x，称符号x和¬x是其文字，其中x是正文字，¬x是负文字.

定义3 纯文字.给定一个公式F和F中任意一个布尔变量x，若x只以正文字或负文字的形式出现在公式F中，则称x为纯文字.

定义4 子句.子句是若干文字的析取，用集合C 表示，C=l1∨l2∨…∨lk，其中 l1，l2，…，lk是文字.子句C中文字的个数称为子句的长度，记作|C|.

k-子句是指子句长度为k的子句.永真子句T指的是对子句的变量任意赋值时子句都是可满足的.

定义5 CNF范式.CNF范式是若干子句的合取，用 F 表示，F=C1∧C2∧…∧Ci，其中 C1，C2，…，Ci是子句.CNF范式F也称为公式，当且仅当每一个子句都可满足时，公式F在赋值μ下可满足.

公式F同时可满足的最少的子句数记为PesVal(F).称文字l出现在子句中如果子句包含l，称变量x出现在子句中如果子句包含x或¬x.本文中，用#(F，l)表示文字l出现在公式F中的次数，用#k(F，l)表示文字l在公式F中的k-子句中出现的次数.

用F［l］表示将F中所有包含l的子句替换为T，消去所有¬l和所有 F中的空子句.用F［l1=l2］表示将所有的l1用l2替代，并将所有的¬l1用¬l2替代.

定义6 Min-2SAT问题.给定一个命题逻辑公式F，找到一组使真值赋值满足最少的子句，如果子句的长度至多为2，则称其为Min-2SAT问题.

定义7 变量的度.变量x的度是指包含x的2-子句的个数，也就是说，如果变量 x的度为 k，则#2(F，x)+#2(F，¬ x)=k.

定义8 变量的邻居.变量x的邻居是指所有和x一起出现在同一个2-子句的变量.

用V(F)表示F中所有变量的集合，对于变量集合V0⊂V(F)，用N(F，V0)来表示变量集合V0的所有邻居.

用G(F)表示一个无向图，V(F)是所有顶点的集合，如果F中2个变量出现在同一个2-子句中，则在这2个顶点之间添加1条边.

1.2 复杂性分析方法

本节介绍分支算法的复杂性分析方法，首先给出分支树的概念［12］.

分支树是由i(i＞0)个结点组成的有限集合Q，其中一个特定的结点为根结点，标记为公式F，除根结点以外的其他结点被划分为j(j≥0)个互不相交的有限集合 Q1，Q2，…，Qj，分别标记为公式 F1，F2，…，Fj.其中每一个集合又都是分支树，称为根结点的子分支树，分别表示对公式F中的某些变量进行赋值后得到的公式，即公式F的子公式.叶子结点标记的公式为空公式或者其中存在一个空子句.

分支树中的每一个结点都有1个分支向量.设分支树中某一个结点是F0，它的子结点分别是F1，F2，…，Fk.则结点 F0的分支向量为 τ =(r1，r2，…，rk)，其中 ri=f(F0)－f(Fi)，f(F0)=m(F0)是公式F0中子句的数目，f(F0)=n(F0)是公式F0中变量的数目.

每个结点的分支向量的值被称为结点的分支数，可用式(1)计算.

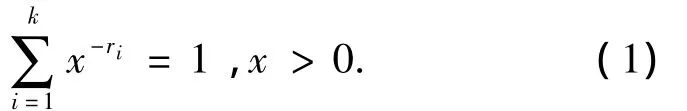
定理1［12］设分支树T的根结点标记为公式F，则分支树T中叶子的个数不超过(τmax)f(F)，其中f(F)是公式F中子句的数目或变量的数目.

由分支树的定义可以看出，分支树的构造过程相当于基于DPLL(Davis-Putnam-Logemann-Loveland)算法的执行过程.算法逐一对公式F中的变量进行赋值，直到确定任意一个赋值满足或不满足公式F为止.假设基于DPLL的算法在分支树T中任意一个结点执行的操作都是多项式的，那么从子句数目的角度考虑，算法的执行时间t为

若从变量数目的角度考虑，算法的执行时间t为

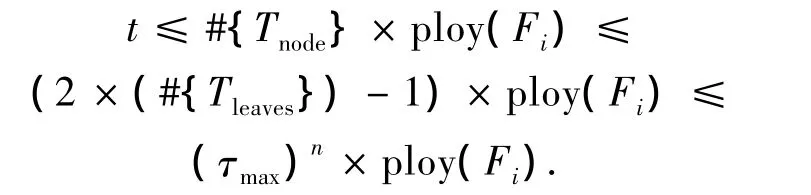
用F表示2-CNF公式，用Ni(F)表示在公式F的2-子句中出现i次的变量的个数.很容易得到

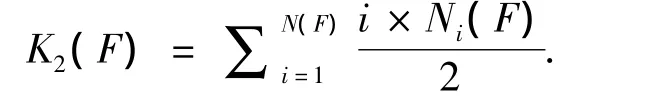
式中:K2(F)表示 F中2-子句的数目.根据文献［13］可以对其稍作修改，得到新的复杂性测度为

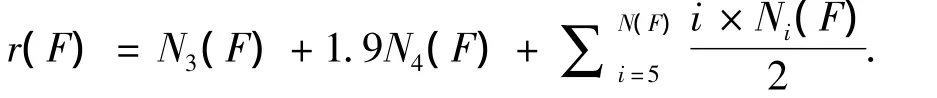
2 化简规则

在给出求解Min-2SAT问题的算法之前，首先给出一个化简算法如下.

化简算法Simplify(F).

输入:一个2-CNF范式F.

输出:一个化简后的2-CNF范式F.

1)如果F=F0∪{C，D}，并且对于一个文字 l有 C{l}=D{¬ l}，则返回 Simplipy(F0∪{C{l}，T}).

2)如果F中存在一个文字l满足#(F，¬l)=0，则返回 Simplipy(F［¬ l］).

3)如果F中存在一个文字l满足#1(F，l)≥#(F，¬ l)，则返回 Simplipy(F［¬ l］).

4)如果F中存在2个变量x1和x2，并且x1至多出现在一个不含x2的2-字句中，令α和β分别为F［x2］和F［¬x2］中通过化简规则对x1所赋的布尔值(true或者false)，则根据α和β的值将公式F化简的方法为:

a)如果 α =false，β =false，则返回 Simplipy(F［¬ x1］).

b)如果 α =false，β=true，则返回 Simplipy(F［x1=¬ x2］).

c)如果 α=true，β=false，则返回 Simplipy(F［x1=x2］).

d)如果 α =true，β =true，则返回 Simplipy(F［x1］).

对于给定的范式，重复使用化简算法Simplify(F)对其进行化简，直到范式不能再应用算法中任何一条化简规则为止.这样在求解Min-2SAT问题时可以减少算法需要考虑的情况，以减弱算法的复杂性.

根据化简规则，可以得到下面的引理.

引理1 令F是一个2-CNF范式，F'=Simplify(F)，则F'中不包含度至多为2的变量.

证明 若变量的度为1，则可通过化简算法Simplify(F)中化简规则2)对其化简;若变量的度为2，则可通过化简规则4)进行化简.因此公式化简后只包含度至少为3的变量.

引理2 令F是化简后的公式，a、x是邻居，a的度为3，则在 F［x］和 F［¬ x］中，至少有一个化简规则会对a赋值.

证明 考虑变量a所有可能出现的情况.

1)当(a∨x)∧(a∨x1)∧(¬ a∨x2)时，若 x=0，则由化简规则3)可知a=1.

2)当(a∨x)∧(¬ a∨x1)∧(¬ a∨x2)时，若x=1，则由化简规则2)可知a=0.

3)当(a∨x)∧(a∨x1)∧(a∨x2)∧¬ a 时，若x=0，则由化简规则1)可知消除了a和¬a，再由化简规则2)可知a=1.

4)当(a∨x)∧(a∨x1)∧(a∨x2)∧¬ a∧¬ a时，若x=1，则由化简规则3)可知a=0.

5)当(a∨x)∧(a∨x1)∧(¬ a∨x2)∧¬ a 时，若x=1，则由化简规则3)可知a=0.

6)当(a∨x)∧(¬ a∨x1)∧(¬ a∨x2)∧a 时，若x=0，则由化简规则3)可知a=1.

由于公式F已化简，所以不存在其他情况，引理得证.

3 算法MinSATAlg

本文给出一个求解Min-2SAT问题的算法Min-SATAlg，它是一个典型的分支算法.具体算法描述如下.

输入:一个2-CNF范式F.

输出:PesVal(F).

1)F=Simplify(F).

2)如果F只包含T字句，则返回L(F).

3)如果F=F1∪F2，并且F1和F2没有相同的变量，则返回MinSATAlg(F1)+MinSATAlg(F2).

4)选择变量 x 使 τ(r(F)－ r(Simplify(F［x］))，r(F)－r(Simplify(F［¬ x］)))最小，并返回min(MinSATAlg(F［x］)，MinSATAlg(F［¬ x］)).

在算法MinSATAlg中，首先，应用化简规则对公式进行化简;第2步是指如果公式中只包含永真子句T，则返回公式中子句的数目;第3步考虑公式中包含组件的情况，即将公式分支成2个更简单的公式并对其递归调用;最后根据每次递归调用返回的结果得到最后的结果.定理1中给出了算法的时间复杂度.

定理2 给定一个2-CNF范式，算法 Min-SATAlg在O(1.134 3m)时间内返回公式中同时可以满足的最少的子句数.

证明

1)当公式F中包含一个度大于6的变量时.由化简规则可知，F中的所有变量至少出现在2个没有x出现的2-子句中.度至少为3的变量使r至少减少1/2，这是因为Ni的2个系数的差至少为1/2.这样，当对x赋值后，r至少减少w(w/2(x被消去)+w/2(x的邻居的度减少)).因此，对x进行分支的复杂度至少为O(τ(6，6)m)=O(1.122 5m).

2)当公式F中变量的度都不超过5时.令x是一个度为5的变量，用kij表示在公式F中出现j次且和x一起出现i次的变量个数，其中1≤i≤j≤5.由于F已化简，所以当j≤2或j－i≤1时kij=0.由于x出现在5个2-子句中，所以有

k13+k14+k15+2k24+2k25+3k35=5.

对于共出现j次并且与x一起出现i次的变量，在对x赋值后其出现在2-子句中的次数为j－i.令F'为对F中的变量x赋值后得到的公式，则有

由此可见，对 x进行分支的复杂度至少为O(τ(5.5，5.5)m)=O(1.134 3m).

3)当公式F中变量的度都不超过4时.与第2种情况类似可得到

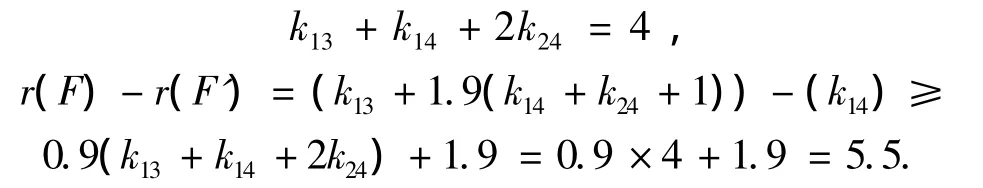
因此，对x进行分支的复杂度至少为O(τ(5.5，5.5)m)=O(1.134 3m).

4)当公式F中所有变量的度均为3时.在这种情况下很容易看出r(F)=N(F)，所以只需要证明以变量数目为参数时的复杂度为O(τ(6，6)n)=O(1.122 5n).由于变量的度均为3，所以变量的个数必为偶数，F的每一次分支都为(2k，2l)，其中k和l都是整数.

a)如果公式F中包含3个变量且其中任意2个变量都出现在同一个2-子句中，则在图G(F)中形成1个三角形.令a、b、c为形成三角形的3个变量，可以看出N({a，b，c})包含至少2个变量，至少1个邻居只和{a，b，c}中的1个一起出现，将其标记为d并和c一起出现，如图1(a)所示.对d进行分支的复杂度为 O(τ(6，6)n)=O(1.122 5n).这是因为对d赋值后，c只和a、b一起出现，或出现在单元子句中，化简规则或者对c直接赋值，或者用包含a、b的子句替代含c的子句.对于前一种情况，a、b也会通过化简规则被消去，对于后一种情况通过化简规则4)会消去a、b中的一个.所以对d赋值后还会至少再消去4个变量，因此对d进行分支的复杂度为O(τ(6，6)n)=O(1.122 5n).

b)考虑图G(F)中不包含三角形的情况.假设F 包含一个变量 x，其邻居为 a、b、c，这样在 F［x］和F［¬ x］中化简规则会对 a、b、c中至少一个赋值.很容易看出对x进行分支的复杂度为O(τ(6，6)n)=O(1.122 5n).

c)下面需要考虑的是对F中的一个变量进行分支时，化简规则会在一个分支中对其全部邻居赋值的情况.考虑一个变量 x，N({x})={a，b，c}.如果|N({a，b，c})|≥5，则 对 x 分 支 的 复 杂 度 为O(τ(4，10)n)⊂O(1.112 0n).如果|N({a，b，c})|＜5，这就意味着或者存在一个变量y≠x并且N(y)={a，b，c}(如图1(b)所示)，或者存在2 个变量y，z≠x并且|N(y)∪{a，b，c}|=2，|N(z)∪{a，b，c}|=2(如图1(c)所示).前一种情况对b分支的复杂度为O(τ(6，6)n)=O(1.122 5n)，后一种情况对x赋值的复杂度为O(τ(4，10)n)⊂O(1.112 0n).

图1 情况4)的不同例子Fig.1 Different cases in 4)

由此可见，以变量数目为参数时的复杂度为O(τ(6，6)n)=O(1.122 5n).从而得到一个化简后的公式F只包含度为3的变量时，则对其中一个变量进行分支的时间复杂度为 O(τ(6，6)m)=O(1.122 5m).

综上所述，给定一个2-CNF范式，算法 Min-SATAlg在O(1.134 3m)时间内返回公式中同时可以满足的最少的子句数，即定理2得证.

4 结束语

MaxSAT问题是求解人工智能和组合优化问题的基础，而在求解某些组合优化问题时，将其转化为MinSAT问题比MaxSAT问题有着更快的速度，因此求解MinSAT问题并分析其复杂度有着很高的实际价值.本文研究了MinSAT问题中每个子句长度不大于2的情况，即Min-2SAT问题，提出了一个求解Min-2SAT问题的算法并证明了算法的时间复杂度为O(1.134 3m)，其中m为公式中子句的数目.笔者运用了一种新的复杂性测度来测量算法的运行时间.另外还证明了对于每个变量至多出现在3个2-子句中的情况，其最坏情况下的时间复杂度为O(1.122 5n)，其中n为变量的数目.

在今后的工作中，可以进一步修正复杂性测度或通过加入冲突子句等方法，来改善算法并减少算法的时间复杂度.

［1］HANSEN P，JAUMARD B.Algorithms for the maximum satisfiability problem［J］.Computing，1990，44(4):279-303.

［2］WALLACE R J.Enhancing maximum satisfiability algorithms with pure literal strategies［C］//Proceedings of the 11th Biennial Conference of the Canadian Society for Computational Studies of Intelligence on Advances in Artificial Intelligence.London，UK:Springer-Verlag，1996:388-401.

［3］NIEDERMEIER R，ROSSMANITH P.New upper bounds for MaxSat［C］//Proceedings of the 26th International Colloquium on Automata，Languages and Programming.London，UK:Springer-Verlag，1999:575-584.

［4］GRAMM J，HIRSCH E A，NIEDERMEIER R，et al.Worst-case upper bounds for MAX-2-SAT with an application to MAX-CUT［J］.Discrete Applied Mathematics，2003，130(2):139-155.

［5］KNEIS J，ROSSMANITH P.A new satisfiability algorithm with applications to Max-Cut:Technical Report AIB2005-08［R］.Aachen，Germany:Department of Computer Science，RWTH Aachen University，2005.

［6］KULIKOV A S，KUTZKOV K.New bounds for MAX-SAT by clause learning［C］//2nd International Symposium on Computer Science in Russia.Ekaterinburg，Russia，2007:194-204.

［7］BINKELE-RAIBLE D，FERNAU H.A new upper bound for Max-2-SAT:a graph-theoretic approach［J］.Journal of Discrete Algorithms，2010，8(4):388-401.

［8］GASPERS S，SORKIN G B.A universally fastest algorithm for Max 2-Sat，Max 2-CSP，and everything in between［J］.Journal of Computer and System Sciences，2012，78(1):305-335.

［9］AVIDOR A，ZWICK U.Approximating MIN 2-SAT and MIN 3-SAT［J］.Theory of Computing Systems，2005，38(3):329-345.

［10］MARATHE M V，RAVI S S.On approximation algorithms for the minimum satisfiability problem［J］.Information Processing Letters，1996，58(1):23-29.

［11］LI Chumin，MANYA F，QUAN Zhe，et al.Exact MinSAT solving［C］//Proceedings of the 13th International Conference on Theory and Applications of Satisfiability Testing.Berlin/Heidelberg， Germany:Springer-Verlag， 2010:363-368.

［12］ZHOU Junping，YIN Minghao，ZHOU Chunguang.New worst-case upper bound for#2-SAT and#3-SAT with the number of clauses as the parameter［C］//Proceedings of the Twenty-Fourth AAAI Conference on Artificial Intelligence.Atlanta，USA，2010.

［13］KOJEVNIKOV A，KULIKOV A S.A new approach to proving upper bounds for MAX-2-SAT［C］//Proceedings of the Seventeenth Annual ACM-SIAM Symposium on Discrete Algorithms.New York，USA:ACM，2006:11-17.