基于协同粒子群算法的PMSM在线参数辨识

，

（华中科技大学 控制科学与工程系，湖北 武汉 430074）

1 引言

永磁同步电动机（PMSM）作为高性能伺服系统的执行元件，为保证其控制性能，需要获得精确的电机参数。而电机参数在实际运行过程中会发生变化，因此有必要对电机参数进行在线辨识。目前电机参数在线辨识方法主要有3大类，分别是基于扩展卡尔曼滤波（EKF）的参数辨识方法，基于神经网络（NN）的参数辨识方法以及基于模型参考自适应（MRAS）的参数辨识方法。但由于3种算法本身的数学理论基础就十分复杂，因此在要求保证算法有效性的基础上，即使尽量简化算法，其形式依旧过于复杂，在实际系统中实现较为困难。同时，3种算法均无法彻底解决多参数同时辨识时的互相耦合问题［1］。文献［2］验证了标准粒子群算法（SPSO）应用于永磁同步电机参数辨识的可行性，但该算法仅对两个相互没有耦合的电机参数定子电阻和负载转矩进行了辨识，没有考虑算法的早熟问题，也没有考虑实际电机运行过程中负载转矩突变时的参数辨识是否准确的问题。

本文提出了一种基于协同粒子群算法（CPSO）的在线参数辨识方法。该算法简单易实现，并且较彻底地解决了标准粒子群算法中的早熟问题和参数辨识中的多参数耦合问题，实现了电机机械参数（包括转动惯量、负载转矩）和电气参数（包括定子电阻、定子电感、转子磁链）的同时在线辨识。

2 PMSM动态数学模型

将永磁同步电动机按转子磁链进行定向，并设Ld＝Lq＝L，则其在两相旋转坐标系（d／q）下的数学模型如下：

式中：id，iq，ud，uq分别为定子电流、电压在d，q轴上的分量；Rs为定子电阻，L为定子电感在d，q轴的分量；np为极对数；ωm为机械角速度；Ψf为转子磁链［3］。

式（1）和式（2）为定子电压方程，式（3）为电机运动方程。本文中要辨识的参数为永磁同步电动机的电气参数Rs，L，Ψf和机械参数J，TL，而式（1）和式（2）中只有电气参数Rs，L，Ψf，式（3）中有电气参数Ψf和机械参数J，TL。这表明电机的电气参数和机械参数可以分开辨识，而将两类参数分开辨识能有效地消除彼此之间的耦合影响所造成的辨识不准问题。则在线辨识中，每一次辨识的基本思路应为：先通过式（1）和式（2）辨识出电气参数Rs，L，Ψf，而后将辨识出的Ψf代入式（3）中，通过该式辨识出机械参数J，TL。

3 协同粒子群算法（CPSO）

粒子群算法本质上是通过粒子追随自己找到的最好解和整个种群的最好解来完成优化。该算法简单易实现，可调参数少。

标准粒子群算法（SPSO）的基本原理如下。

式中：上标k为第k次迭代；c1和c2为非负常数，称加速因子，通常取值在1～2之间；rand1和rand2是在（0，1）区间服从均匀分布的随机数；w为惯性权值，w＝wmax－（wmax－wmin）×step／iteration，step为本次迭代，iteration为总迭代次数［4］。

粒子群算法与其他进化算法（如遗传算法）一样，在寻优过程中都有可能因早熟而陷入局部最优值，以致无法获得实际全局最优。此问题的本质原因是寻优后期粒子群的多样性不足。协同策略是解决这一问题的极为有效的方案。其基本思路是以多个粒子群模块同时寻优，并以一定的频率交换寻优信息，以提高算法的效率。本文在不改变粒子群算法固有的简单易实现优点的基础上，将协同策略引入该算法，提出了一种协同粒子群算法（CPSO），目的是为了在参数辨识过程中，每次均能辨识得到准确的电机参数。

CPSO的基本思路是将整个粒子群划分为M个子种群，让这M个子种群按粒子群算法独立进化，并以一定的通信频率交换彼此有用的信息。该算法内容可描述如下：

Step 1：确定子种群数M，初始化各子种群，并算出每个子种群的gbest和pbest。

Step 2：确定通信频率函数F（t）。

Step 3：令f（t）＝rand（0，1）。若f（t）＜F（t），则选出具有最好的gbest的子种群m，将其他种群的gbest＝gbestm；否则各子种群的gbest均由各子群独立得出。

式(5)中，是θ2，θ3对广义坐标的偏类速度，由式(4)后两式对相应的广义坐标求偏导数，并简化后可求得.

Step 4：根据式（4）和式（5）计算出粒子的新位置，并更新各子种群的gbest和pbest。

Step 5：返回step 3，直至迭代完成。

Step 6：选出各子种群中最好的gbest，即为最终的全局最优解。

在本算法中，通信频率函数F（t）是决定算法性能优劣的一个重要因素。若通信频率过高，则会导致整个粒子群的多样性迅速下降，从而较容易陷入局部最优；若通信频率过低，则会使各子种群的合作优势不明显。本文设定F（t）＝step／iteration。该设定使F（t）在0～1之间线性增加，保证了算法有着合适的通信频率［5］。

4 基于CPSO的PMSM在线参数辨识

对于一个已知对象模型而不知道准确的模型参数的系统而言，参数辨识过程可以看作是一个寻优过程。其基本思路是将对象实际输出与模型输出作比较，二者之间的差距通过一种以适应度函数作为评估标准的寻优算法来缩小，直至差距达到可接受的范围，此时的模型参数值即为所辨识出的参数值［2］。在本文中，该寻优算法为协同粒子群算法（CPSO）。在线辨识过程中，协同粒子群算法（CPSO）对参数的每一次辨识的过程如图1所示。

图1 参数辨识基本框图Fig.1 System frame of parameter identification

本文将电气参数和机械参数分开辨识，根据图1可知，在线辨识过程中每次参数辨识基本步骤如下。

Step 1：获取参数辨识所需的系统输入数据。每组数据包括输入电流和电压id，iq，ud，uq以及机械角速度ωm，这5个量均为实际可测得的值，从而确保了算法在实际中切实可实现。为保证辨识的准确性，必须采样到足够多的系统输入数据，本文设定为采样2 000组数据。采样方式为运行Simulink中的永磁同步电机控制系统模型，2 000组数据采样完成即暂停仿真模型。

Step 2：辨识所需的系统输入数据采样完成后，开始执行电机参数辨识算法。此算法在m文件中实现。首先辨识电气参数，以电机待辨识电气参数Rs，L，Ψf变化可能出现的最大范围作为协同粒子群算法的求解空间，确定CPSO的子种群数、粒子数、迭代次数和通信频率函数F（t），并对所有子种群进行初始化。初始化后各子种群的每一个粒子均为三维，即xi＝［Rs＿i，Li，Ψf＿i］，其中，除一个粒子外，每个粒子的Rs＿i，Li，Ψf＿i为对应电气参数Rs，L，Ψf在求解空间中服从均匀分布的随机值。

Step 3：将各子种群中的每一个粒子（即一组待辨识电气参数的可能解）代入式（1）和式（2）中，选择一种常微分方程求解的方法，根据2 000组系统输入，对已代入一个粒子（即一组电气参数）的电机模型（包括式（1）和式（2））进行求解，计算出2 000组在各采样时刻的电机模型输出然后根据电机电气参数的适应度函数为

N＝2 000时计算出每一个粒子的适应度值，选出每个子种群中适应度值最小的粒子位置作为初始化时各子种群的全局最优解gbest，每一个粒子的位置均为各自粒子的个体最优解pbest。

Step 4：令f（t）＝rand（0，1），F（t）＝step／iteration。若f（t）＜F（t），则选出具有最好的gbest的子种群m，将其他种群的gbest＝gbestm；否则各子种群的gbest均由各子群独立得出。根据式（4）、式（5）更新各子种群的各个粒子。

Step 5：返回Step 3，直至某次迭代的gbest的适应度值小于设定的阀值（即辨识出的电气参数达到精度要求）或迭代完成。

Step 6：选出各子种群中最好的gbest，即为最终的全局最优解。此时的gbest的3个数据即为所辨识出的电机电气参数Rs，L，Ψf。

Step 7：将辨识出的转子磁链Ψf代入式（3），根据该式辨识机械参数J，TL。辨识过程和Step 2－Step 6的过程基本相同，不同之处在于适应度函数和每个粒子的维数。辨识机械参数的适应度函数由于需要辨识的机械参数为2个，则每个粒子为二维，分别代表J和TL。将J和TL辨识出后，所需要辨识的5个参数全部辨识出，一次辨识过程完成。

在本次参数辨识的粒子初始化时，有一个粒子并没有服从寻优空间的随机分布。事实上，该粒子的初值是上次辨识出的电机参数。在辨识电气参数时，初值为上次辨识出的3个电气参数的值；在辨识机械参数时，初值为上次辨识出的两个机械参数的值。这样做有2个原因。

1）这样做能保证机械参数在线辨识的准确性。由式（3）可知，在电机稳定运行的时候，dωm／dt＝0，J为任意值均可满足该式，此时无法通过式（3）辨识出转动惯量J。由于电机处于稳态运行时J和TL不变，则上述做法能保证将电机动态运行时辨识出来的准确的机械参数传递到稳态运行时的参数辨识中，保证了稳态运行时在线辨识的准确性。

2）在连续两次辨识之间的电机参数变化不大的情况下，这样做能使CPSO较迅速地搜寻到符合辨识要求的一组电机参数，极大地缩短了本次辨识所需的时间。这一点在辨识电气参数时体现得尤其明显。

5 仿真及结果

基于Matlab对上述算法进行了仿真研究。本仿真所选取的永磁同步电动机参数标称值为：电机极对数np＝2，定子电阻Rs＝2.875 8Ω，定子电感Ld＝Lq＝8.5mH，转子磁链Ψf＝0.175 Wb，转动惯量J＝0.8e－3kg·m2，摩擦系数B为1.349e－5N·m·s。

在仿真中，设定辨识电气参数和机械参数时算法中各参数均相同。子种群数为6，每个子种群的粒子数为10，迭代次数为40，参数c1和c2均设为1，w由1线性递减至0.4。

所得辨识结果如图2～图6所示。

图2 定子电阻Rs的在线辨识结果Fig.2 Online identification result of stator resistor Rs

图3 定子电感L的在线辨识结果Fig.3 Online identification reslut of stator inductance L

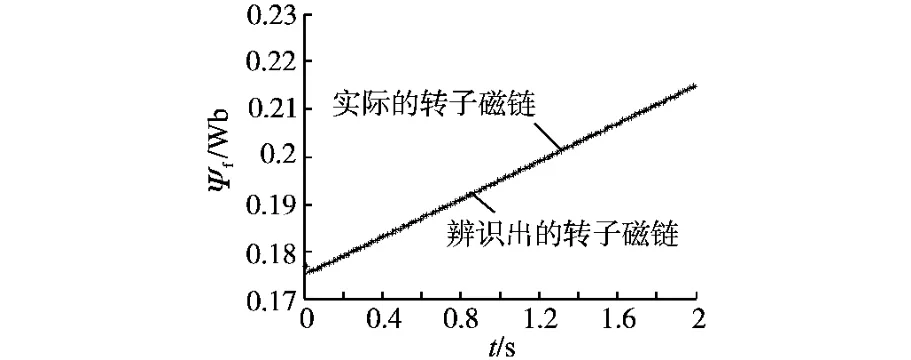
图4 转子磁链Ψf的在线辨识结果Fig.4 Online identification result of rotor flux linkageΨf

从图2、图3和图4可以看出，CPSO对缓慢变化的电气参数的辨识非常有效，能准确地辨识出永磁同步电动机的电气参数。从图5和图6可以看出，该算法能辨识出剧烈变化的机械参数，并且辨识出的机械参数能很快地收敛到实际给定值。由此可见，算法的有效性得到了很好的验证。

图5 转动惯量J的在线辨识结果Fig.5 Online identification result of rotational inertia J

图6 负载转矩TL的在线辨识结果Fig.6 Online identification result of load torque TL

6 结论

本文采用协同粒子群算法准确地在线辨识出了相互耦合的永磁同步电动机电气参数和机械参数，仿真结果验证了算法的有效性。

在设计永磁同步电动机伺服驱动器的速度环和电流环的自整定PI控制器时，需要用到精确的电机电气参数Rs，L，Ψf和机械参数J，TL。本文有效地实现了这5个参数的在线辨识，为伺服驱动器的自整定控制器的设计打下了良好的基础。

［1］张侨.永磁同步电机参数辨识的研究［D］.武汉：华中科技大学，2010.

［2］Liu Li，David A Cartes，Liu Wenxin.Particle Swarm Optimization Based Parameter Identification Applied to PMSM［C］∥Proceedings of the 2007American Control Conference，2007：2955－2960.

［3］李华德.交流调速控制系统［M］.北京：电子工业出版社，2003.

［4］Shi Y，Eberhart R C.A Modified Particle Swarm Optimizer［C］∥Proceedings of IEEE International Conference on Evolutionary Computation，1998：69－73.

［5］周頔，孙俊，须文波.具有量子行为的协同粒子群优化算法［J］.控制与决策，2011，26（4）：582－586.