高职“线性代数”教学内容的探讨

陈 琳，董 艳

(成都电子机械高等专科学校 信息与计算科学系，成都 610031)

高职“线性代数”教学内容的探讨

陈 琳，董 艳

(成都电子机械高等专科学校 信息与计算科学系，成都 610031)

针对当前高职院校“线性代数”课程的教学特点，秉持“以应用为目的，以理论为实际服务”的原则，结合教学中出现的问题，提出以矩阵为基本概念，以矩阵初等变换为主要工具，以求解线性方程组为主线的课程体系，强调在教学内容中注重思想方法和应用。

线性代数;高职院校;教学方法

线性代数是研究矩阵和向量空间的一个数学分支，也是高职院校机、电、信息、经济、管理等专业的一门重要基础课程和工具课程。随着计算机的飞速发展，其解决问题的思想和方法已渗透到各个领域，尤其是计算机、通讯、电子等学科领域，它的重要性和实用性日渐凸显。本文结合高职院校“线性代数”的课程特点及自身的教学实践，对“线性代数”教学内容进行了新的整合，目的是让学生领悟其思想方法，并在抽象的理论教学中体现其实用性，贯彻“以应用为目的，以理论为实际服务”的教学要求，从而达到良好的教学效果。

1 “线性代数”教学内容现状分析

目前，高职院校的“线性代数”课程课时少，任务重，学生数学基础参差不齐。传统教材大多忽略概念、原理和模型的实际意义，教学内容多重理论，轻应用，重公式推导，轻数值计算。学生往往在学完该课程后，只会套用解题，不知道线性代数的应用领域以及如何应用。学生学习目的不明确，为应付考试而学习，这不利于激发学生学习兴趣，不利于培养学生创新能力和实践能力。具体体现在以下3个方面。

1)内容过分追求逻辑的严密性和理论体系的完整性，重理论轻应用，剥离了概念、原理和案例的背景与现实意义，导致教学内容过于抽象，不利于与学生所学的其它课程和所属专业的衔接，造成学生“学不会，用不了”的尴尬局面。

2)传统“线性代数”内容繁多，大体包括:行列式，矩阵及其运算，矩阵的初等变换与线性方程组，向量组的线性相关性，相似矩阵及二次型，线性空间与线性变换。内容繁多而无序，加上难点、重点处理不当，过分突出行列式的内容，而对初等变换重视不够，造成学生思路不清，头绪混乱。

3)传统体系的教材，在教学中，对于行列式的计算与证明，矩阵的基本运算及向量组的线性相关性等内容花费很长的教学时间进行特别细致的讲授，缺少实际应用例题。

“线性代数”教学内容上存在的这些问题直接影响了教学质量，影响了学生对这门课程的学习和掌握，也影响了学生对专业课(如电学、力学等)的学习。

2 “线性代数”教学内容改革

“线性代数”主要处理线性关系的问题。随着数学的发展，其含义也在不断扩大。线性代数的理论不仅渗透到数学的许多分支中，而且在理论物理、理论化学、工程技术、国民经济、生物技术、航天、航海等领域中都有广泛的应用。同时，该课程对于培养学生的逻辑推理和抽象思维能力，空间直观和想象能力具有重要的作用。笔者打破传统“线性代数”教学内容的束缚，突破以往“线性代数”教材的模式，强化数学素质的培养，遵循高职院校“联系实际，深化概念，注重应用，重视创新，提高素质”的教学特点，对教学内容进行了改革。

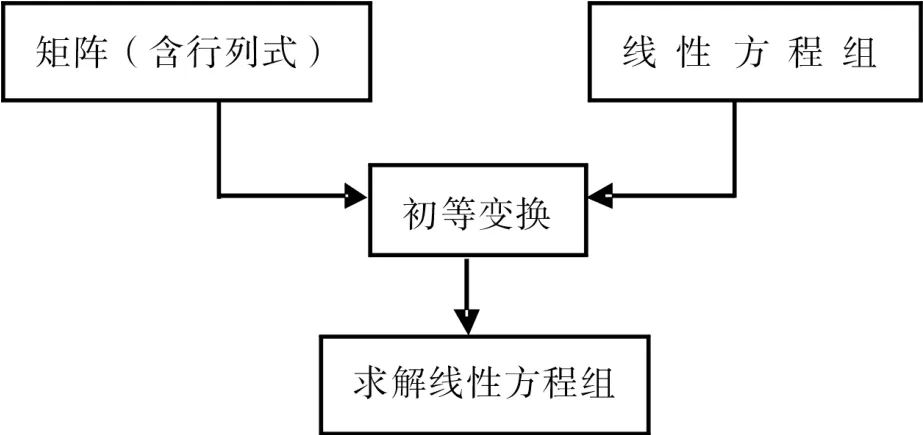
图1 整合后的“线性代数”教学内容

首先对教学内容进行了整合。改变了以往的教学内容和体系，使教学内容合理、有效，教师易于教学，学生易于学习。针对高职院校的特点，将线性代数内容整合为矩阵(含行列式)、线性方程组2个部分。以求解线性方程组为主线贯通线性代数的整个教学过程。突出矩阵的地位，以矩阵为主要知识内容，以矩阵的初等变换为主要计算工具，合理组织矩阵、向量和线性方程组3个部分的内容(如图1所示)。整合后的教学内容充分体现了以下特点:

1)从传统内容到整合内容，教学内容更系统化。鉴于高职院校的教育特点，以求解线性方程组为主线贯通“线性代数”的教学过程;以矩阵为主要知识内容，以矩阵的初等变换为主要计算工具;将行列式作为计算矩阵的工具;尽量只提“列向量，行变换”;在“矩阵的初等变换及应用”中，避开了理论性较强的“初等方阵”，利用矩阵的乘法求逆矩阵。

2)从提出问题到基本概念，教学内容更形象化。要讲清过于抽象的概念是“线性代数”教学的主要难点。教师从实际问题出发，从直观意义或直观解释入手，而不直接从定义出发来组织和展开本课程的教学内容和体系，把抽象的问题通过深入浅出的具体描述，帮助学生理解抽象概念的应用背景，从应用的角度，培养学生学习的兴趣，从而应用于实际。例如，在讲行列式定义时，不是直接从定义入手，而是以高斯消元法求解二元线性方程组为例来引进二阶行列式的定义，并明确地告诉学生行列式只不过是一个为简化书写而用的记号，由此再给出三阶及n阶行列式的定义。在这种氛围中，n阶行列式的抽象性就淡化了。

3)从理论讲授到数学实验，繁琐计算更简约化。每一章节加入了相关实验内容，积极开展数学实验教学，把理论讲授与实践教学有机结合起来。给学生提供综合型、设计型或研究型实验，提高学生数学建模能力和使用数学软件的能力。当基本思想与基本运算掌握后，可以借助Matlab、Mathematica等数学软件来进行各种求解运算，如计算行列式、矩阵运算、矩阵和向量组的秩以及求解线性方程组等等。使学生减少大量计算，把主要精力用于思考解决问题的方法上，从而更高效、更主动地学好“线性代数”。同时，可以加强学生运用计算机及数学软件包的能力，培养其用计算机解决问题的兴趣、能力，调动学生学习的积极性，进一步强化双向翻译能力。

4)从理论教学到实际应用，教学内容更实用化。由于线性代数的理论性较强，学生对线性代数没有感性认识，只会做习题，却不知在现实中如何应用，其实线性代数的应用范围非常广泛，如:城市规划者和交通工程师监控城市道路网格内的交通流量;电气工程师计算电路中流经的电流;经济学家分析产品通过批发商和零售商网络从生产者到消费者的分配，大多数网络问题中的方程组都包含了数百甚至上千个变量和方程。因此教学内容应更加注重理论联系实际，加强应用案例介绍，对传统内容的应用性问题进行更新和充实，增加某些工程问题以外的数学应用题，建立案例库，以利于培养学生应用能力，提高学生的学习兴趣。

5)从理论数学到相应专业，教学内容更专业化。“线性代数”是一门基础课，学习目的就是将学到的理论应用于专业课的学习，服务于专业，如:电学、力学、运筹学等。由于现有的教材在应用型问题方面介绍较少，因此，笔者在讲授线性代数的实际应用背景时，结合实际情况，根据学生所学专业，选用不同的应用案例，使每个学习“线性代数”的学生可以在课堂上了解书本上没有的知识;了解线性代数在自己所学专业的应用，以激发学生学习兴趣，提高教学质量。

3 结语

“线性代数”作为一门基础课程，是学生学好相关专业课的理论基础。“线性代数”课程的教学改革涉及到方方面面，在此仅就教学内容的改革进行了探讨，力求将关于教学内容研究的结果与课堂教学结合起来。关于“线性代数”的教学研究还需要深入的探索。

［1］LAY D C.Linear Algebra and Its Applications［M］.3 版.北京:电子工业出版社，2004.

［2］张国勇.线性代数课程教学内容改革的实践与认识［J］.福建师范大学福清分校学报，2007(5):15-18.

［3］周玲.“线性代数”课程教学点滴谈［J］.大学数学，2005(4):30-32.

［4］吴笑雪.浅谈高职线性代数教育模式探究［J］.数学学习与研究，2009(8):20-21.

［5］李花妮.线性代数教学应重视学生的能力和素质培养［J］.科技信息，2010(3):14，22.

Teaching and Research of Linear Algebra in Higher Vocational Colleges

CHEN Lin and DONG Yan
(Department of Information and Computation Science，Chengdu Electromechanical College，Chengdu 610031，China)

“Linear Algebra”is an important foundation course of various majors in higher vocational colleges.In this paper，the status of teaching contents of“Linear Algebra”is briefly reviewed.The reform of contents and the improvement of teaching method of the course are discussed in detail.The emphasis in the course teaching is concentrated on the introduction of concepts and content recombination on the base of matrix as the fundmentional concept.

Linear algebra;higher vocational college;teaching method

G712.3

A

1008-5440(2012)01-0075-03

2011-03-25

陈琳(1965-)，女(汉族)，四川成都人，副教授，本科，研究方向:应用数学。

董艳(1971-)，女(汉族)，四川成都人，副教授，硕士，研究方向:应用数学。