船用堆堆芯控制棒分布对围板/反射层不连续因子的影响分析

滕辰 蔡琦 陈玉清

（海军工程大学船舶与动力学院，武汉 430033）

0 引言

船用堆存在非均匀性，引入等效均匀化理论[1]计算包含不连续因子在内的组件均匀化参数后，反应堆静态物理特性的模拟精度得到显著提高。但是船用反应堆控制棒大距离移动积分价值的计算上仍存在明显的误差，堆芯外围的四组、五组控制棒问题尤为突出。通过分析，发现仅仅利用一维模型对船用堆围板/反射层节块进行均匀化处理过于简单。虽然可以满足船用堆静态物理特性的仿真精度，但无法反映堆芯控制棒棒态发生变化时引发的不对称性对围板/反射层均匀化参数尤其是不连续因子的影响。参考文献[2]中的二维围板/反射层计算方法，结合 TPFAP中的穿透概率模块编写了围板/反射层等效均匀化参数计算模块TPBWRHP并通过了ZION算例的验证。利用该模块对不同棒态下围板/反射层节块进行了计算分析，并结合非线性迭代半解析节块方法[4]程序对全堆进行扩散计算。计算结果表明，考虑堆内控制棒状分布态变化对围板/反射层节块的影响，能够有效跟踪控制棒价值随棒位的变化特性。

1 等效均匀化理论介绍

传统均匀化方法假定组件的界面净中子流为零并把注意力集中到单个节块的反应率守恒上，忽略了均匀化区域净中子流的守恒。这一假定对于大型电站堆芯的组件计算来说能较好的吻合，但对于小型船用压水堆来说，由于它存在较大的非均匀性，会给组件计算带来较大的误差。

等效均匀化方法则首先是保证区域交界面上的中子流守恒。但是，这也导致了区域交界面上均匀化后的中子通量不连续，因此需要引入不连续因子来保证区域交界面上的非均匀中子通量连续。非均匀中子通量连续关系可用下式表示：

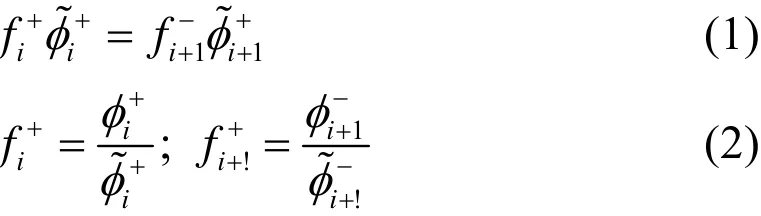
2 围板/反射层等效均匀化参数的计算

通过修改TPFAP中的穿透概率模块使之能对组件进行非对称计算，并利用它对全堆芯进行输运计算，求出围板/反射层节块的非均匀中子通量分布以及面中子通量和净中子流分布，然后利用边界净中子流为零的条件求解围板/反射层节块的二维扩散方程获取节块面通量的均匀解，最后利用式(2)计算不连续因子。

对每个均匀化围板/反射层节块，考虑均匀化区域[5]，{（x,y）:-h1/2≤x≤h1/2; -h2/2≤y≤h2/2},h1为节块的宽度，h2为节块的长度，如图1所示。建立无源节块两群扩散方程为[6]：

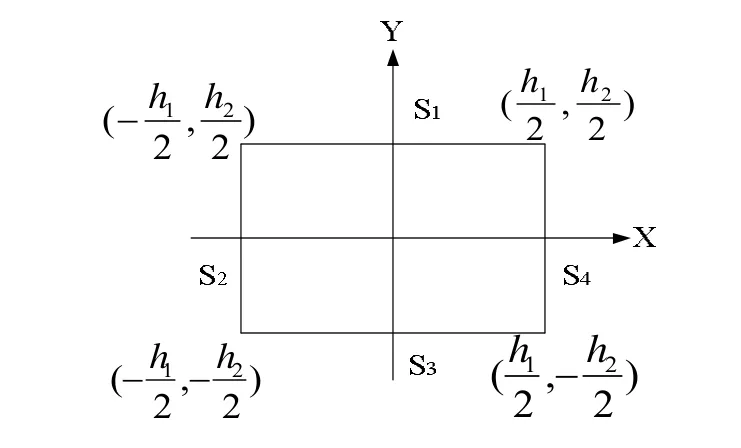
图1 节块坐标示意图

经过两维非均匀输运计算，可以得到围板/反射层区域内中子通量及面平均中子通量和面平均中子流的非均匀输运解的具体分布。因此，可以用非均匀中子流作为节块的边界条件,具体分布可参见图2。文献[5]求解系数过程中的方程组达到八阶，太过复杂。可以将方程化为四个二阶方程进行解析求解，更有利于程序编写。

观察上述方程可以发现，系数a1，b1所在的等式与a2，b2所在等式是不相关的。因此可以对两个二阶方程进行求解。又因sinh(x)为奇函数, cosh(x)为偶函数的特点可将上述方程进一步简化：

所以容易求得系数：

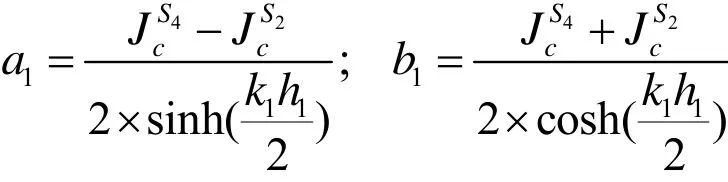
求出方程系数后，求取节块均匀化后表面的平均中子通量。沿节块的每个表面对中子通量做积分[5]：

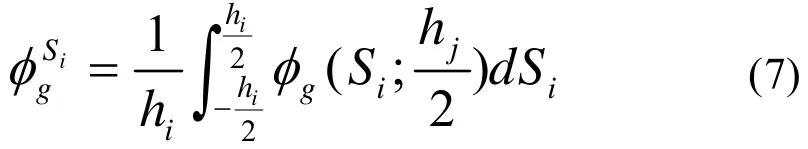
其中，si为积分面；hi为该面的长度；hi/2为该面的不变坐标值；g=1,2。由不连续因子的定义，可以得到每个节块每个面上的不连续因子是：

其中，‘het’和‘hom’分别表示非均匀化的结果和均匀化的结果。

3 船用堆芯外层组件与反射层的非均匀性分析

3.1 堆芯外层组件非均匀性分析

船用反应堆组件横截面呈方形，由圆柱形燃料栅元紧密排列而成，内部对称布置有多个孔道，其中可以是水洞、可燃毒物棒、控制棒等。水洞对中子的慢化效果十分明显，可燃毒物棒和控制棒均具有大的吸收截面，控制棒的棒位变化在组件中形成了强吸收区域和水洞区域等都是造成反应堆非均匀性的主要原因。船用反应堆体积小，中子通量难以展平也是造成反应堆非均匀的另一个重要原因。图3、4分别为利用TPFAP计算的含有多束控制棒的组件 M 和多个水洞的组件 N的热中子归一化通量分布趋势图。从图中也可以发现中子在组件内分布与边通量分布存在较大的梯度。根据TPFAP的计算得出组件M的热群和快群不连续因子分别为1.333、1.085，组件N的热群和快群不连续因子为：0.868、1.008。由此进一步说明了船用反应堆存在显著的非均匀性。

3.2 围板/反射层组件等效均匀化参数计算

船用压水堆堆芯周围设置有一定厚度的不锈钢围板，由于不锈钢具有大的吸收截面，因而围板对堆芯的功率分布有很大影响，尤其是对靠近它的组件影响更为突出。先进均匀化理论通过引入超组件计算[2]可以计算获得围板/反射层的中子泄漏谱，并利用入射中子流为零或边界中子通量为零的边界条件求出不连续因子。根据船用堆堆芯布置，我们将围板/反射层与相邻组件组成的超组件分为：①同时为水洞栅元，②同时为控制棒栅元，③时含有水洞和控制棒栅元三种情况进行计算。图2为其中超组件③计算的简化布置图。计算结果见表1。

4 计算结果与分析

验算一、冷态临界下，计算四组棒和五组棒从归一化棒位入落入堆芯时产生的总的积分价值；验算二、热态不同临界棒位下，计算四组棒的积分价值。计算结果见表1、表2，从结果看考虑控制棒在堆芯的分布状态对围板/反射层的影响后可以将积分价值的计算误差控制在 2% 以内，尤其对大距离移动的控制棒组的积分价值计算有明显改进。

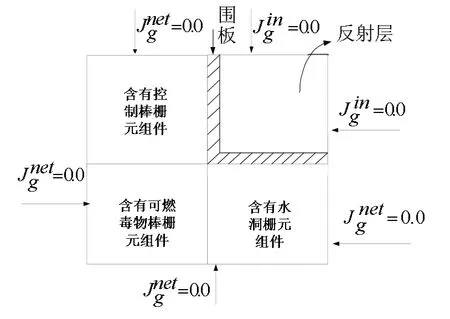
图2 超组件示意图

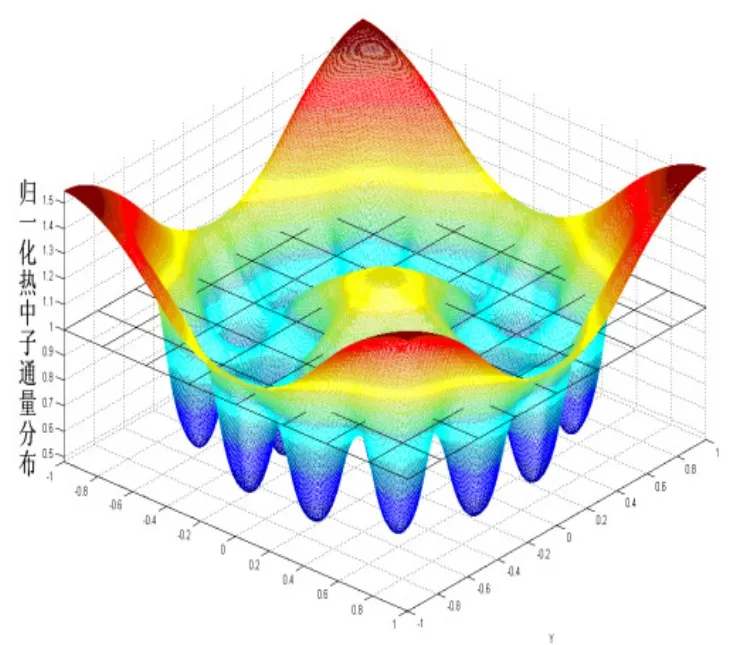
图3 组件M热中子归一化分布图

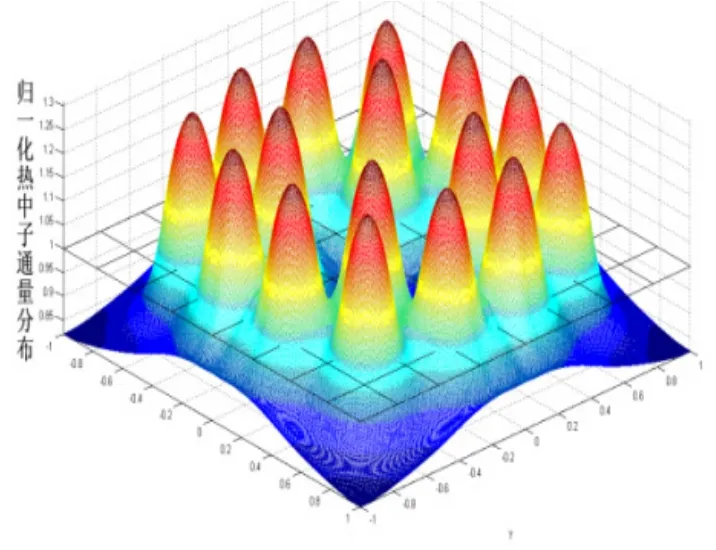
图4 组件N热中子归一化分布图

总的来说，不连续因子的计算和控制棒积分价值验算结果进一步说明了船用压水堆具有显著的非均匀性。船用压水堆的非均匀性主要由反应堆本身的堆结构所决定，同时控制棒在堆芯的分布也会对反应堆的非均匀性产生一定的影响。船用压水堆堆芯最外层组件均是由含有多束控制棒的组件组成（分为四组和五组），组件本身含有强吸截面材料使组件产生了较大的非均匀性。同时四组和五组控制棒作为功率调节棒组，它们的棒位变化使堆芯中某一区域由含多束控制棒的组件变为含多个水洞的组件，影响了堆芯外层组件的快中子谱和热中子谱以及堆芯外层泄漏中子谱的分布，也是反应堆存在显著非均匀性的原因。充分考虑控制棒分布对围板/反射层等效均匀化参数的影响是必要的。

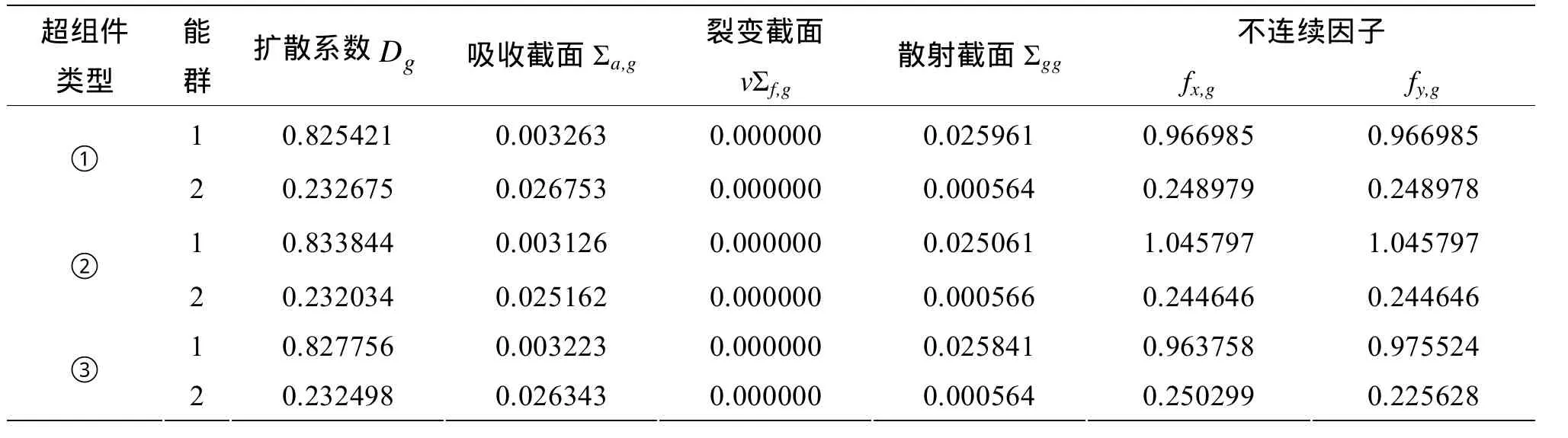
表1 冷态围板/反射层等效均匀化参数

表2 冷态临界下的积分价值计算结果

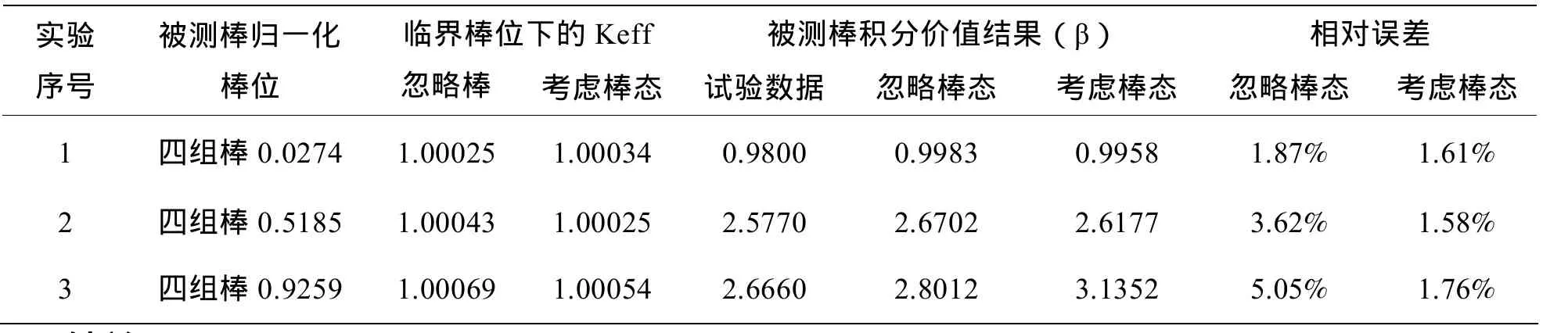
表3 热态临界下的积分价值计算结果

5 结论

1) 利用 TPFAP程序并通过添加的函数模块成功地计算出了燃料组件以及围板/反射层的不连续因子。

2) 经计算可知船用堆存在显著的非均匀性，引入不连续因子理论能有效改善控制棒的计算精度。

3) 船用压水堆的不均匀性除了与反应堆结构紧密相关外，还受到堆内控制棒分布变化的影响。

4) 通过计算结果与试验的比对，文章进一步验算了 NLSANM程序对船用堆的适用性和正确性。

[1]K.S. Smith. Assembly homogenization techniques for light water reactor analysis. Progress in Nuclear Energy, 17(13): 303-305, 1986.

[2]谢仲生. 压水堆核电厂堆芯燃料管理计算及优化[M]. 原子能出版社, 2001.

[3]周旭华. 高温气冷堆控制棒区不连续因子的计算与应用[J]. 核动力工程, 2008, 29(6): 1-5.

[4]廖承奎. 求解稳态中子扩散方程的非线性迭代半解析节块程序NLSANM程序手册. 西安: 西安交通大学, 2002．

[5]王红霞, 铁水反射层参数均匀化计算[D]. 西安: 西安交通大学, 2002．

[6]谢仲生等, 核反应堆物理分析[M]. 北京: 原子能出版社, 1994．