变抽头均衡电抗器研究

杨文铁 杨勇 耿攀 徐正喜

（武汉第二船舶设计研究所，武汉 430064）

0 引言

整流负载产生的大量非线性谐波源是影响电磁兼容性一个非常突出的问题。消除这种现象的一个有效的方法是使用带有变抽头均衡电抗器的多相整流电路，它可显著提高整流电路的各方面特性,而其结构仅仅是在传统整流器的基础上增加几个开关器件。文献[1、2]对带双抽头均衡电抗器的六相整流电路的结构，电压、电流特性作了较为详细的分析计算，本文在此基础上重点研究该整流电路的核心器件--变抽头均衡电抗器。对变抽头均衡电抗器的结构进行了分析，建立了其在Matlab中的仿真模型，研究了均衡电抗器上变抽头取不同个数和处于不同位置时，对电路特性的影响，得到了变抽头的最优变比值。

1 变抽头多相整流系统

带双抽头均衡电抗器的六相整流电路最为常见，其电路结构如图1所示[1,2]。

该整流电路由三/六相变压器、两个不控三相整流桥以及二极管双抽头均衡电抗器构成。主变压器为三相三绕组变压器，一次侧为Y联结，第

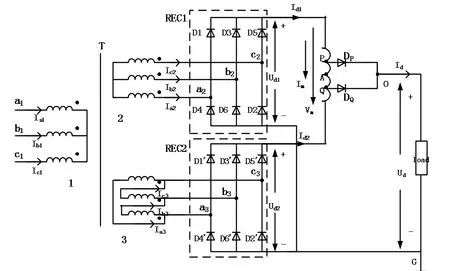
图1 双抽头六相整流系统结构图

二、三绕组分别为Y、∆联接，两个二次绕组对应的交流线电压相位相差 30°。为使两整流桥直流输出电压平衡，取三个绕组相对匝数比为N1∶N2∶N3=1∶as/3∶as，其中as=N3/N1。

二极管双抽头均衡电抗器为该电路的核心器件，对其合理的设计可以平衡两个不控三相整流桥的输出电压，增加输出直流电压脉波数，实现24脉波整流以减少输出电压的脉波系数和纹波系数，同时降低输入交流电流的谐波含量以减少电磁干扰。

当抽头数为3个时电路结构图如图2（a）所示，由于副边Y与∆绕组对称，A点处于均衡电抗器的中点，而且二极管为不可控开关器件，因而二极管DA一直处于关断态，DP、DQ管在自然换相点处交替导通，所以抽头数为3时与双抽头结构的电路等效。当抽头数为4时，电路结构如图 2(b)所示，当Ud1＞Ud2时，DQ、DQ1、DP1关断，DP导通；当Ud1＜Ud2时，DP、DQ1、DP1关断，DQ导通,所以此时也与双抽头时电路特性一样。同理，可以分析更多抽头数时的情况，得到结论当使用不控开关器件时，电路只能实现 24脉波整流。

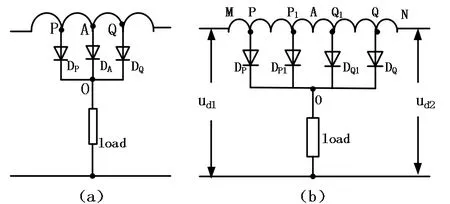
图2 多抽头时的电路结构图

当采用可控开关器件时，相对于采用不控开关器件的电路，影响电路特性的因素除了均衡电抗器变比的大小，还有开关器件的动作时间。

当采用可控开关器件且抽头数为2时，电路结构如图3（a）所示，取合适的变比和相控角，该整流电路输出直流电压为24脉波，而且可获得比采用不控开关时更优的电路特性。

当采用可控开关器件且抽头数为3时，电路结构如图3(b)所示，该整流电路有三种工作模式，分别是P管导通，A管导通和Q管导通。在各工作模式下UAO、Im的大小分别如下：

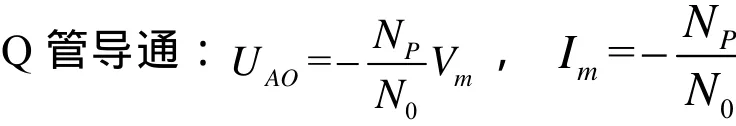
其中：Vm表示均衡电抗器两端的电压，Id表示流过均衡电抗器上的电流，如图1中所示。

改变相控角的大小可控制开关器件动作的时刻以及各个工作模式下工作时间的长短。相对于抽头数为2的电路，该结构多了A管导通这种工作模式，因而输出直流电压脉波数可达36脉波，电路特性有了进一步提高。

当抽头数为4时，输出48脉波，类似可分析更多抽头数时的电路工作情况[1,3]。所以，当采用可控开关器件时，随着变抽头数的增加输出直流电压脉波数会增加，电路特性更优，但同时系统的体积和重量也会相应增加，因而需根据实际情况合理选择。

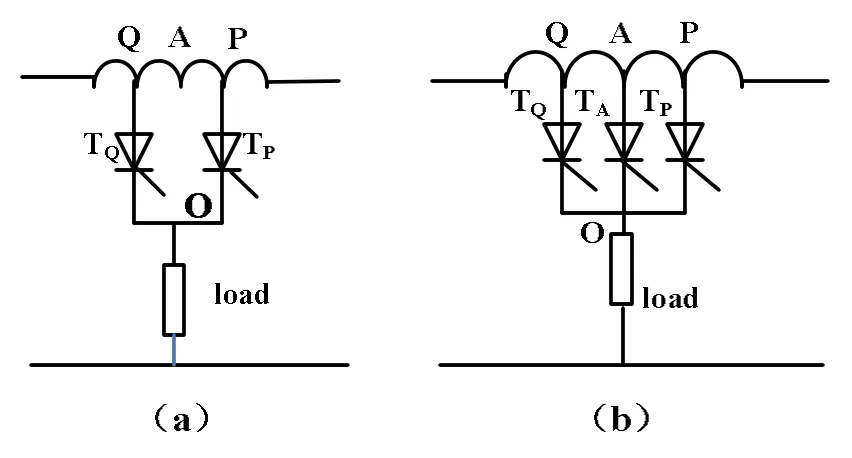
图3 使用可控开关器件时的变抽头整流电路结构图

2 变抽头均衡电抗器仿真模型建立

关于变抽头均衡电抗器仿真模型的建立，文献[4]给出了双抽头均衡电抗器的仿真模型，该模型是基于T型去耦等效变换得到的，但该模型只适用于双抽头的情况，当变抽头数更多时，则无法使用，有局限性；文献[5]给出了多抽头均衡电抗器的仿真模型，但该模型的推导计算过程复杂，特别是当抽头数大于2个时，模型使用更是不方便。本文给出了一种简单的基于Matlab中多互感线圈模型的变抽头均衡电抗器的仿真模型。

以双抽头均衡电抗器为例进行分析，图4为双抽头电抗器的实物结构图，其中a、d表示输入端，b、c表示输出端，图5为双抽头电抗器的等效电路图[4]。

图6为Matlab中多互感线圈的模型，建模时可根据实际情况设置线圈的个数、自感和互感值，同时该仿真模型还可设置等效电阻，来反映线圈和铁心的损耗。以双抽头均衡电抗器为例，取多互感线圈个数为3个，其中线圈1、2、3分别等效于图5中的MP、PQ、QN段线圈，将各线圈首尾端相接，并设 a、d为输入端，b、c为输出端，如图7所示，即为双抽头均衡电抗器的仿真模型，后文通过仿真和实验证明了该模型的正确性。同理可以建立更多抽头数时的均衡电抗器仿真模型，该模型具有广泛的适用性。

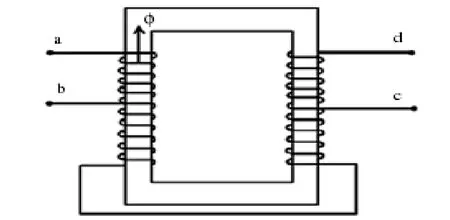
图4 双抽头电抗器的实物结构图

图5 双抽头电抗器的等效电路图

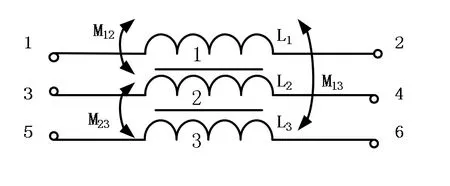
图6 Matlab中互感线圈的模型

图7 双抽头电抗器的仿真模型

3 变抽头最优变比的确定

以双抽头均衡电抗器为例，首先定义：NP/N0为双抽头均衡电抗器的变比，其中NP为AP段或AQ段线圈的匝数，N0为均衡电抗器总匝数，如图1所示。

在对变压器原边交流电流的分析中可以看到，由于二极管变抽头的存在电路中会产生环流，且环流大小与电抗器的变比有关。环流在减少变压器原边交流电流谐波含量、改善波形质量方面起着很重要的作用，因而变比的合理选取决定了整个整流电路特性的优劣。

根据文献[1、2]中有关整流电路输入交流电流的计算分析，进一步推导可以得到电流的傅里叶展开式为：

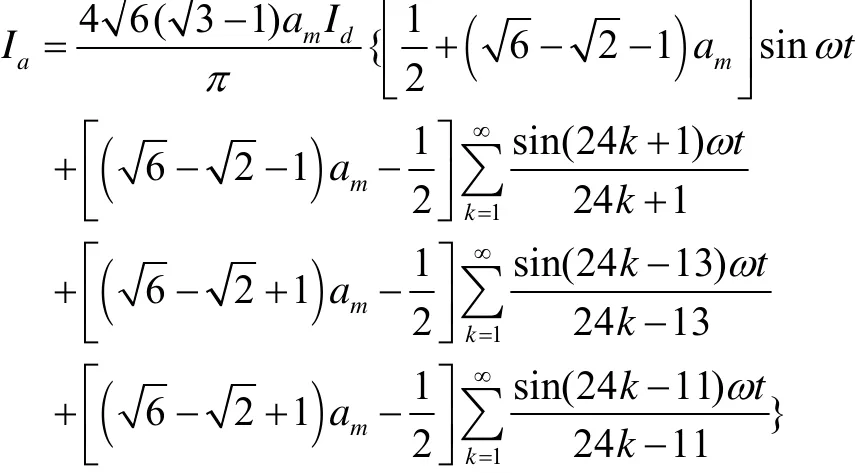
式中：am即为变抽头变比NP/N0，Id为输出直流电流，如图1中所示。

从电路输入交流电流的表达式可以看到，当am=0.246时，可消除系统的11次和13次谐波。

然后再分析输入交流电流THD最小时的变比am的取值。网侧电流的THD值可以表示为:

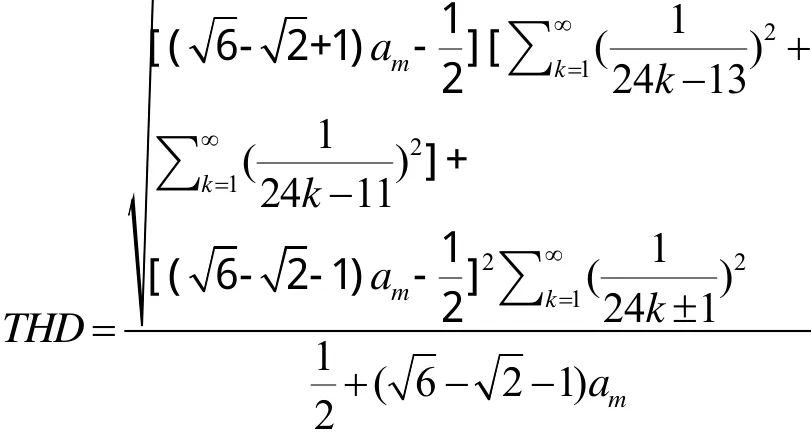
从该式可以看到THD是am的函数，为了使THD最小，对am求导，并令导数为零，可得到am=0.246，即此时THD最小，且谐波中含有的最低次谐波为23次。

同理，可分析当am=0.25时, 电压脉动系数、电压纹波系数最小。综合考虑，可取am=0.246。同时必须注意到，以上理论分析都是在不考虑变压器与均衡电抗器自身电阻的情况下得到的，但在工程实际中这些都是不可忽略的。所以在实际设计中对于不同的系统，最优变比值是不同的，需具体考虑。而且其值的大小很难通过理论计算得到具体的变化规律，解决办法是通过仿真来确定变比的最优值。

4 仿真与实验结果

为了验证仿真模型的正确性，以双抽头电抗器为例进行了相关仿真和实验。均衡电抗器两端电压的仿真与实验波形分别如图8、9所示，流过抽头二极管电流的仿真与实验波形分别如图10、11所示。仿真得到均衡电抗器两端电压和流过抽头二极管电流的波形与实验测得的波形是一致的，所以可证明该模型的正确性。同时从流过抽头二极管上的电流波形可以看到，两个二极管轮流导通，使电路由原来的12脉波增加到24脉波，改善了电路特性。该模型对于更多抽头数的均衡电抗器同样适用。

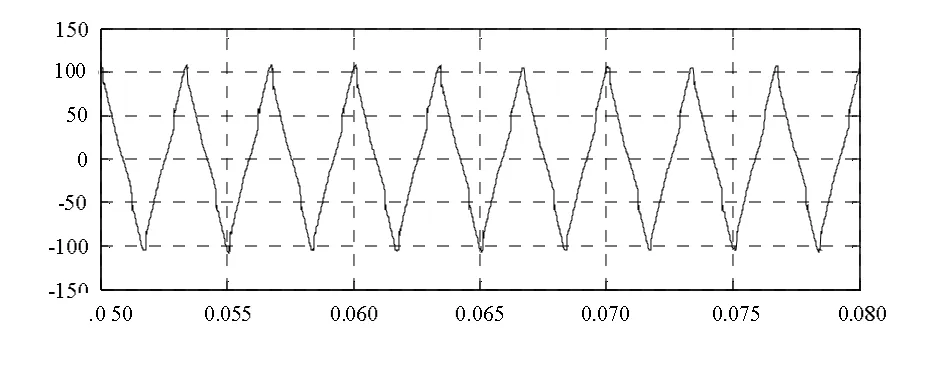
图8 均衡电抗器两端电压的仿真波形（50 V/div, 0.005 s/div）

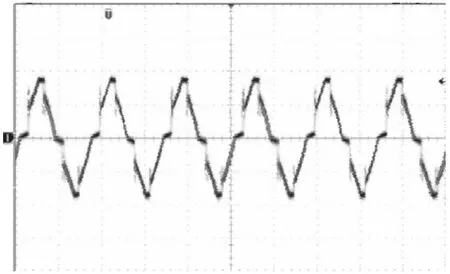
图9 均衡电抗器两端电压的实验波形（56 V/div, 0.001 s/div）

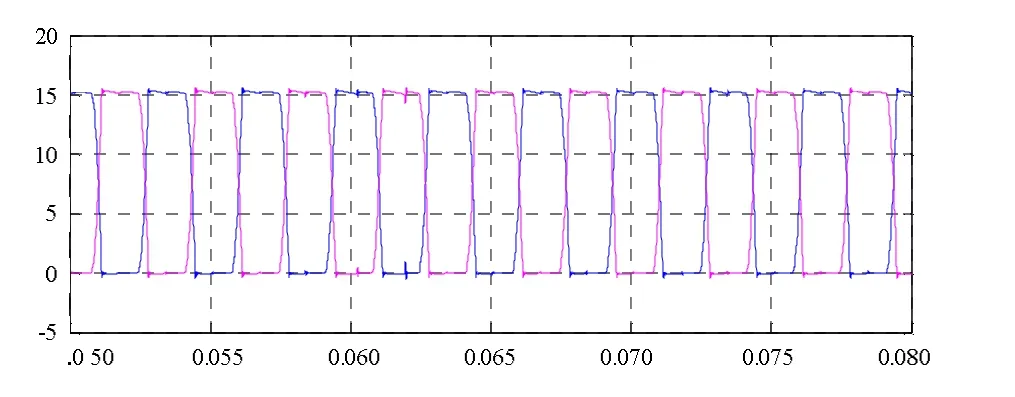
图10 流过变抽头二极管上电流的仿真波形（5 A/div, 0.005 s/div）

5 结论

本文对变抽头均衡电抗器进行了详细的研究，给出了其基于Matlab中多互感线圈的仿真模型，该模型的建立对带有变抽头均衡电抗器的整流系统分析、参数选定以及设计提供了方便，具有重要的工程应用价值；研究了不同抽头数以及不同抽头变比时，电路的不同特性，得到了最优变比值，为工程设计中抽头位置和个数的确定提供了指导。

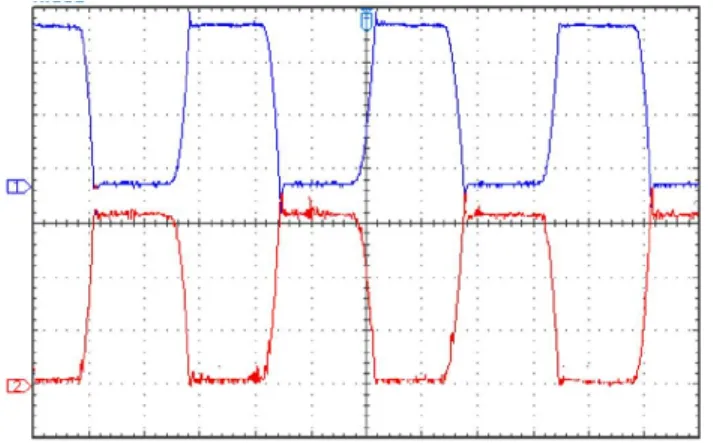
图11 流过变抽头二极管上电流的实验波形（5 A/div, 0.001 s/div）

[1]Shota Miyairi, Shoji Iida, et al. New method for reducing harmonics involved in input and output of rectifier with interphase transformer. IEEE Trans.on Industry Application, 1986, 22(5): 790～797.

[2]潘启军, 刘德志. 变抽头六相整流系统的分析. 中国电机工程学报, 2003, 23(12): 146～152.

[3]Bhim Singh, Senior Member, IEEE, Sanjay Gairola,Brij N.Singh, Member, IEEE, Ambrish Chandra,Senior Member, IEEE, and Kamal Al-Haddad, Fellow,IEEE. Multipulse AC–DC converters for improving power quality: A Review. IEEE Transactions on Power Electronics, 2008, 23(3): 260- 281.

[4]Q. Pan, W. Mav, and D. Liu. A new critical formula and mathematical model of double-tap interphase reactor in a six-phase tap-changer diode rectifier.IEEE TransInd. Electron. 2007, 54(1): 479-485.

[5]Fangang, Meng, Shiyan, Yang, and Wei, Yang Member,IEEE. Modeling for a multitap interphase reactor in a multipulse diode bridge rectifier. IEEE Transactions on Power Electronics, 2009, 24(9): 2171- 2177.