关联分析法在筛选参后地土壤敏感因子上的应用
2012-09-21刘春红
刘春红
(长春大学光华学院 基础教研部,长春 130033)
0 引言
人参是传统的中药,是名贵的药用植物。人参是宿根植物,忌地性极强,不能重茬,而且还不能连作,因为参后地土壤的养分、土壤理化性质等诸多因素都发生了变化,这些因素是响人参产量的主要原因。在这些因素中哪些是主要的,哪些事次要的,哪些需要利用和发展的、哪些需要抑制和避免的,哪些是潜在的、哪些是明显的,本文将通过灰色系统中的关联分析来确定哪些因素敏感,利用关联分析方法,将关联度大的因子确定栽参地土壤的环境质量敏感因子。
1 人参根重及非生物因子变化
1.1 人参根重增长变化规律
人参根重的年积累变化规律符合S型自然生长曲线,即与Logistic增长曲线的变化规律相近似。人参根重变化最符合的S型曲线是

其中:y表示人参根重(g);t表示人参生长年限。
本文将选用这个已有的研究结果,其函数表达式能够更好地反映人参根重与生长年限之间的关系,确切地反映了人参根重积累的年变化规律。
根据上述结果,通过运算可得人生根重不同年份的重量变化表1。

表1 不同年份人参根重变化
1.2 有机质、碳氮比等非生物因子变化特征
参后地土壤逐渐退化过程中,土壤有机质3年下降幅度为13.0-19.4%,全氮含量3年下降幅度为8.9-18.4%。栽参后土壤C/N比下降,效磷和磷栽参后没有明显的变化规律。不同栽参年限里,有机质、碳氮比等非生物因子变化如表2。

表2 不同栽参年限里,有机质、碳氮比、等非生物因子变化

续表
由表2[2]可见,随栽参年限的增加,土壤有机质和全氮含量下降,三年时下降幅度分为13.0~19.4% 和8.9~18.4%,栽参后土壤C/N比下降。
2 敏感因子筛选
2.1 研究方法
本文采用灰色系统理论分析方法,灰色系统理论[3]是20世纪80年代,由中国华中理工大学邓聚龙教授首先提出并创立的一门新兴学科,它是基于数学理论的系统工程学科。主要解决一些包含未知因素的特殊领域的问题,它广泛应用于农业、地质、气象等学科。
灰色预测法[3-5]是一种对含有不确定因素的系统进行预测的方法。本论文研究栽参地土壤质量敏感因子对不同年份参根重的反应,采用灰色关联度方法[4]进行分析。灰色系统理论提出了一种新的分析方法—关联分析方法,即根据因素之间发展态势的相似或相异程度来衡量因素之间的关联程度,它揭示了事物动态关联的特征与程度。根据灰色系统理论,关联度分析是一种相对性排序分析,是用于分析各因素之间随着时间变化的动态关系及其特征的定量方法。判断因素间的关联程度,从而分析哪些因素关系密切,哪些因素不够密切。并用关联系数、关联度和关联序来表示。具体步骤如下:
(1)对单位不同或初值不同的数列进行处理.使之无量纲、归一化;
(2)求关联系数中的两级差:参考数列x0与直接比较数列xi在第k点的绝对差Δ(k)为Δ(k)=|x0(k)-xi(k)|,在第xi找出各点与x0的最小差,是第一级:

在各条曲线中找出的最小差的基础上再按i=1,2,…,m,找所有xi曲线中的最小差:
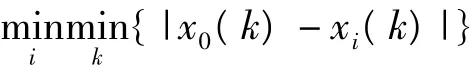
是第二级最小差。找两级最大差的方法与找两级最小差的方法相似:
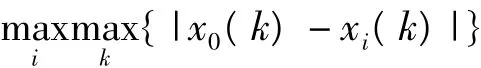
是两级最大差。
(3)求关联系数:参考数列与直接比较数列在第k点的关联系数为:

式中,ρ为分辨系数。ρ⊂[0,1],ρ越小,分辨率越高。分辨系数ρ的取值与分辨率成反比,ρ小,分辨率大;ρ大,分辨率小。ρ的取值大小关键在于控制ξi(k)的散布范围。原则上,ρ可取值(0,+∞),而通常可依不同需求考虑其取值。若使ξi(k)散布区间的长度不小于0.5,则应限制ρ∈[0,1]。当ρ≤0.5263时,较容易观察关联度分辨率的变化,故通常应取值ρ=0.5。
(4)求关联度:综合各点的关联系数,得到整个xi曲线与参考曲线x0的关联度,即:

关联度ri大小表示了比较数列与参考数列的密切程度,ri越大比较数列与参考数列关系越密切;反之依然。
2.2 有机质等敏感因子的筛选
栽参后土壤养分含量的变化如表4[2]。
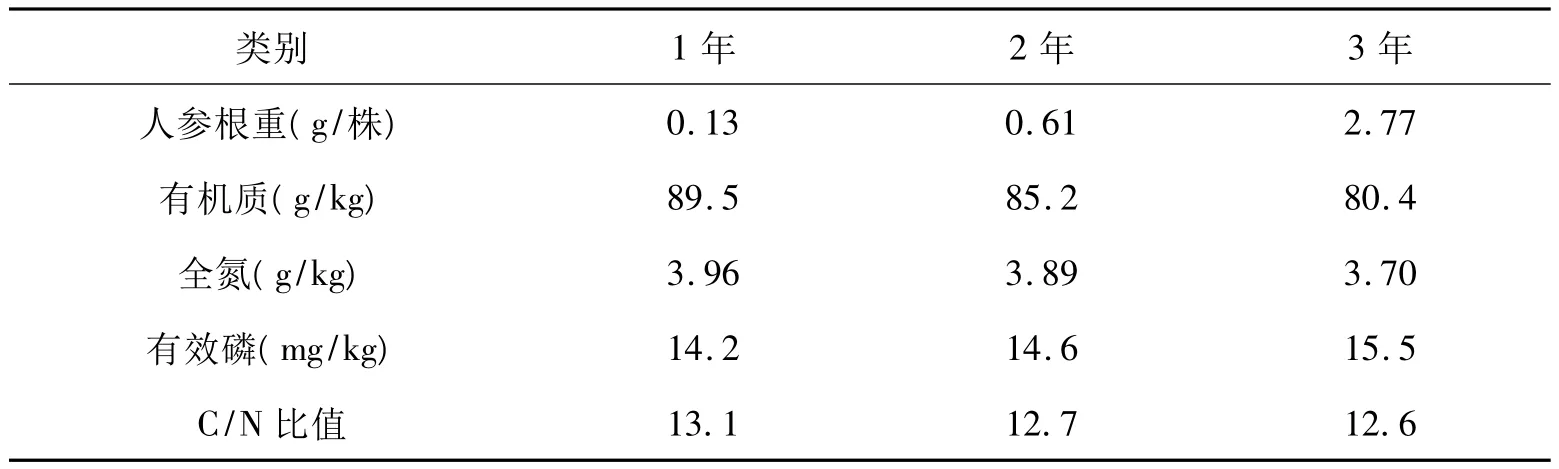
表4 栽参后土壤养分含量的变化
构造初始化数列,设原始数列为

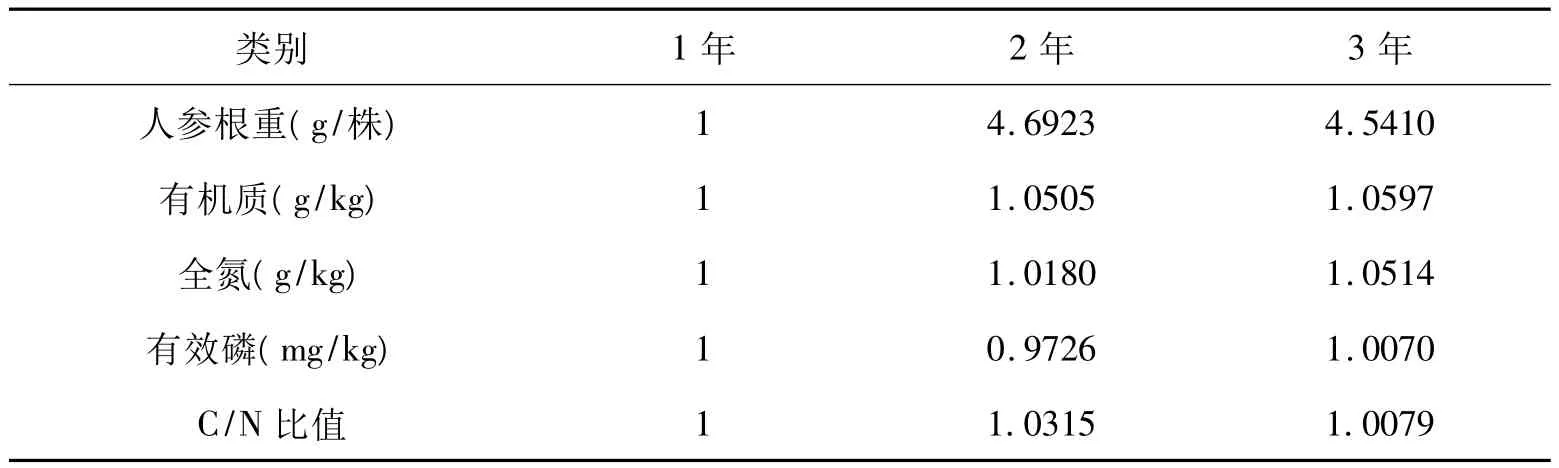
表5 有机质等因子的初始化数据
接下来利用(1-2)求关联系数,利用(1-3)求关联度(取ρ=0.5)
运用上述方法,有机质的关联度求解过程如下:

运用同样方法,可得到全氮、有效磷、及碳氮比的关联度分别为:r2=0.56125,r3=0.55938,r4=0.55991。
3 结语
本文通过关联分析方法,得到人参根重关联度大小依次为r1、r2、r4、r3,影响人参根重的主要因素依次为:有机质,全氮,碳氮比,有效磷。我们确定关联度大前三项因子,即有机质全氮、全氮、碳氮比这三个因子为影响人参根重变化的敏感因子。
[1]陈丽梅.人参生长的土壤理化环境及生长模型研究[D].长春:吉林大学,2007.
[2]窦森,张晋京,等.栽参对土壤化学性质的影响[J].吉林农业大学学报,1992,14(2):42-47.
[3]陈东彦,李冬梅,等.数学建模[M].北京:科学出版社,2007.
[4]沈继红,施久玉,等.数学建模[M].哈尔滨:哈尔滨工程大学出版社,2000.
[5]戴明强,李卫军,等 .数学建模及应用[M].北京:科学出版社,2007.
