一种基于小波变换和Canny算子相结合的边缘检测方法
2012-09-21薄胜坤张丽英
薄胜坤,张丽英
(1.长春理工大学 电子信息工程学院,长春 130022;2.长春大学 电子信息工程学院,长春 130022)
0 引言
图像边缘是分析处理图像的基础,在Marr的计算机视觉系统中,图像边缘提取占据着重要的位置,它处于系统的最底层,为其他模块服务,是图像分割、视觉匹配等研究内容的基础。边缘提取结果的优劣直接影响着图像分析、目标识别等后续工作的进行。
图像的边缘是图像灰度的奇异点和突变点,也就是图像灰度发生急剧变化的区域。图像灰度的变化情况可以用图像灰度变化的梯度来反映,因此图像的边缘提取可以由图像局部微分算法来得到。根据这一理论,众多学者在研究图像边缘提取时提出了许多现在被认为是经典的边缘提取算子,其中尤为突出的是基于最优化理论的Canny边缘检测算子。然而对图像直接使用Canny算子进行边缘提取会得到许多虚假边缘,因为对于一副待处理的图像,不可避免的会受到输入转换器件及周围拍摄环境等因素的影响,图像中不可避免的混入各种突变干扰,从而干扰图像边缘的准确提取。因此如何利用现有的经典算法提高边缘提取的准确性使边缘提取算法具有更高的信噪比是图像处理的经典难题。
本文利用小波变换具有的能够检测局部突变的能力,结合其多尺度聚焦的功能,可以很好的剔除边缘干扰,与此同时,合理的对图像做灰度增强处理,可以调整图像中目标与背景的对比度,从而再使用最优阈值下的Canny算子做边缘提取时能够达到非常好的效果。
1 理论基础
1.1 小波变换
小波变换的思想源于伸缩和平移方法。在实际运用中,尤其在计算机上实现时,连续小波变换必须加以离散化。在离散化中a总是默认只取正值。通常,把连续小波变换中的尺度参数a和平移参数b的离散化公式分别取作a=,b=kb0,这里j∈Z,扩展步长a0一般取值2,所以对应的离散小波函数为

而离散化的小波系数则可表示为:

图像是二维信号,需将以上一维小波变换推广到二维才能将其应用到图像处理中。设φ(x)为一个一维尺度函数,Ψ(x)为相应的小波函数,则二维小波函数的基础小波函数为Ψ1(x,y)=φ(x)Ψ(y),Ψ2(x,y)=Ψ(x)φ(y),Ψ3(x,y)=Ψ(x)Ψ(y),Ψ4(x,y)=φ(x)φ(y)。小波变换用于图像分析的基本思想就是把图像进行多分辨率分析,将图像分解为不同频率的子图像,对各频率图像分别进行相应的处理。
小波的二尺度分解如图1表示:
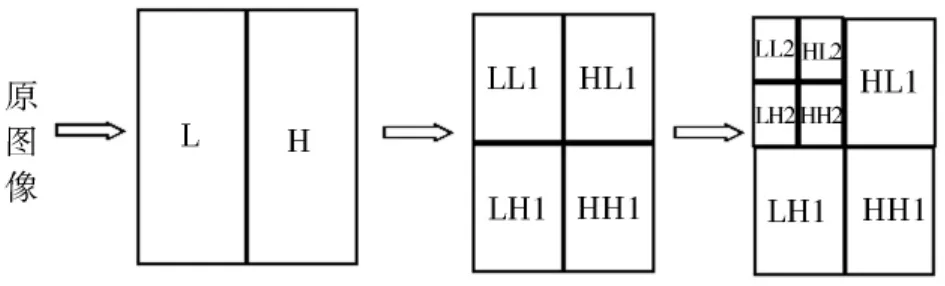
图1 小波的二尺度图像分解图
其中H表示低频,L表示高频,1、2表示一级或二级分解。
1.2 Canny算子
(1)Canny算子提出了边缘检测算子的如下3个准则:
①信噪比准则。图像的信噪比越大,提取的边缘质量越高。
②定位精度准则。边缘定位精度L越大表明边缘的定位精度越高。
③单边缘响应准则。为了保证边缘只有一个响应,检测算子的脉冲响应导数的零交叉点平均距离D(f)应满足:
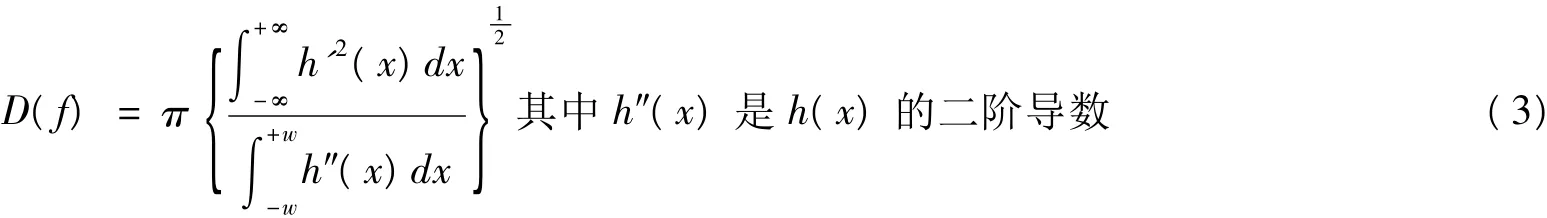
(2)以上述三个准则为基础,将这三个准则相结合可以获得最优的检测算子,具体的算法思想如下:
①用高斯滤波器平滑图像;
②用一阶偏导的有限差分来计算梯度的幅值和方向;
③对梯度幅值进行非极大值抑制;
④用双阈值算法检测和连接边缘。
2 小波变换用于去噪与图像增强及Canny算子提取边缘
2.1 小波去噪
二维小波分析用于图像消噪的步骤为:
(1)应用小波变换分解图像信号 在这一步中,选择合适的小波和恰当的分解层次(记为N),然后对待分析的二维图像信号进行N层分解计算。根据小波的选取原则,本文选取coif4小波,并取N=3。
(2)对分解后的高频系数进行阈值量化 对于分解的每一层,选择一个恰当的阈值,并对该层高频系数进行软阈值量化处理。本章中对于阈值的选取采用Donoho提出的最优阈值获取理论,阈值的选择满足:T=采用改进的软阈值量化方法:
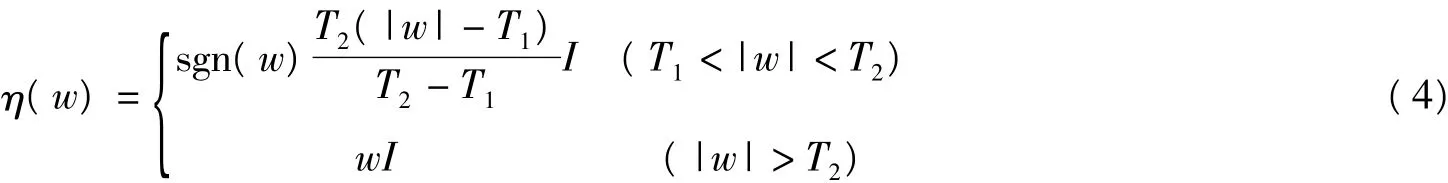
其中0<T1<T2。
(3)二维小波的重构图像信号利用经过处理后的各层小波系数进行小波重构。
2.2 小波图像增强
小波变换将一副图像分解为大小、位置和方向均不相同的分量,在做逆变换之前,可根据需要对目标和背景上的分量改变其系数的大小,从而使得其对比度增加。本章中将图像小波变换系数的低频部分进行增强,高频部分进行衰减。
2.3 Canny算子提取边缘
Canny算子提取边缘的具体步骤:
(1)通过对比选择,选取参数σ=2的高斯函数对图像进行平滑处理。
(2)图像的灰度梯度的幅值A(i,j)和方向θ(i,j)的计算公式为:
其中X(i,j),Y(i,j)分别为图像灰度梯度的近似X,Y方向的偏导。
(3)对图像中的每一个像素点,以该点为中心,在八邻域范围内分析相邻两点在式(7),(8)中得到的A(i,j)和θ(i,j)值,在梯度方向上只保留幅值最大值点,其他幅值设置为零。
(4)针对图像的梯度幅值取两个阈值,先用大阈值判断出图像的大致轮廓,再用小阈值判断出图像的细节轮廓,用细节轮廓进行边缘追踪丰富大致轮廓,最终提取图像轮廓。
用Canny算子提取图像边缘,重点在于阈值的选取。本文采用最优阈值获取算法。该算法的思想是,一幅图像的边缘点分为端点和中间点,端点的8邻域内最多只有两个二值化的1,其余的都为0,中间点的八邻域内至少有两个二值化的1,根据这一规则,在选取阈值时,先选用一个较小的阈值,对图像进行二值化处理,标记二值化图像中边缘的端点和中间点,增加阈值,标记该阈值下边缘的端点和中间点,比较前后两个阈值下端点数目的变化情况,若几乎无变化,则继续加大阈值,直到出现大的变化为止。至此,倒数第二次选取的阈值为最优阈值。
3 实验仿真结果

图2 原图像

图3 含噪图像

图4 小波去噪增强图像

图5 (Canny)检测边缘(0.1)

图6 (Canny)检测边缘(0.1)

图7 本文方法(最优阀值0.13)
上图中,图2为原始图像,图5为该图像对应的阈值取0.09的Canny检测边缘,图3为含高斯噪声的图像,图6为其对应的检测边缘。对比图5与图6可知,直接对含噪图像进行Canny边缘检测,检测效果很差。图4为小波去噪增强图像,与图2相比,可见去噪效果很好。图7为采用本章方法检测的图4的边缘。对比图5、6、7三图可知,采用本文方法检测图像边缘比直接采用Canny算子检测的效果好的多,与不含噪声图像的检测结果相比,效果相差不多。
仿真结果表明,本文所用方法可以很好的消除因噪声干扰带来的虚假边缘,强化弱边缘,能够很好的把图像边缘检测出来。
[1]朱志刚,石定机,等译.数字图像处理[M].北京:电子工业出版社,1999.
[2]胡晓峰,赵辉,编著.Visual C++/MATLAB图像处理与识别实用案例精选[M].北京:人民邮电出版社,2004.
[3]飞思科技产品研发中心编著.MATLAB6.5辅助小波分析与应用[M].北京:电子工业出版社,2003.
[4]陈武凡,编著.小波分析及其在图像处理中的应用[M].北京:科学出版社,2003.
[5]周伟,桂林,周林等编著.MATLAB小波分析高级技术[M].西安:西安电子科技大学出版社,2006.
[6]王慧燕.图像边缘检测和图像匹配研究及应用[D].杭州:浙江大学,2003.
[7]连静.图像边缘特征提取算法研究及应用[D].长春:吉林大学,2008.
[8]周洪成.基于小波变换的图像边缘检测技术的改进[J].金陵科技学院学报,2009(6):31-35.
[9]刘勇,姚刚,等.自适应多窗口梯度幅值边缘检测算法[J].华中科技大学学报,2011(1):14-18.
