基于AHP分析的二级模糊综合评价模型及在边坡风险易损性评价中的应用*

虢 柱，聂春龙

(1.怀通高速公路建设开发总公司，湖南怀化 418116;2.南华大学城市建设学院，湖南 衡阳 421001)

易损性分析指分析受灾体遭受地质灾害破坏的机会与发生损毁的难易程度，是滑坡风险灾害分析的重要内容之一。受灾体易损性分析的因素众多，逻辑关系复杂，国内外学者对层次分析法、模糊分析法、灰色聚类分析法、多元多级综合评价等方法均进行了研究［1－3］。本文将层次分析法与模糊分析相结合，建立基于AHP的二级模糊综合评价模型，并用于工程实践中的易损性评价。

1 基于AHP分析的二级模糊综合评价模型

1.1 AHP分析法的基本方法和步骤

层次分析法是把复杂问题分解成各个组成因素，又将这些因素按支配关系分组形成递阶层次结构。通过两两比较的方式确定各个因素相对重要性，然后综合决策者的判断，确定决策方案相对重要性的总排序，可分为4步进行［4］:

(1)分析系统中各因素之间的关系，建立系统的递阶层次结构;

(2)对同一层次的各元素关于上一层中某一准则的重要性进行两两比较，构造两两比较的判断矩阵。

(3)由判断矩阵计算被比较元素对于该准则的相对权重，进行一致性判断;

(4)计算各层元素对系统目标的合成权重，并进行排序，

1.2 模糊综合评价

设评价等级的论域为V= {V1，V2，V3}，Vi代表各种可能的评价结果。二级评价指标中各个指标的权重向量如下。

Wj=(Wj1，Wj2，…，Wjk)，隶属度矩阵为［5］:

那么，单级评价模型为:

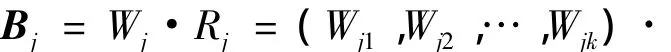
对于一级评价指标，Bj是其单因素评价结果，因此，也可以得出一级评价指标的隶属度矩阵。

根据所求的一级指标的权向量为W=(W1，W2，…，Wi)，则最终的模糊综合评价模模型为:

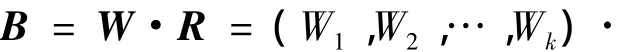
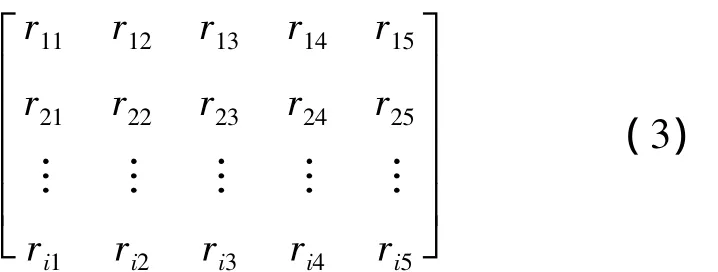
1.3 模糊综合评价等级的判定

常规的易损等级判定方法是由模糊运算结果，取评价集V的模糊子集B中向量值最大者，根据其在评价集中所处等级即为所求的评价等级。但是，该方法不能充分的利用模糊子集B中所带来的所有信息;另外，对于模糊集B中的各元素值只是相对意义而没有绝对意义，因此，考虑采用以加权平均原则对模糊综合评价结果进行处理，从而达到更真实的反应评价对象的易损性等级。采用加权平均的模式如下［6］:

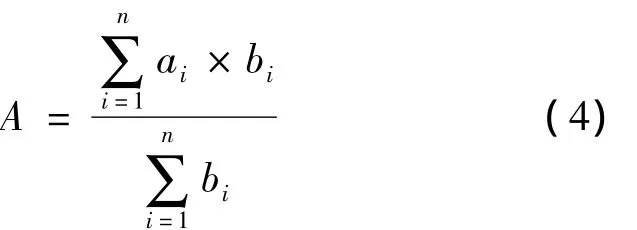
式中:A为受灾体易损指数;ai为评价因子评价级别的基准界限值。根据A判定受灾体易损性等级。

2 工程实例研究

“5.12”特大地震以后，理县营盘街小学后山斜坡的山脊部位由于应力相对集中，出现大量裂缝和局部滑动变形。根据实地调查，由于坡面植被发育，对坡面起了一定的稳固作用，山体斜坡目前并未形成统一的滑移面。通过应急勘查，查明山脊部位共有3个变形区，分布高程在1 971～2 175 m一段，变形区变形迹象明显。危害区为营盘街小学及震后临时安置板房区，学校师生及附近居民人口多达1 700余人，成灾后可能造成的经济损失在巨大，需要对营盘街小学、居民房及震后临时安置板房进行易损性评价［7］。

2.1 易损性评价指标及其等级划分

由于营盘街小学的重要性，先对其进行易损性评价分析，营盘街小学易损性评价指标及其等级划分如表1所示。

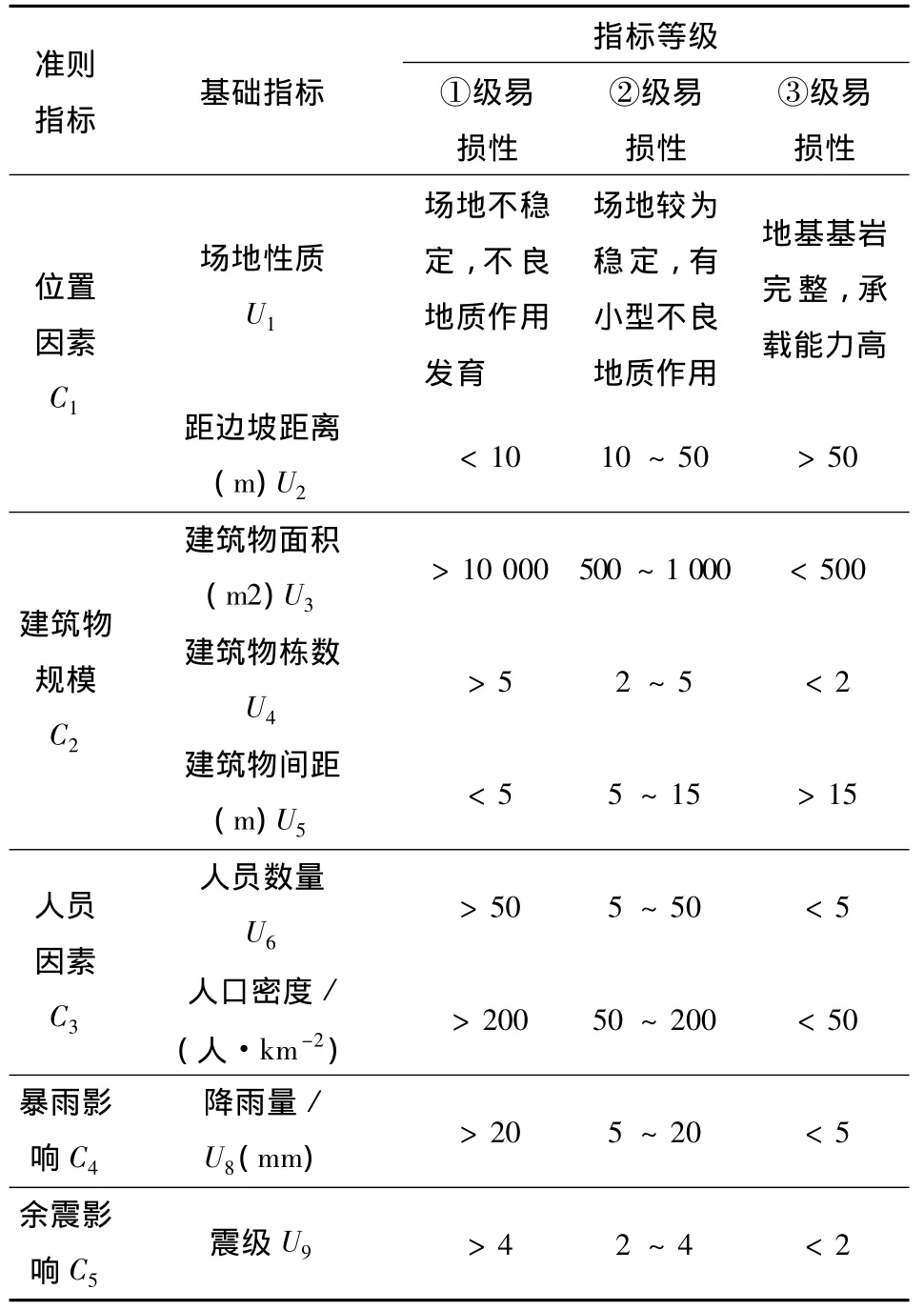
表1 营盘街小学易损性评价指标及其等级划分Table 1 Damage index and its grades of Yingpanjie school

2.2 确定评价指标的权重

根据AHP计算的各步骤，得到层次指标权重，如表2所示。经过计算，各级矩阵均满足一致性要求。

2.3 确定评价指标的模糊隶属函数及其隶属度

模糊评价充分考虑等级间的模糊状态，确定隶属函数后，使得评价结果更为接近真实值。依据隶属函数确定的原则，工程易损性采用区间形式划分等级，岭型分布函数。

营盘街小学工程易损性评价因子模糊隶属度如表3所示。

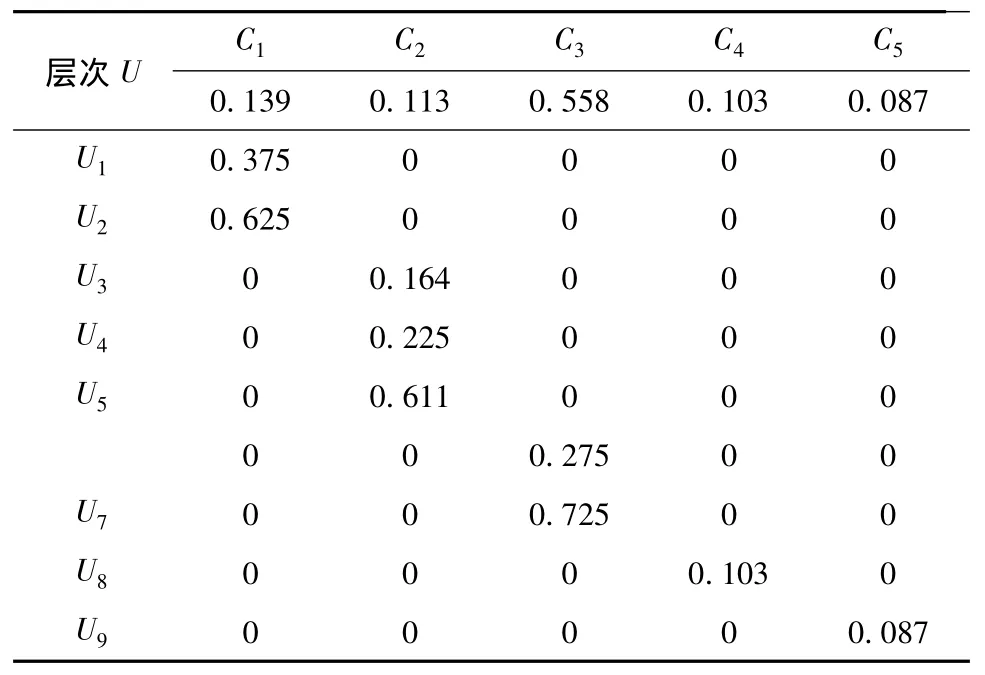
表2 层次指标权重Table 2 Index ratio of grades

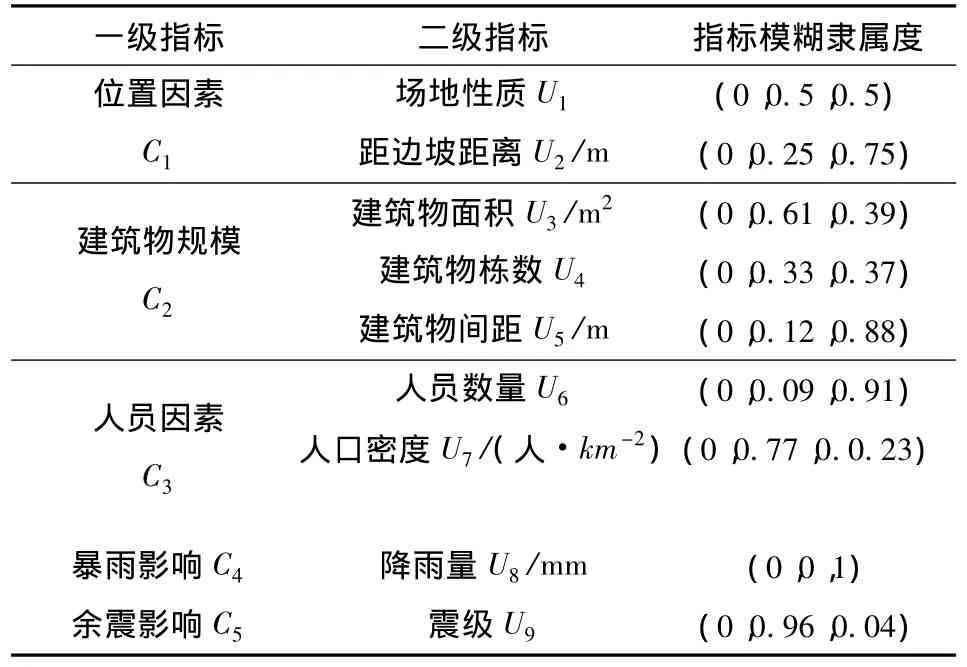
表3 营盘街小学二级评价指标隶属度Table 3 Second level evaluation membership of Yingpanjie School

2.4 易损性评价的二级模糊运算

根据布拉福德定律，以0.33为公差将受灾体损毁程度等级进行划分①级、②级、③级，具体对应权重描述见图1。

图1 损毁程度对应权重Fig.1 Corresponding weights of damage degree

由各层次指标权重值及其隶属度可构建出模糊向量，进而形成各层次指标的底层评价模糊矩阵Ri，然后根据Fuzzy模糊运算公式V=W·R计算出各个指标的二级模糊评价向量，所得结果如表4所示。

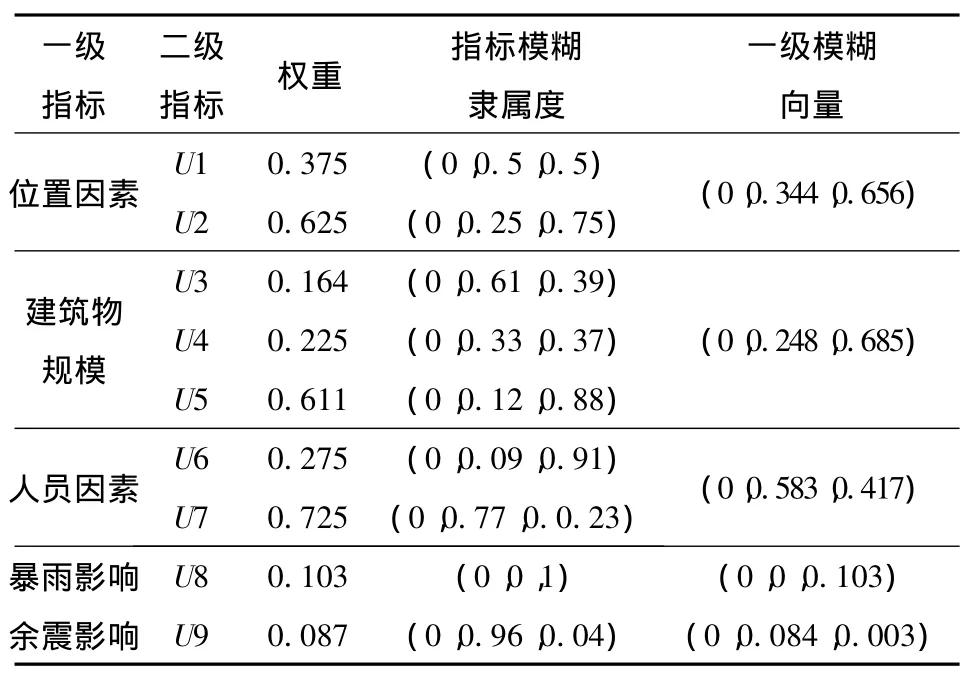
表4 营盘街小学二级模糊计算结果Table 4 Calculation results of Yingpanjie School by second level fuzzy model

2.5 易损性模糊综合评价结果

根据二级模糊运算结果进行一级模糊综合运算，计算结果如表5所示。

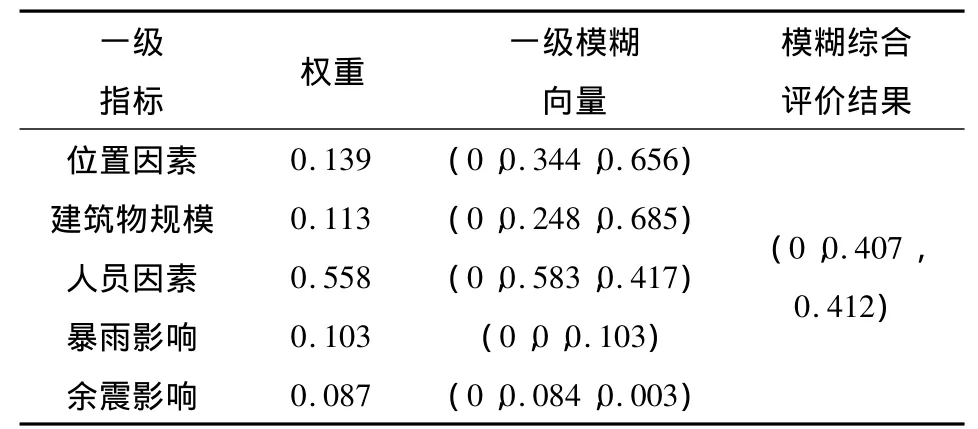
表5 营盘街小学一级模糊综合运算Table 5 Calculation results of Yingpanjie School by first level fuzzy model

根据公式(4)，可计算出营盘街小学的易损性指数如下。

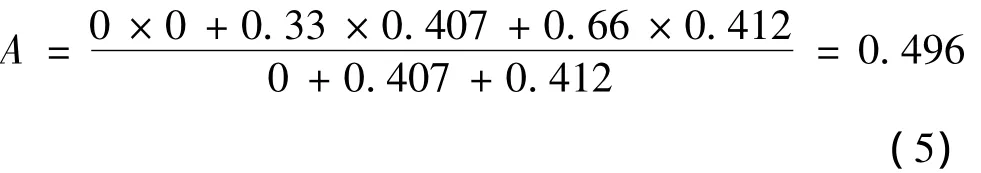
由计算结果可知，营盘街小学的易损性指数为0.496，受灾体损毁程度等级进行划分标准，它的易损性等级为②级易损。

同理，根据上述计算方法对边坡周围的民房和临时安置板房进行易损性评价，民房的易损性等级为③级易损，临时安置板房的易损性等级为②级易损。将评价结果与实地调查结果进行比较，发现两者较吻合。

3 结语

在滑坡易损性评价中，需要考虑的因素是多种多样的。本文建立了基于AHP分析的二级模糊综合评价模型，将层析分析法和模糊分析法的优点结合起来，不但引入利用了人脑对模糊现象做出的正确判断，充分发挥了专家的作用，，而且考虑了各层析因素之间的逻辑关系，使得模糊评价更加准确，减少了个人主观臆断带来的弊端。本文提出的模型简单实用，具有一定的工程应用价值。

［1］夏元友，朱瑞赓.不稳定边坡治理方案的多层次模糊群决策［J］.自然灾害学报，1998，8(1):88 － 91.Xia Yuan-you，ZHU Rui-geng.Multi－ fuzzy decision for disstable slope strengthening［J］.Journal of Natural Harzard，1998，8(1):88 －91.

［2］Zahedi F.The analytic hierarchy process:A survey of the method and its application［J］.Interaces，1986 ，16(4):18－27.

［3］Hark P T.Special issue on AHP［J］.Socio Economic Planning Sciences ，1986，20(6):57 －65.

［4］许树柏.层次分析原理［M］.天津:天津大学出版社，1988:77－82.XU Shu-bai.Analysis principle of grade［M］.Tianjin:Tianjin University Press，1988:77 －82.

［5］杨松林.工程模糊论方法及其应用［M］.北京:国防工业出版社，1996:33－45.YANG Song-lin.Engineering fuzzy method and its application［M］.Beijing:National Defence Press，1996:33 －45.

［6］陈新宇，卢新中，王 琛.昆明市地质灾害易损性模糊综合评价［J］.安全与环境工程，2012，19(2):54－57.Chen Xin-yu，LU Xin-zhong，WANG Chen.Fuzzy evaluation of vulnerability of grological harzard in kunming［J］.Safety and Environment Engineering，2012，19(2):54 －57.

［7］赵绪涛.公路灾害易损性模糊综合评价［D］.西安:长安大学，2007:41－51.ZHAO Xu-tao，Fuzzy evaluation of vulnerability of highway［D］.Xi＇an:Changan University，2007:41 － 51.

［8］聂春龙.边坡工程风险分析理论与应用研究［D］.长沙:中南大学土木工程学院，2012:36－41.NIE Chun-ling.Risk analysis theory of slope engineering and its application［D］.Changsha:School of Civil Engineering，Central South University，2012:36－41.