工程项目管理多目标均衡优化研究综述

张连营，徐 畅，吴 琼

(天津大学管理与经济学部，天津 300072)

1 前言

工程项目多目标均衡优化是工程项目管理的一个重要方面。近年来有关该领域的研究引起了学者们的广泛关注并取得了较为丰硕的研究成果。1963年Kelly J E提出的关键路径法(CPM)[1]为工程项目的工期优化提供了最基本的方法。在CPM的基础上，学者们先后提出了工程项目工期成本两目标均衡优化模型(TCTM)[2]、工期 －成本 －质量均衡优化模型(TCQTM)[3]。传统的工程项目多目标均衡优化研究中，工序的时间、成本以及质量水平被默认为确定的数值，学者们根据工程项目工期成本两个目标的函数关系性态分别构建了线性的多目标优化模型和非线性的多目标优化模型[4]。随着研究的深入和新的实际应用需求的出现，学者们发现确定条件下的多目标优化模型与工程项目实际有一定差距，一定程度上限制了模型的实用性，因此不确定条件下的多目标优化问题的研究逐渐被学者们关注。目前，不确定条件下的工程项目多目标均衡优化模型主要包括以下类型:假定工序的工期和成本执行方式有多种备选模式的多模式均衡优化模型，以模糊理论为基础的多目标模糊均衡优化，假定工期、成本变量服从随机分布的多目标随机均衡优化以及多目标鲁棒均衡优化等。目前，两类模型主要通过智能优化算法来解决;相对传统的解决方法，新的智能优化算法的出现使多目标优化的问题得以深化和延展。本文将主要针对有关工程项目多目标均衡优化的模型进行综述，有关模型的算法将不作为本文的重点。

2 确定条件下的工程项目多目标均衡优化模型

针对工程项目多目标均衡优化问题，学者首先研究工程项目工期－成本两目标均衡优化模型，该类模型的目标包括在给定工期条件下寻求最小成本、在不超过既定预算的前提下寻求工程最短完成工期以及找出工期－成本均衡优化曲线。Feng C W等针对大型工程项目建立了工期－成本两目标均衡优化模型，并引入了遗传算法对模型进行求解[2]。Feng C W能够给出工期－成本两目标均衡优化模型的优化曲线[2]，但该均衡优化模型是建立在线性规划的凸包理论基础上的，成本指标只考虑了直接成本，因此所求得的最优解不一定是真正意义上的最优解。

李红仙等结合价值工程理论建立了动态工期成本均衡优化的数学模型，由于考虑了资金的时间价值，模型的实际意义和可靠性都得到了提高[5];Li H等根据不同的假设前提，分别以工期成本间的线性函数关系和二次曲线关系为基础，建立了多个均衡优化模型，并结合遗传算法对其进行了求解[6，7]。Zheng D X M等分析了已有的关于工程项目优化问题的研究，改善了前人模型中的目标函数，以工程项目的最短工期和最高的利润为目标构建了工程项目工期－成本均衡优化模型，利用基于改进的遗传算法对模型进行了求解[8]。除利用遗传算法对问题进行求解，还有一些学者利用蚁群算法[9]和微粒群算法[10]在原有模型的基础上对问题进行了探索和研究并与前人的研究[11]进行了比较。

由于实际工程项目管理的需要，并随着新的法律法规的出现也对工程建筑业提出更高的要求，工程项目的质量等因素越来越多地被关注。在工程项目工期－成本两目标均衡优化模型的基础上，学者们将质量目标加入到模型中，构建了工期－成本－质量多目标均衡优化模型，但与工期、成本指标不同，工程项目的质量目标较难量化，因此对于工期－成本－质量三元多目标优化模型而言，如何将质量指标定量化是对其进行研究的前提。Babu A J G和Suresh N最早建立了工程项目工期－成本－质量多目标线性规划模型。学者将项目各工序的质量水平定义成[0，1]之间的数，通过对所有工序的质量水平求平均值得到整个工程项目质量水平[3]。Khang D B和Myint Y M[12]利用项目实例对Babu A J G和Suresh N[3]的质量模型进行了检验，认为成本 －工期、质量－工期之间的线性关系不能很好地反映工程实际。但是Babu A J G和Suresh N[3]首次考虑了质量这一目标，并为工程项目质量的定量描述及工期、成本、质量均衡优化模型的构建提供了重要方法。Ghodsi R等建立了工程项目工期与质量间的线性函数，并以项目工期、质量作为自变量建立了非线性的成本函数

学者利用ε约束法求得Pareto最优解前沿，给出了在工期、成本和质量某一个目标确定的前提下，关于另外两个目标的均衡优化曲线[6]。该模型使项目工期、质量两个目标成为自由变量，提高了模型变量的自由度，更加接近工程实际。陈勇强等结合工程项目实际构建了项目均衡优化模型并分别利用蚁群算法和微粒群算法进行了求解[13]。

除了针对传统的工期、成本、质量等目标进行优化，文献[14]还考虑了工程项目实际中风险(安全)、资源以及效益、环境等影响因素并建立了相应的模型进行求解，但有关此类的研究较少，更多的学者试图改进TCT(time-cost trade-off)问题和TCQT(time-cost-quality trade-off)问题中工期、成本和质量关系的假设，进行不确定条件下工程项目的多目标优化问题的研究。

3 不确定条件下的多目标均衡优化

3.1 多模式均衡优化模型

Vanhoucke M等在其研究中将多模式的工期－成本多目标优化问题分为3种类型:“截止日期型”、“预算确定型”以及“寻优曲线型”，且被广大的学者接受认可[15]。Peng W L和 Wang C G结合多模式资源受限的工程项目多目标优化问题的特点，在考虑项目可再生资源的基础上建立了工期－成本的均衡优化模型，并结合“截止日期型”具体工程实例给出了工程项目工期－成本的均衡优化曲线[16]。Zhang J W和Shan H F在Peng W L和Wang C G的基础上将与再生资源相关的成本纳入可再生资源的范畴之内，建立了两类多模式的资源受限的工期－成本均衡优化模型[16，17]。

ElRayes K和Kandil A提出了考虑时间、成本、质量3个目标的多模式均衡优化模型，学者假设工序的质量、成本、工期由建造方法、工人数量、工人加班3个因素决定，3种因素的不同搭配形成了不同的工序施工方案。在此基础上，学者根据各因素的权重和各工序的权重进行加权平均得到整个项目的质量水平[18]。该研究为多模式的工程项目多目标优化模型的构建提供了较好地借鉴。Afshar A等在前人的基础上建立了更为简洁的多模式工期－成本－质量多目标均衡优化模型，通过对工序质量表征因子的得分进行加权得到工序的质量水平

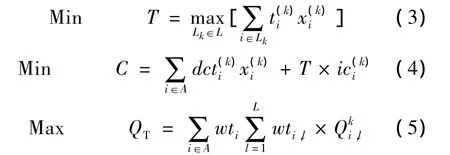
式中，T、C、QT为工程项目总的工期、成本和质量;、为项目工序i采用第k种执行模式时的持续时间和成本;为工序采用第k种执行模式时第l个质量表征因子的质量水平;为是否采用第k种执行模式，即当采用第k种执行模式时，=1，相反为0;表示工序i采用第k种执行模式时该工序的直接成本;表示工序i采用第k种执行模式时该工序间接成本率[19]。Rahimi M和Iranmanesh H建立了离散的工程项目工期成本质量优化模型并将离散变量连续化以适应微粒群算法的特点进行求解[20]。

以上多模式的工期－成本－质量均衡优化模型均考虑了工程的项目实施过程中的实际影响因素，增加了模型的实际应用价值。值得指出的是，对工期成本以及工期－质量之间的线性关系的假设不能很好地反映工程项目实际，另外以上的优化模型大多仅考虑了工期与质量之间的关系，较少考虑到成本对质量的影响。

3.2 多目标模糊均衡优化模型

项目实施过程中的很多不确定因素都会对项目工期造成影响，这使得项目成本、质量随着项目工期的波动处于动态变动中，计划评审与审查技术、概率网络评审技术和蒙特卡罗模拟方法通过将工期、成本模糊化来反映实际工程目标变量的不确定性是较为经典的模糊优化方法。除此以外，学者们提出了利用模糊集来反映工程项目网络计划中的不确定因素的方法，通过隶属度函数表示工程项目的工期、成本和质量，并进行模糊运算从而构建出多目标模糊均衡优化模型。该类模型多适用于项目的历史信息较少的情况，此时专家可以根据自身的经验利用模糊理论中的隶属度函数更好地对项目各项参数进行估计。Mokhtari H等基于PERT(program evaluation and review technique)网络建立了多模式的项目成本的离散函数并假定项目工期呈正态分布，建立了模糊的离散的工期成本均衡优化模型，并首次利用蚁群算法得到了模型的优化结果[21]。Hapke M 等[22]利用模拟退火算法来解决多目标模糊资源受限的项目调度问题。但是模型只考虑了直接成本，没有考虑整个项目的全部成本。

3.3 多目标随机均衡优化模型

多目标随机均衡优化模型将环境的不确定性考虑到模型的构建中，通过确定工程工期和成本的概率分布函数来研究动态环境中的工期－成本优化问题，常利用平均值准则进行决策。与传统的工期－成本优化模型相比，这种建模方法更接近实际。但是随机模型对项目工期成本概率分布的模拟是建立在大量已有数据的基础上的，所以随机模型对于有大量历史数据的项目而言表现更优。Freeman R J最早研究了环境的不确定性并将其纳入工程项目优化模型的构建[23]，此后的学者在工程项目优化的研究中也考虑了环境的不确定性这一因素[24]，但早期的随机均衡优化模型的构建常常是将决策变量离散化，而实际问题的数量级往往较大，离散模型的实用性往往受到一定的限制。

Feng C W等在其确定条件下的工期－成本均衡模型[2]的基础上，运用模拟技术构建了动态随机环境下的工程项目工期－成本优化模型，将解集中的最小平均距离作为凸集的适应度函数，并运用改进的遗传算法对模型进行了求解[25]。Zheng D X M等结合模糊集理论对工程项目的工期、成本指标进行描述建立了工程项目的多目标优化模型[26]。Zheng D X M等引入经济学中的效用理论、机会成本理论来模拟人们的实际决策过程，得到了不同风险水平下工期－成本的最优组合[26]。

Ke H等、Aghaie A和Mokhtari H利用随机变量构建了随机条件下的工程项目工期－成本均衡优化模型，打破了前人只是在完工期内寻求最短工期的目标，引入了新的决策准则——在规定完工期内完工可能性最大，并对模型进行了构建和求解[27，28]。Ke H等在新的准则下建立了可能性受限规划模型和相依可能性规划模型，并将随机模拟和遗传算法相结合对模型进行了求解，该文献结合项目实例分别在不同的决策准则下对模型进行了求解[27]。Aghaie A和Mokhtari H假定工程项目的成本离散且服从指数分布，用蒙特卡罗模拟技术应用关键路径法找到了网络中的关键路径，在被选择的关键工序上建立了非线性整数规划模型，应用蚁群算法对模型进行了求解[28]。

3.4 多目标鲁棒均衡优化模型

尽管多目标随机均衡优化模型的实用性相比经典的工程项目优化模型有了很大改进，但这类模型在实际应用中的表现并不尽如人意。首先，随机型的优化模型需要考虑不确定因素的随机分布规律，但是这对于充满不确定性的实际工程来说是很困难的，尤其是随着社会的发展，工程项目的特殊性越来越强，针对大型复杂项目而言，项目的历史数据很难获得;其次，即便模型能够大致模拟出实际变量的分布规律，但是因环境的微小扰动而导致优化结果受到影响的情况是很常见的，此时解的最优性受到很大影响，往往连次优或者近似最优都不能达到。而且目前随机均衡优化模型大多利用平均值准则进行决策，但是实际中问题的实现是随机的，这一均值准则对于项目实际的指导意义并不大。而对于多目标模糊均衡优化模型而言，其隶属度函数的确定是较为困难的，尽管学者们提出了不同类型的隶属度函数来描述项目工期、成本的变化规律，但是有关该函数准确性和客观性的论证却几乎不存在。在这种情况下，鲁棒优化模型逐渐受到专家和学者们的青睐并被引入到工程项目工期、成本的均衡优化研究中。鲁棒优化即建立一种性能表现稳定良好的模型，该模型即使在最坏情况发生的条件下也能找到较好的解。

一些学者试图在传统调度模型的基础上寻求模型的鲁棒解。Herroelen W和Leus R研究了工程项目管理资源调度模型的鲁棒性，构建了资源调度线性规划模型并利用启发式算法得到了模型的鲁棒解，当施工过程中单个工序因受到环境扰动而导致工期增加时，该模型解的最优性不会受影响[29]。Lambrechts O等研究了项目中资源可获取性的不确定性，将鲁棒调度方法和改进的反应式调度方法相结合对模型进行了求解[30]。

工程项目多目标鲁棒优化模型的研究近几年才刚刚起步。Cohen I等建立了随机工期－成本均衡优化问题的线性规划模型，并基于鲁棒优化原理将该模型转化成相应的鲁棒优化模型，通过假定工序间隔时间不确定性，来反映实际工程中环境扰动所造成的影响[31]。该文献改进了原有计算方法。模型旨在帮助项目经理仅通过少量已发生的项目进度数据对后续工程项目的实施做出优化的决策，模型能够保证指导原则的鲁棒性。Hazir O等针对离散的工程项目工期成本均衡的鲁棒优化问题进行了研究，建立了3个鲁棒优化模型，通过项目成本的不确定性表征环境所造成的扰动，并假定工序间隔时间可以通过工序的执行模式来确定[32]。该模型首次将鲁棒优化应用到离散的工期－成本均衡优化问题中，为离散的工程项目工期成本鲁棒优化模型的研究奠定了较好的基础。

鲁棒优化在工程项目多目标均衡优化方面的应用处于刚刚起步的阶段，针对实际环境的不确定性，学者们一方面基于传统的优化模型寻求具有鲁棒性的解，另一方面通过应用鲁棒优化的方法将实际环境的不确定性考虑到模型的构建中，建立对环境扰动不敏感的鲁棒优化模型，提高其实际应用性。多目标模糊优化模型、多目标随机优化模型以及多目标鲁棒优化模型都是解决客观环境不确定性的动态处理方法，近年来的研究尚处于探索阶段，但模型的实用价值较高，研究的潜力较大。

4 结语

本文在文献研究的基础上，分别对确定条件下和不确定条件下工程项目多目标优化问题的研究进行了综述。针对不同学者建立的工程项目多目标优化模型进行了总结分析，并展望了该问题的未来研究趋势和方向。有关确定型的工程项目多目标均衡优化问题的研究，学者们就项目工期－成本之间的关系已有较为一致的认识，但有关项目的质量目前存在着多种量化方法，尚未确定最优的定量方法，有关问题还需要进一步研究。相比确定条件下的工程项目工期成本质量均衡优化问题，不确定条件下的模型更为复杂，由于该类型问题的研究尚处于起步阶段，大多数的优化模型仅考虑了工期和成本两个目标，如何将工程质量、安全等因素纳入模型的构建有待进一步研究。

在本文所综述的文献中，大多数研究局限于模型的构建和算法的改进，只有少数学者考虑了实际项目的决策过程对多目标优化决策支持系统进行开发，用以辅助项目管理者的决策[2]。对于项目管理者来说，在得到的工程项目多目标Pareto解集中寻找适合自身需求的解依然是较为困难的，如何基于项目管理者的不同偏好在众多Pareto解中进行决策选择是目前工程项目多目标优化与决策研究的一个重要方面。总之，智能优化算法在工程项目多目标优化领域的应用前景是广阔的，随着智能优化算法在工程项目多目标优化问题上的进一步发展，其解决问题的效率和准确度都将进一步加强，从而提供更具指导性的优化方案，进一步满足实际需求。

[1]Kelley JE. The criticalpath method:Resources planning and scheduling[J].Industrial Scheduling，1963:347 －365.

[2]Feng C W.Using genetic algorithms to solve construction timecost tradeoff problems[J].Journal of Computing in Civil Engineering，1997，11:184－189.

[3]Babu A J G，Suresh N.Project management with time，cost，and quality considerations [J].Journal of Operational Research，1996，88:320－327.

[4]Brucker P，Drexl A，Mohring R，et al.Resourceconstrained project scheduling:Notation，classification，models，and methods[J].European Journal of Operational Research，1999，112(1):3－41.

[5]李红仙，宣卫红，谈 飞，等.基于激励遗传算法的动态时间/费用优化[J].系统工程学报，2007，22(3):333－336.

[6]Li H，Love P.Using improved genetic algorithms to facilitate timecost optimization[J].Journal of Construction Engineering and management，1997，123:233 －237.

[7]Li H，Cao J N，Love P.Using machine learning and GA to solve timecost tradeoff problems[J].Journal of Construction Engineering and Management，1999，125:347 －353.

[8]Zheng D X M，Ng S T，Kumaraswamy M M.Applying Pareto ranking and niche formation to genetic algorithmbased multiobjective timecost optimization[J].Journal of Construction Engineering and Management，2005，131(1):81 －91.

[9]Xiong Y，Kuang Y.Applying an ant colony optimization algorithmbased multiobjective approach for time-cost tradeoff[J].Journal of Construction Engineering and Management，2008，134(2):153－156.

[10]Yang I.Using elitist particle swarm optimization to facilitate bicriterion timecost tradeoff analysis.[J].Journal of Construction Engineering and Management，2007，133(7):498 －505.

[11]Zheng D X M，Ng S T，Kumaraswamy M M.Applying Pareto ranking and niche formation to genetic algorithmbased multiobjective time-cost optimization[J].Journal of Construction Engineering and Management，2005，131:81 －91.

[12]Khang D B，Myint Y M.Time，cost and quanlity tradeoff in project management:a case study[J].International Journal of Project and Management，1999，17(4):249 －256.

[13]陈勇强，高 明，张连营.基于遗传算法和Pareto排序的工期费用质量权衡模型[J].系统工程理论与实践，2010，30(10):1774－1780.

[14]ElRayes K，Khalafallah A.Tradeoff between safety and cost in planning construction site layouts[J].Journal of construction engineering and management，2005，131:1186 －1195.

[15]Vanhoucke M，Demeulemeester E，Herroelen W.Discrete time/cost tradeoffs in project scheduling with timeswitch constraints[J].Journal of the Operational Research Society，2002:741 －751.

[16]Peng W L，Wang C G.A multimode resource-constrained discrete time-cost tradeoff problem and its genetic algorithm based solution [J].International Journal of Project Management，2009，27(6):600－609.

[17]Zhang J W，Shan H F.Multi-mode double resource-constrained time/cost trade-offs project scheduling problems[C]//International Conference on Management and Service Science.Wuhan:MASS，2009:1－4.

[18]ElRayes K，Kandil A.Timecostquality tradeoff analysis for highway construction[J].Journal of Construction Engineering and Management，2005，131:477 －486.

[19]Afshar A，Kaveh A，Shoghli O R.Multiobjective optimization of timecostquality using multicolony ant algorithm[J].Asian Journal of Civil Engineering(Building And Housing)，2007，8(2):113－124.

[20]Rahimi M，Iranmanesh H.Multi objective particle swarm optimization for a discrete time，cost and quality tradeoff problem[J].World Applied Sciences Journal，2008，4(2):270 －276.

[21]Mokhtari H，Baradaran Kazemzadeh R，Salmasnia A.Time-cost tradeoff analysis in project management:An ant system approach[J].Engineering Management，IEEE Transactions on，2011，58(1):36－43.

[22]Hapke M，Jaszkiewicz A，Sowinski R.Pareto simulated annealing for fuzzy multiobjective combinatorial optimization[J].Journal of Heuristics，2000，6(3):329－345.

[23]Freeman R J.A generalized network approach to project activity sequencing [J].Engineering Management，IRE Transactions on，1960(3):103－107.

[24]Charnes A，Cooper W W，Thompson G L.Critical path analyses via chance constrained and stochastic programming[J].Operations Research，1964:460－470.

[25]Feng C W，Liu L，Burns S A.Stochastic construction timecost tradeoff analysis[J].Journal of Computing in Civil Engineering，2000，14(2):117 －126.

[26]Zheng D X M，Ng S T.Stochastic time-cost optimization model incorporating fuzzy sets theory and nonreplaceable front[J].Journal of Construction Engineering and Management，2005，131(2):176－186.

[27]Ke H，Ma W，Ni Y.Optimization models and a GAbased algorithm for stochastic timecost tradeoff problem[J].Applied Math-ematics and Computation，2009，215(1):308－313.

[28]Aghaie A，Mokhtari H.Ant colony optimization algorithm for stochastic project crashing problem in PERT networks using MC simulation[J].The International Journal of Advanced Manufacturing Technology，2009，45(11):1051－1067.

[29]Herroelen W，Leus R.The construction of stable project baseline schedules[J].European Journal of Operational Research，2004，156(3):550－565.

[30]Lambrechts O，Demeulemeester E，Herroelen W.Proactive and reactive strategies for resourceconstrained project scheduling with uncertain resource availabilities [J].Journal of Scheduling，2008，11(2):121－136.

[31]Cohen I，Golany B，Shtub A.The stochastic time-cost tradeoff problem:A robust optimization approach [J].Networks，2007，49(2):175－188.

[32]Hazir O，Erel E，Gunalay Y.Robust optimization models for the discrete time/cost tradeoff problem[J].International Journal of Production Economics，2011，130:87 －95.