面向健康诊断的混凝土斜拉桥模型设计与分析

张国刚，方 志，唐盛华，陈素君，陈 峰

(1.湖南大学土木工程学院，长沙 410082;2.惠州市公用事业管理局，广东惠州 516001)

1 前言

目前，基于数值模拟的损伤识别研究对于实际复杂的工程结构还存在较大的局限性，而实际结构上通常不允许进行损伤试验，因此，以结构模型试验为手段的结构损伤识别研究就显得尤为重要。

迄今为止，已有部分学者对桥梁结构模型设计及损伤识别试验研究进行了一些研究和探索。铁道部大桥局桥科院完成了多座不同类型桥梁结构的模型试验，刘自明[1]详细介绍了模型试验研究在模型设计、制造、安装和选用材料方面所应注意的问题;颜东煌、田仲初等[2，3]采用铝合金材料制作了洞庭湖大桥相似模型(1∶30)，对斜拉桥静动力相似关系进行了研究，从理论上提出采用刚度相似法来处理斜拉桥模型设计中弹性模量相似比不一致的问题;赵翔等[4]通过润扬斜拉桥模型试验进行了传感器优化布置研究及拉索损伤对斜拉桥静动力性能的影响研究;孙宗光等[5]以构想的一座长1 000 m的悬索桥为原型，设计制作了1∶100的缩尺模型，并对其进行了静载试验和损伤模拟试验，探讨了悬索桥的主要受力变化规律和灵敏度特性;项贻强等[6]基于刚度相似原理设计了一座PC斜拉桥的理想模型桥，将其与实桥有限元数值模拟及原型成桥试验结果进行了比较分析。

对于大型桥梁结构，模型试验研究主要是针对设计和施工的，针对健康监测损伤识别的研究较少，斜拉桥模型的设计材料主要选取的是铝合金材料和有机玻璃材料，未见采用混凝土材料，无法准确模拟混凝土斜拉桥结构的损伤。本文以广东惠州合生大桥为原型，设计并制作了一座1∶15的大比例混凝土斜拉桥模型，该模型主要用于损伤识别试验研究。文中对混凝土斜拉桥模型设计制作需要着重考虑的问题进行了阐述，并给出了解决办法。

2 面向健康诊断的混凝土斜拉桥模型设计

2.1 原型桥概况

广东惠州合生大桥主桥(以下简称原型桥)为独塔双索面预应力混凝土斜拉桥，该桥总长326 m，宽35.5 m，桥跨布置为180 m+101 m+45 m;设计荷载为公路I级;全桥共布设了108根斜拉索，梁上标准索距6 m，塔上标准索距1.8 m;主梁采用Π形截面，梁高 2.3 m，桥面板厚度 0.32 m;主塔高121 m，两塔桥面以上无横撑，总体布置如图1所示。

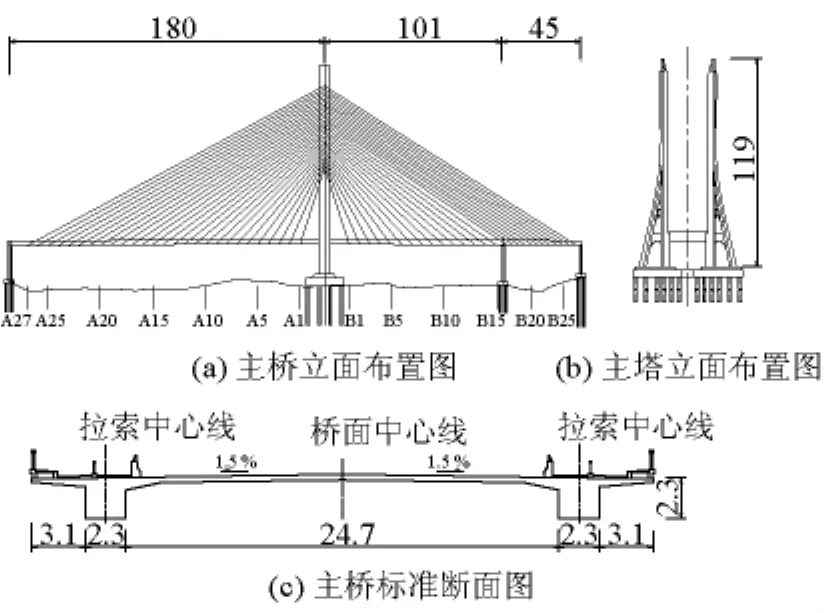
图1 合生大桥总体布置(单位:m)Fig.1 Overall layout of the Hesheng Bridge(unit:m)

2.2 模型设计

结构模型设计首先应根据相似理论确定模型和原型的相似关系。这些相似关系主要包括几何相似、物理相似和边界条件相似[7]。对于全几何相似的模型，常用的相似关系如表1所示。

表1 结构模型设计常用相似关系表Table 1 Similarity used in structure model design

模型设计时首先要考虑的问题是几何缩尺比的确定和模型材料的选择。本模型试验的目的主要是对混凝土斜拉桥进行损伤识别研究，因此，为了能够模拟混凝土结构的损伤特性，模型制作的材料应选择混凝土材料，即cE=1，而根据混凝土构件的制作条件和试验场地的大小可知，几何缩尺比应选择较大的值，本模型几何缩尺比确定为c=，至此，l可根据表1相似关系确定模型与原型各物理量的相似比。

根据表1中相似比及原型桥的结构参数可以确定模型桥的设计尺寸及相应的物理参数，此时的模型桥可称为理想模型桥，其静动力特性与原型桥完全满足相似理论，但是在实际模型设计制作中，常因模型制作困难、材料限制、加载限制等问题，理想模型桥在现实中实现非常困难。例如，按相似关系，模型桥桥面板厚度仅为2.13 cm，采用混凝土材料制作难度大;另外按照质量密度ρ的相似关系，模型桥材料质量密度应为原型桥材料密度的15倍，而这种材料很难找到，一般采用配重的方法来近似模拟，模型桥仅主梁配重约1 000 kN，此配重数量巨大，费用高，较难实现，而且主塔和拉索的配重施加难度更大。

可见，模型设计过程中有很多问题需要解决，需要按照试验目的的要求充分考虑，使模型在保证主要参数相似的同时，忽略某些次要物理量的相似关系，同样可以达到试验的预期目的，并且避开了实际模型设计的困难。建立原型桥和理想模型桥的有限元模型，用于在解决相关问题时调整某些参数对原型和模型相似性的影响进行分析。

本模型设计应考虑并解决以下几个关键问题。

1)模型配重难度大，费用高。配重的主要作用是使模型桥成桥状态的应变与原型桥满足相似关系，而本试验不对成桥状态进行深入讨论，因此，本模型桥设计省略配重。通过对理想模型桥有限元模型进行修改分析可见，不配重不影响模型的刚度，模型的静力性能增量仍然满足相似关系，但改变了模型桥的质量特性，对动力性能影响较大，即相似比变为c=1，c=，可见模型桥和原型桥动力特性ρf仍然相似。

2)混凝土构件制作限制，几何相似难以保证。斜拉桥结构主梁和主塔的抗弯刚度是影响斜拉桥静动力特性的敏感参数，因此，对于模型桥主梁和主塔应主要满足抗弯刚度相似，在满足制作条件的前提下，放松对轴向刚度和扭转刚度等参数的相似要求。因此，需对主梁和主塔的截面尺寸进行重新设计，为简化制作和施工，主梁和主塔各采用同一截面形式，并简化细部构造。对理想模型桥有限元模型进行修改后分析，原型和模型静力位移增量相似比如图2所示，各阶频率相似比如图3所示。

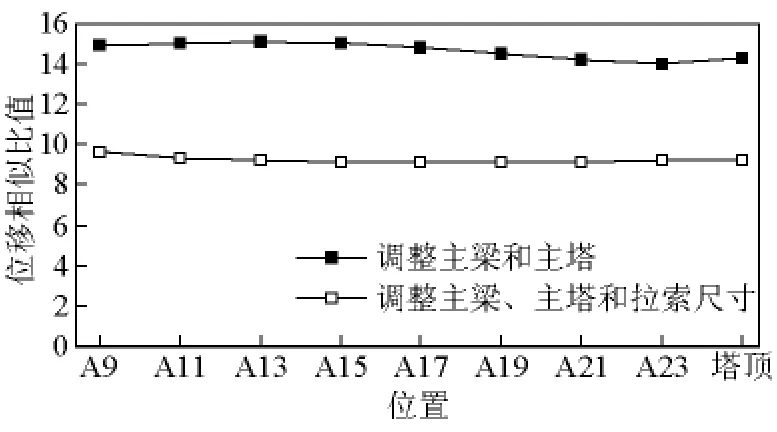
图2 静力位移增量相似比值Fig.2 Similar ratio of static displacement increment

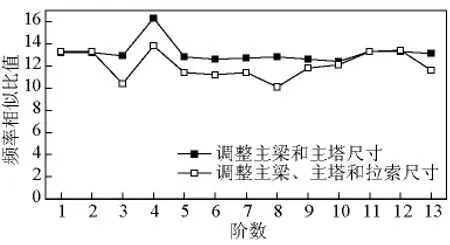
图3 各阶频率相似比值Fig.3 Similar ratio of frequencies

由图2和图3可见，调整主梁和主塔尺寸后的模型与原型静力位移仍保持良好的相似性;频率相似比由原来的15降低为13左右，这是因为模型主梁和主塔截面尺寸的调整改变了其质量相似特性，调整后的主梁和主塔换算密度 cρ=1.3，则 cf=，与有限元计算相符，而第4阶主梁扭转频率相似比与其他各阶相似比差别较大，这是因为模型桥面板厚度增大，导致主梁扭转惯性矩增大，进而导致扭转频率相似比变大。

3)拉索体系的简化。模型桥若按实桥布索，主梁上拉索间距仅40 cm，索塔上的间距仅12 cm，使拉索的安装、张拉、锚固都很困难，索力调整的工作量也很大。本设计将拉索根数减半，即将实桥中编号为偶数的拉索去掉，将其等效到相邻的拉索中去。由于模型拉索规格较多、数量少、采购困难，另外还需加工较多的复杂连接件，因此，为简化拉索连接构造，拉索统一选用单根直径为7 mm的高强钢丝。拉索理论直径如表2所示。

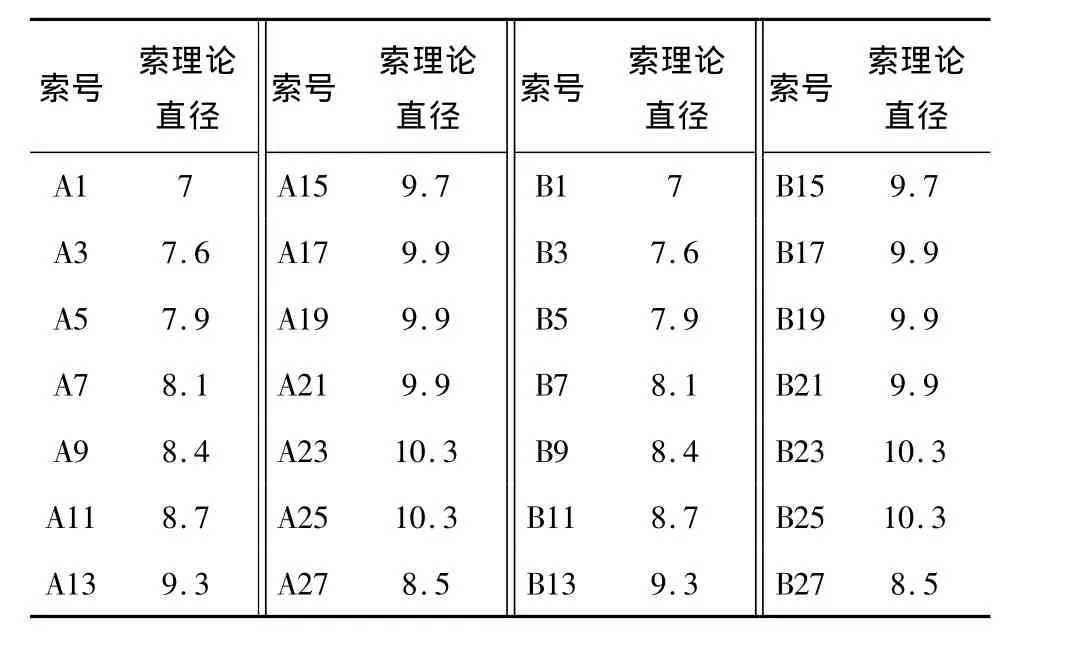
表2 模型桥拉索理论直径表(单位:mm)Table 2 Cable theory diameter of model bridge(unit:mm)

模型桥实际拉索面积较理论值减少50%左右，拉索刚度降低对模型桥的静动力特性产生了较大影响，静力位移增量相似比由原来的15降低为9.1左右，但仍保持良好的相似性;拉索刚度降低对主塔横向弯曲模态频率(如第1、2、11和12阶)影响很小，对主梁竖弯及主塔纵向弯曲模态频率影响较大，但未见模态丢失或变异，模型桥动力特性仍能反映原型桥的模态特性。

以上对模型设计中的几个关键问题进行了处理，通过分析可见，模型桥静动力特性与原型桥仍然保持较好的相似性，并且避开了模型设计中的困难。因此，上述处理方法可行。按照上述方法设计并制作了模型桥，模型桥总体布置如图4所示，建成的模型桥如图5所示。

图4 模型桥总体布置(单位:mm)Fig.4 Overall layout of the model bridge(unit:mm)

图5 模型桥成桥状态Fig.5 Finished state of the model bridge

3 原型桥和模型桥有限元建模与模型修正

建立原型桥初始有限元模型，依据实测数据对其进行修正得到该桥的基准有限元模型。同时建立模型桥初始有限元模型，对模型桥进行静动力测试，依据实测数据对其进行修正得到模型桥基准有限元模型。

3.1 原型桥有限元建模与模型修正

原型桥计算模型采用“鱼骨”模式[8]，主梁、主塔和桥墩采用空间梁单元模拟，斜拉索采用空间杆单元模拟，主梁与斜拉索的联系采用刚性梁单元模拟。支座的模拟通过耦合模型中相应节点自由度的方法来实现，塔梁墩固结，桥墩在承台处按固结处理。原型桥有限元模型如图6所示。

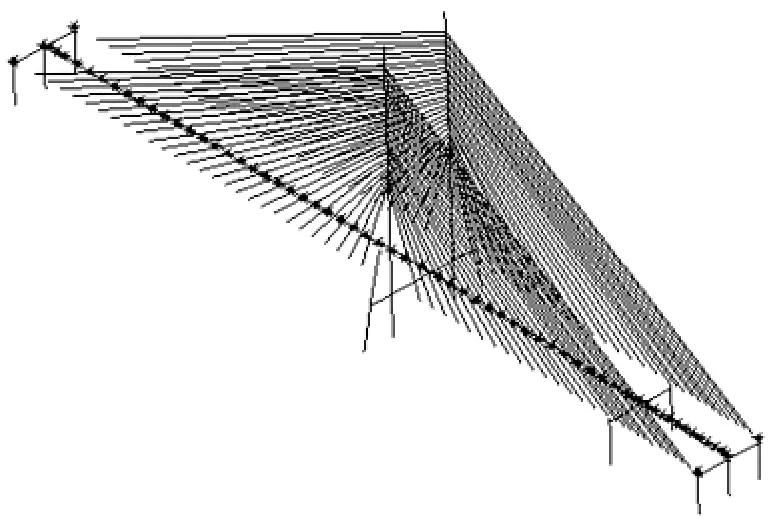
图6 原型桥有限元模型Fig.6 Finite element model of prototype bridge

以实测结果为依据，以有限元模型物理参数为修正变量，理论与实测频率的误差平方和为目标函数，采用基于灵敏度分析的模型修正技术[9]对初始有限元模型进行修正，模型修正的结果对比如表3所示，计算频率误差对比如图7所示。可见，模型修正后计算频率与实测值的最大误差为3.14%，频率误差明显减小，说明修正效果良好，修正后的有限元模型能够较好地模拟实际结构，可作为基准有限元模型。

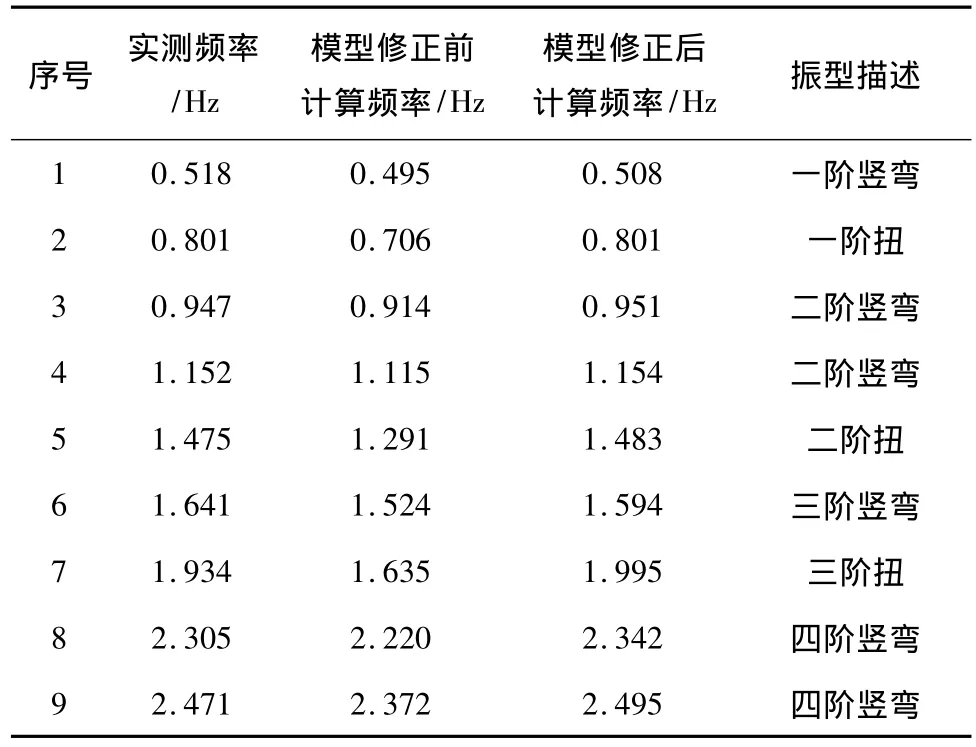
表3 原型桥模型修正前后有限元计算频率和实测值比较Table 3 Comparison of prototype bridge FEM calculatingand test results before and after model updating

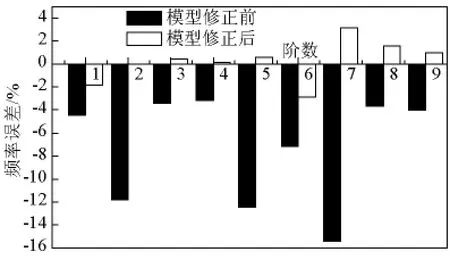
图7 原型桥模型修正前后计算频率误差对比图Fig.7 Frequency error comparison of prototype bridge FEM before and after model updating

3.2 模型桥有限元建模与模型修正

模型桥计算模型采用梁壳模型[10]。将Π形主梁分成三部分，桥面板和两侧Π脚，桥面板采用壳单元模拟，两侧Π脚采用梁单元模拟，壳单元和梁单元之间节点采用刚臂连接。主塔采用梁单元模拟，斜拉索采用杆单元模拟，横梁采用梁单元模拟，拉索和主梁的连接采用刚臂连接。桥墩和桥塔基础按固结处理。模型桥有限元模型如图8所示。

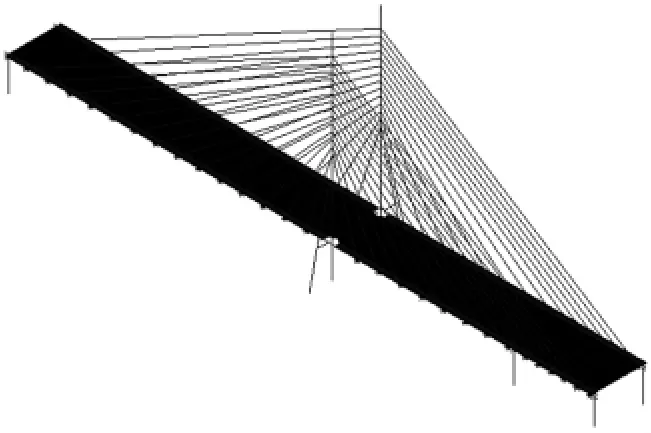
图8 模型桥有限元模型Fig.8 Finite element model of model bridge

以实测结果为依据，采用与原型桥相同的模型修正方法对模型桥初始有限元模型进行修正，模型修正前后的结果对比如表4所示，计算频率误差对比如图9所示。可见，模型修正后计算频率与实测值的最大误差为1.64%，频率误差明显减小，说明修正效果良好，修正后的有限元模型能够较好地模拟实际结构，可作为后续斜拉桥损伤识别研究的基准有限元模型。

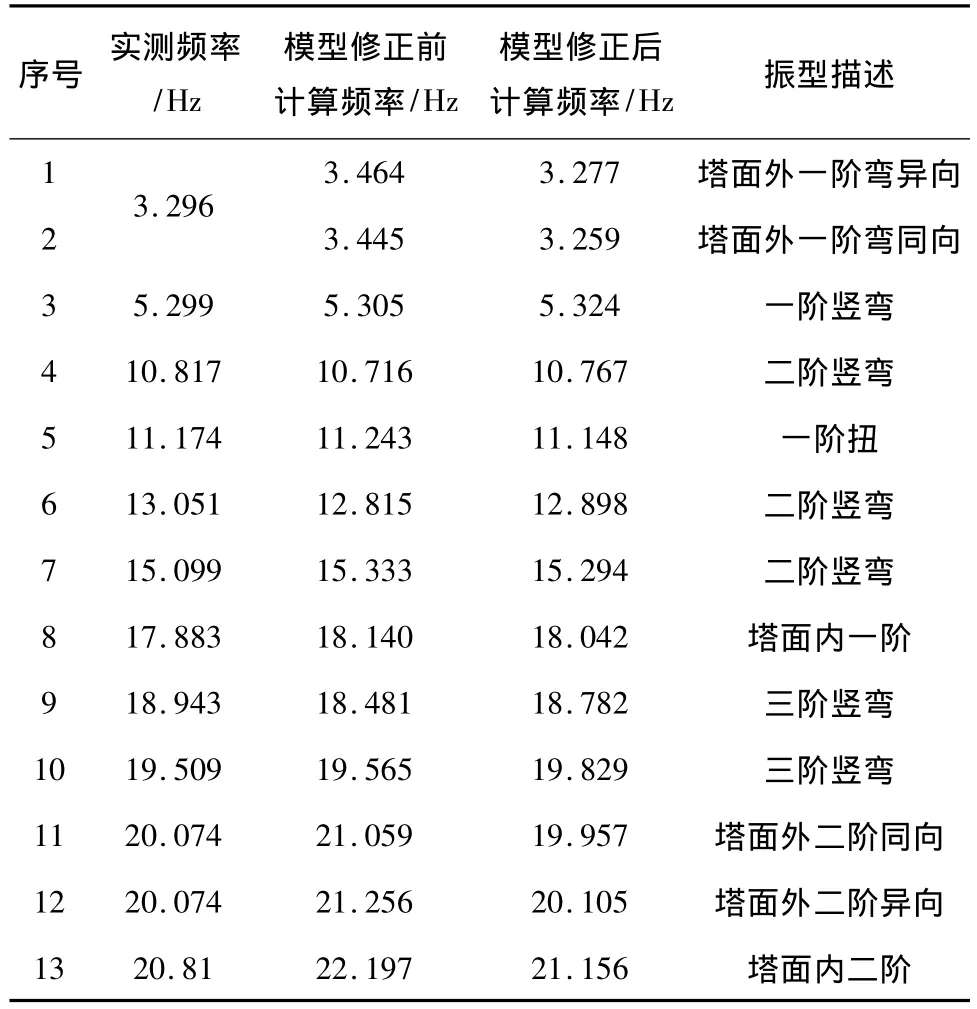
表4 模型桥模型修正前后有限元计算频率和实测值比较Table 4 Comparison of model bridge FEM calculatingand test results before and after model updating

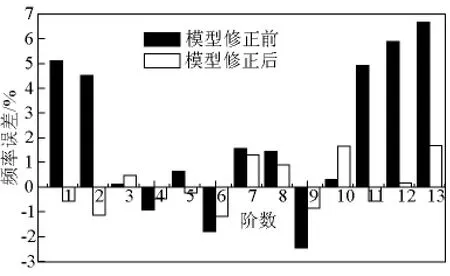
图9 模型桥模型修正前后计算频率误差对比图Fig.9 Frequency error comparison of model bridge FEM before and after model updating

4 完好状态下原型桥和模型桥静动力特性相似性分析

采用上节的基准有限元模型对原型桥和模型桥进行静动力特性分析，将原型桥和模型桥的静动力特性进行对比，考察其相似性。

4.1 静力相似性分析

分析模型桥在荷载作用下主梁和主塔的位移，以考察其与原型桥的静力相似性。在模型桥主梁上施加5 kN/m的均布荷载，按照表1的相似关系，应在原型桥主梁上施加75 kN/m的均布荷载，模型桥和原型桥在荷载作用下的静力位移比较如表5所示。

表5 模型桥与原型桥静力位移比较Table 5 Static displacement comparison of model bridge and prototype bridge

由表5可见，模型桥与原型桥主跨跨中附近及塔顶位移比值均为9.1左右，而按照表1相似关系，位移理论比值应为15，这是由于模型桥拉索简化刚度降低引起的，模型桥主梁下挠较大，位移比值降低，但模型桥和原型桥静力位移仍满足一定的相似性。

4.2 动力相似性分析

模型桥和原型桥动力特性比较如表6所示，模型桥和原型桥的模态相似性通过MAC值来体现，MAC值越接近于1表示相似性越好，MAC值越接近于0表示模态相似性越差。MAC值的计算见式(1)。

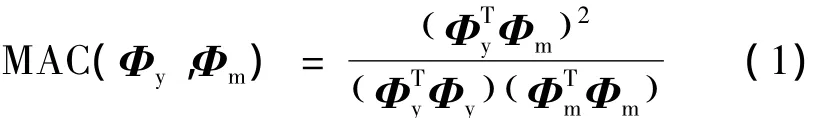
式(1)中，Φy、Φm分别为原型桥和模型桥的模态列向量。

由表6可见，模型桥与原型桥主梁和主塔弯曲频率比值均较接近，比值在10～12之间，模型桥和原型桥固有振型具有良好的相似性，主梁扭转频率比值较大，而按照表1相似关系，忽略配重影响之后，模型桥与原型桥频率理论比值应为15，但由于拉索面积的简化及忽略主梁轴向刚度的影响，导致模型桥频率降低，进而导致了模型桥与原型桥频率比值的降低。模型桥与原型桥振型MAC值均大于0.85，说明模型桥和原型桥固有振型具有良好的相似性。由于模型桥设计忽略了主梁扭转刚度的相似及拉索面的简化导致模型桥主梁扭转频率与原型桥相似性较差。

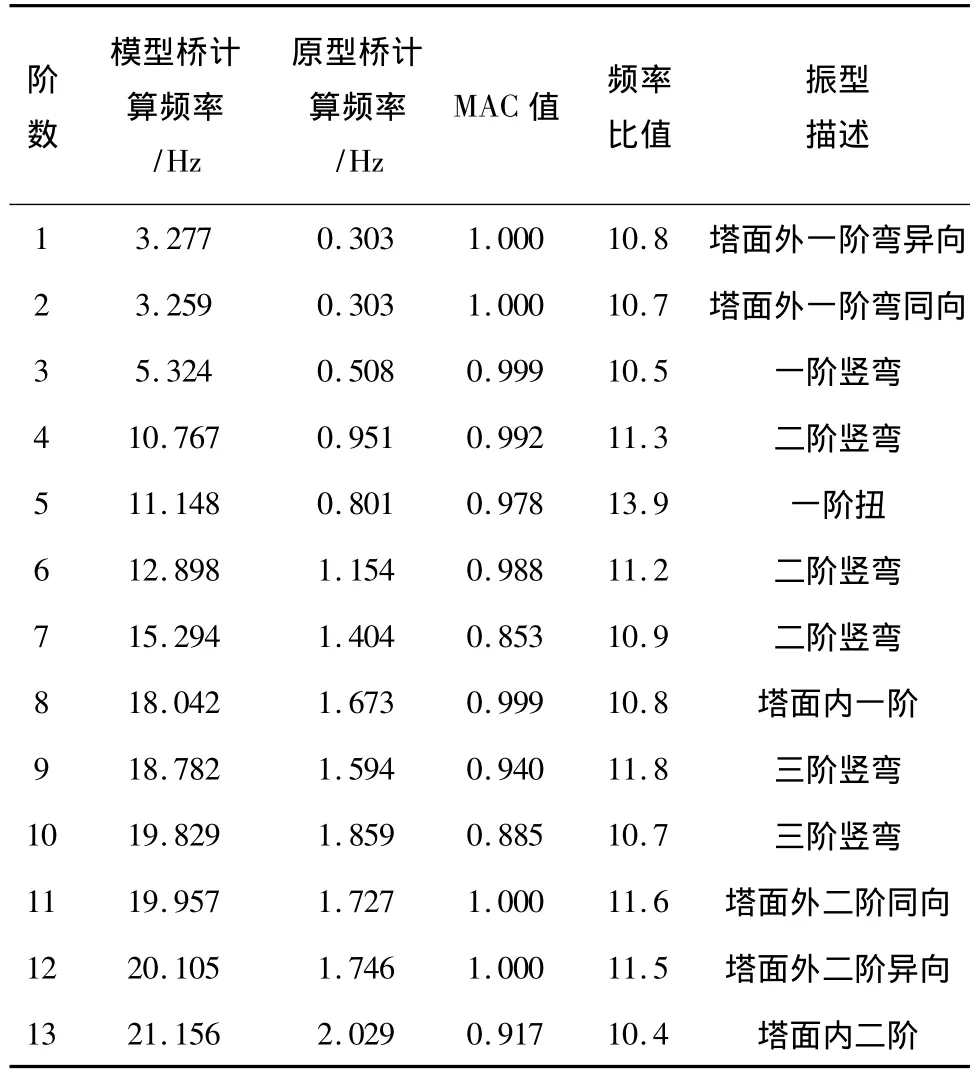
表6 模型桥与原型桥动力特性比较Table 6 Dynamic property comparison of model bridge and prototype bridge

5 损伤状态下静动力相似性分析

采用基准有限元模型对原型桥和模型桥进行损伤数值模拟，考察其损伤相似性。模拟同一位置发生不同程度刚度损伤的情况，损伤位置为主跨A17和A19索之间主梁梁段，损伤程度分别为30%、50%和80%。

5.1 静力损伤相似性分析

分析不同损伤状态下模型桥和原型桥主梁在荷载作用下的位移增量，以考察其静力相似性。荷载与3.1节荷载布置情况相同。模型桥和原型桥不同损伤状态下位移增量如图10、图11所示。A17和A19号索位置位移增量百分比如表7所示。静力位移增量百分比公式见式(2)。

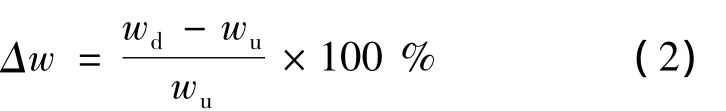
式(2)中，wd、wu分别表示损伤和未损伤状态下的静力位移。

表7 损伤状态下位移增量百分比ΔwTable 7 Comparison of Δw in damage states

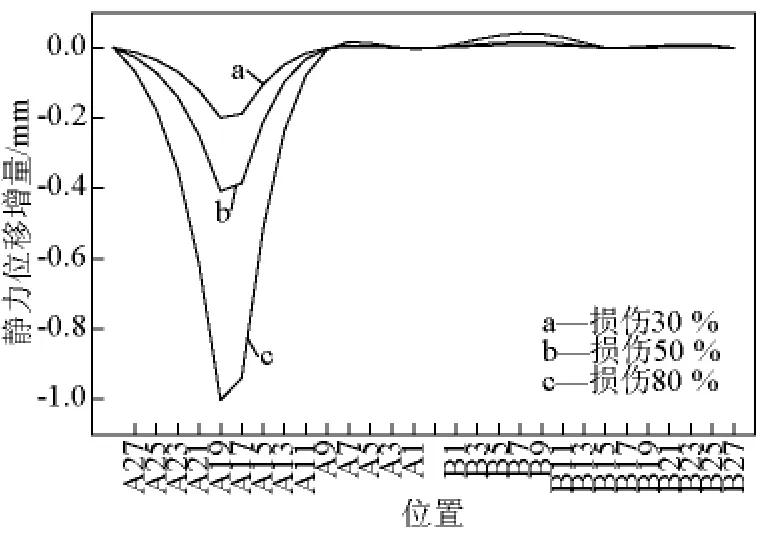
图10 模型桥不同损伤状态下主梁位移增量对比图Fig.10 Displacement increment comparison ofmodel bridge in different damage states

图11 原型桥不同损伤状态下主梁位移增量对比图Fig.11 Displacement increment comparison ofprototype bridge in different damage states

由图10、图11可见，静力位移增量能够较好地识别损伤，模型桥和原型桥具有相似的损伤特性;由表7可见，模型桥和原型桥损伤位置静力位移增量百分比较接近，具有良好的相似性。

5.2 动力损伤相似性分析

分析不同损伤状态下模型桥和原型桥动力损伤指标，以考察其动力相似关系。动力损伤指标为频率变化百分比及柔度矩阵对角元素差[11]。频率变化百分比计算见式(3);柔度矩阵对角元素计算见式(4);柔度矩阵对角元素差计算见式(5)。

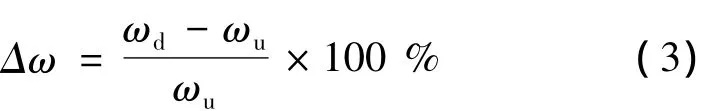
式(3)中，ωd表示损伤状态下的自振频率;ωu表示未损伤状态下的自振频率。

式(4)中，ωr表示第r阶自振频率;φi表示经质量归一化的第r阶振型的第i个分量。

频率变化百分比如图12所示，模型桥和原型桥不同损伤状态下柔度矩阵对角元素增量如图13、图14所示。A17和A19号索位置柔度矩阵对角元素增量百分比对比情况如表8所示。

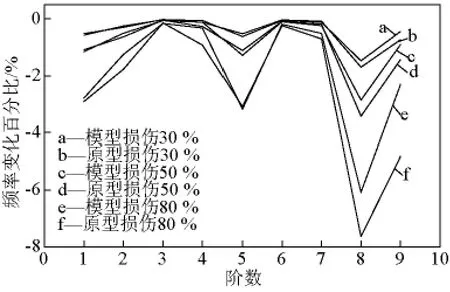
图12 不同损伤状态下频率变化Δω百分比对比图Fig.12 Comparison of Δω in different damage states

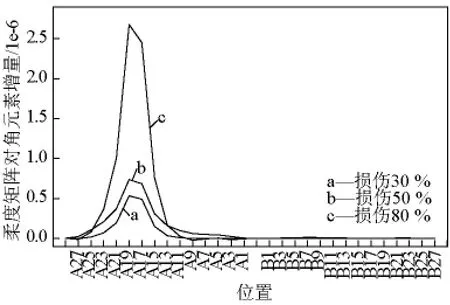
图13 模型桥不同损伤状态下主梁Δfii对比图Fig.13 Δfiicomparison of model bridgein different damage states

图14 原型桥不同损伤状态下主梁Δfii对比图Fig.14 Δfiicomparison of prototype bridgein different damage states

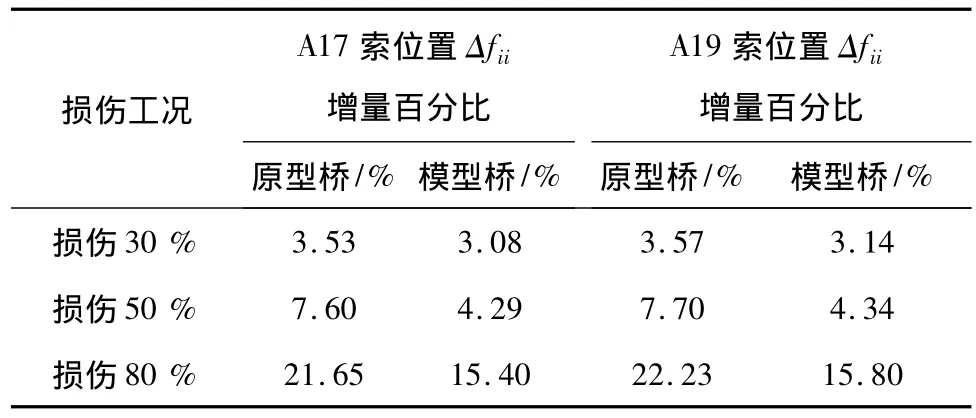
表8 损伤状态下Δfii增量百分比Table 8 Comparison of Δfiiincrement percentage in damage states

由图12可见，不同损伤状态下模型桥和原型桥频率变化百分比具有相似的变化规律，在损伤程度为80%时高阶频率变化百分比相似性较差;由图13、图14可见，柔度矩阵对角元素增量能够较好地识别损伤，模型桥和原型桥具有相似的损伤特性;由表8可见，模型桥和原型桥损伤位置Δfii增量百分比变化规律相似，但随着损伤程度的升高，Δfii增量百分比差别变大。

6 结语

本文基于相似理论对面向健康诊断的混凝土斜拉桥模型设计进行了研究和实践，得出以下主要结论。

1)总结了模型设计过程中的问题并给出了解决办法，采用有限元模型按照所给出的解决办法设计出的模型桥与原型桥静动力性能仍保持一定的相似性，可见所给出的解决办法可行，为混凝土斜拉桥模型设计提供参考。

2)以实测结果为依据对模型桥和原型桥初始有限元模型进行了修正，修正后的有限元模型可作为后续损伤识别研究的基准模型。

3)采用基准有限元模型对模型桥和原型桥的静动力特性及损伤特性进行了相似性分析，分析结果表明模型桥和原型桥的静动力性能及损伤特性仍具有良好的相似性，对该模型桥进行损伤识别试验研究能够较好地反映实际。

[1]刘自明.桥梁结构模型试验研究[J].桥梁建设，1999(4):1－7.

[2]颜东煌，田仲初，陈常松，等.岳阳洞庭湖大桥三塔斜拉桥全桥静动力模型设计[J].长沙交通学院学报，1999，15(1):50－54.

[3]陈常松，颜东煌，田仲初，等.岳阳洞庭湖大桥模型动力相似理论分析[J].桥梁建设，2002(1):48－50.

[4]赵 翔.拉索损伤对斜拉桥结构性能影响的研究[D].南京:东南大学博士论文，2005.

[5]孙宗光，石 健，栗燕娜.面向健康诊断的悬索桥试验模型设计与分析[J].工程力学，2008，25(1):192－195.

[6]项贻强，吴孙尧，段元锋.基于刚度相似原理的斜拉桥模型设计方法[J].实验力学，2010，25(4):438－444.

[7]杨俊杰.相似理论与结构模型试验[M].武汉:武汉理工大学出版社，2005.

[8]Wilson J C ，W Gravelle.Modelling of a cable－stayed bridge for dynamic analysis[J].Earthquake Engineering and Structural Dynamics，1991，20(8):707 －721.

[9]Mottershead J，Friswell M.Model updating in structural dynamics:a survey[J].Journal of Sound and Vibration，1993，167(2):347－375.

[10]方 志，唐盛华，张国刚，等.基于多状态下静动态测试数据的斜拉桥模型修正[J].中国公路学报，2011，24(1):34－41.

[11]Pandey A K，Biswas M.Damage detection in structures using changes in flexibility [J].Journal of Sound and Vibration，1994，169(1):3 －17.