环境监测数据处理与分析

严 晖

(泰兴市环境监测站，泰兴 225400)

环境监测数据处理与分析

严 晖

(泰兴市环境监测站，泰兴 225400)

环境监测是保护环境的重要手段。随着科技发展，监测数据的处理与分析也有了很大的进步，为人类的生活提供了有力的保障。本文从数据获取出发，从多个角度对环境监测数据处理进行分析和研究，同时探讨新型方法在监测数据领域的应用。

环境监测；监测数据；数据融合

1．监测数据获取与可能出现的问题

环境监测是指间断地或连续地测定环境中污染物的浓度，观察、分析其变化和环境影响的过程。在此过程中对影响环境质量的各种因素进行实时或定期采样、分析测量以发现异常的因素，即定期、定点对环境组成、因子和环境中污染物质的种类、浓度、分布的变化及影响进行监测和分析。

环境监测数据具有代表性和完整性，即所获取的检测数据能较全面地描述污染物的空间分布状态。同时还具备准确性和可比性，即数据是经过精密仪器采集，并可通过一定的数据处理方法进行可比性分析验证。

目前监测数据的获取方面存在的问题主要有：数据采集过程中监测人员在数据筛选或处理时出现人为误差；监测点布控没有及时根据附近环境变化而更新布防监控；由于仪器设备过于陈旧而无法进行精密度采集或处理等等。产生以上问题的原因主要有[1]：

（1）主观原因：监测人员本身业务素质较低，并不能将数据进行科学有效的分析和处理，使得部分数据丧失真实性，甚至不能用于评价工作。

（2）客观原因：监测仪器配置和监测站点的布置过于陈旧，并未根据最新环境变化情况更新，使得环境监测数据不具有代表性，造成评价结果的偏差，无法进行科学的分析和处理。

2．分析方法

由于监测数据与污染物空间分布和持续时间等因素有关，故在分析数据时可将数据按周期性规律进行统计分析，从而得出浓度随时间变化的大致规律。同时再根据当地的水文条件、气象变化和地形特征等因素进行综合整理，生成更为详尽的浓度等值线图，便于数据的直观性统计与分析[2]。

2.1 离群数据的分析

环境监测数据获取条件较为复杂，在实际工作中可能由于监测主体或条件变化产生离群值的产生，如何正确区分离群值产生的原因并科学有效地去除离群值，是正确进行评价的重要依据[2]。

2.1.1 Q检验法

在同一组数据中，判断最大值或最小值是否为异常值时采用Q检验法【Dixon(狄克逊)检验法】：将数据从大到小进行排列，根据测定次数进行计算Q值：

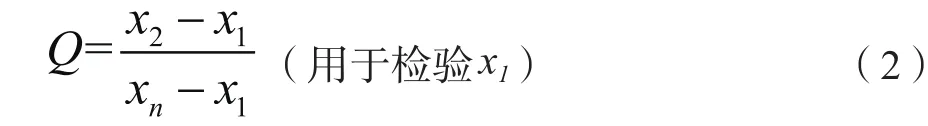
根据测定数据次数n和显著性水平，查Dixon检验统计表, 将Q值与临界值比较, 判断x1与xn是否为离群值：若Q≤Q0.05，则可疑值为正常值；若Q0.05＜Q≤Q0.01，则可疑值为偏离值，可做保留处理；若Q＞Q0.01，则可疑值应予剔除。但该检验方法仅将可疑值与相邻数据进行比较分析，具有一定的局限性[2]。

2.1.2 T检验法

对于各组测定数据平均值的一致性检验可采用( Grubbs)格拉布斯检验法，即T检验法：将监测数据从大到小排列，并计算其算术平均值和标准偏差s，计算T值[2]：

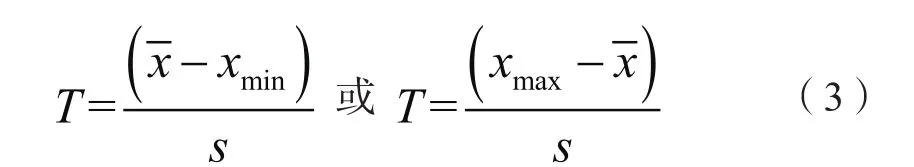
查T检验临界表得T的临界值，若T≥，则可疑数据x1或xn为异常值，应予剔除；反之则采取保留处理。依次反复计算直至无异常数据为止。

2.2 分析结果准确度的检验

2.2.1 平均值与标准值的比较

用于检查监测方法或操作过程是否存在较大系统误差。对标样进行n次监测，再利用T检验法比较监测结果与标准值是否存在显著性差异[2]。

式中： 为标准值，为监测结果，s为标样测定的标准偏差，n为标样测定的次数。根据自由度和置信度P查得T值，与计算结果进行比较。若计算值大于T值，则存在系统误差；若小于则是由偶然误差引起的。环境监测中置信度一般为95%。

2.2.2 两组平均值的比较

针对同一样品的不同组数据产生平均值误差问题，先假设两组数据方差无明显差异（分别为和计算T值[2]：

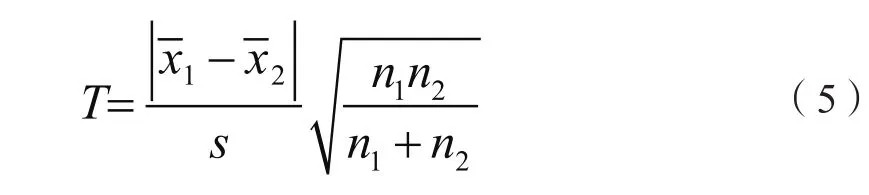
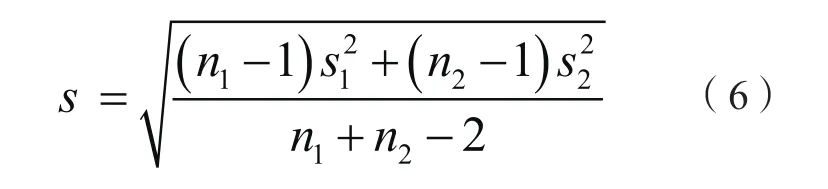
式中：s为合并方差，n为测定次数。用P=95%，=n1+n2-2查表所得T值小于计算值，则存在显著性差异；若大于则无。

2.3 分析结果精密度的检验

用于比较两组数据方差s的一致性，又称F检验：求出两组数据标准方差的平均值和 ，计算

，与F分布表中查得一定自由度下的F值进行比较，若大于计算值则存在显著性差异，若无则不存在。

在进行F检验法检验两组数据的精密度是否有显著性差异时，应先确定其类型：单边检验指一组数据的方差不可能小于另一组数据的方差；而双边检验时，其显著性水平为单边检验时的2倍，置信度变为90%[2]。

2.4 等精度检验

对于n个监测室，用同一标准方法对同一个标准样品作m次监测，测定结果用Cochran最大方差法检验。设各自标准偏差分别为s1，s2，…，sn，最大值记为smax，计算统计量[2]：

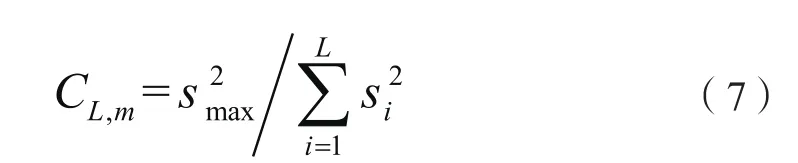
根据给定的显著性水平，实验室个数n，测定次数m，从数理统计表得最大方差检验临界值Ca：C≤C0.05时表明各实验室符合精密度要求；C＞C0.01表明具有最大标准偏差的实验室精密度不符合要求；C0.05＜C≤C0.01表明具有最大标准偏差的实验室精密度具有疑问，需再次考核以确认。

2.5 精密度和准确度统计分析：

2.5.1 标准差分析[2]

(1)对各组数据（x1，y1）分别进行求和Ti、求差Di。将和值用于计算各监测实验室数据分布的标准偏差分母除以2是由于和值中包括

两个类似样品的监测结果而含有两倍的误差[2]。将差值用于计算随机标准偏差

若s=sr则表明实验室不存在系统误差。当s＞sr时需进行方差分析：计算根据显著性水平（0.05）和自由度查表，若F≤F0.05()时，表明在95%置信水平时，实验室的系统误差对分析结果的可比性无显著性影响；若F＞F0.05()时，表明实验室的系统误差对分析结果的可比性具有显著性影响，应及时采取校正措施[2]。

3．数据融合技术的应用

数据融合技术是指利用计算机对按时序获得的若干观测信息，在一定准则下加以自动分析、综合，以完成所需的决策和评估任务而进行的信息处理技术。

人类通过人体器官感受外部信息，转换成生物电，并通过人的中枢神经传送到大脑进行综合分析处理，然后对外面环境进行判断和控制。而多传感器数据融合的基本原理就如同人脑综合处理所感受的信息：利用多个传感器感测外部环境信息，再把多个传感器的数据根据某种准则进行组合，以获得对被测对象的一致性解释和描述，从而得出更为准确的可信的结论。

面对大量的环境监测任务，如何科学有效地获取数据信息是最为关键的一步，融合技术为我们提供了强有力的支持，然而这些数据在采集、利用过程中，由于传感器采集数据的特征性差异，造成数据存在模糊性、互补性或矛盾性。如何有效并准确地处理传感器所采集的数据是以后研究的重点，而这必将为环境监测数据研究带来重大性突破。

3.1 融合模型

20世纪80年代，代表性的数据融合模型有[3-6]：英国情报环模型、美国JDL模型和Boyd控制环模型。20世纪90年代提出的“改进的JDL模型”[3]在军事领域应用十分广泛，还有将融合过程划分成观测、定位、决策、行动及传感器管理等阶段，并组成一个大循环的“综合模型”（Omnibus Model）[6]等。但由于以上模型均未引入自学习和多级反馈机制，使得其自适应性和自我完善功能有待提高。

目前融合算法主要有： Kalman滤波器的改进方法[7,8]和“数值－语言”混杂条件下的“知识发现和数据挖掘”（KDDM）[7]方法和面向分布式数据融合的支持向量机（SVM）[9]方法等。

3.2 应用举例

由于Kalman 滤波方法是解决最优化滤波问题的经典方法，故常用于从被噪声污染的观测信号中消除噪声影响，可将Kalman 滤波方法用于环境采样数据真实值的估计，在此我们以大气监测为例，简单探讨Kalman 滤波方法在环境监测方面的应用[10]。

（1）建立大气变化状态转移矩阵。根据环境科学相关领域知识，结合传感器采集的大气参数，建立关于这些参数的大气参数状态转移矩阵。利用该矩阵，研究各项大气参数的变化情况。

（2）根据（1）中得到的观测目标属性特征，对来自各传感器的，反映不同污染现象的观测数据进行分析，分解出反映各种不同的污染现象的参数向量值。

（3）根据大气变化状态转移矩阵，利用各传感器采集的大气参数观察值，对各大气采样站点的环境进行最优化估计，得到各项参数的最优化估计值。

4．结论

（1）对环境监测数据的可疑值判断和取舍方法进行了研究，同时还探讨了监测结果的统计方法和实验室监测质量的统计方法。

（2）简单展望了未来数据融合技术在环境监测方面的应用，并以大气监测为例进行分析。

[1] 叶萍. 浅议环境监测数据的审核[J]. 中国环境管理干部学院学报，2010，（2）：45-46.

[2] 马彦峰，张勇. 环境监测数据结果评价[J]. 环境保护科学，2010，（1）：23-25．

[3] Linas J， Bowman C， Rogova G， et al. Revisiting the JDL data fusion model Ⅱ[C]// Proceedings of the Seventh InternationalConference on Information Fusion. Stockholm， Sweden，2004， 2：1218-1230.

[4] Kalandros M K， Trailovic L， Pao L Y， et al. Tutorial on multisensor management and fusion algorithms for target tracking[C]//Proceedings of the 2004 American Control Conference. Boston，Massachusetts， 2004，5：4734-4748.

[5] 何友，王国宏，陆大金等. 多传感器信息融合及应用[M].北京： 电子工业出版社，2000.

[6] 潘泉，于昕，程咏梅等. 信息融合理论的基本方法与进展[J]. 自动化学报，2003，29（4）： 599-615.

[7] Gao J B， Harris C J. Some remarks on Kalman filters for the multisensor fusion[J]. Information Fusion，2002，3（3）：191-201.

[8] Sun Shuli， Deng Zili. Multi-sensor optimal information fusion Kalman filter[J]. Automatica，2004，40（6）： 1017-1023.

[9] Challa S， Palaniswami M， Shilton A. Distributed data fusion using support vector machines[C]//Proceedings of the 5th Intl. Conf. on Information Fusion，2002，2：881-885.

[10] 邵 斌，蒋云良，张建宏. 面向环境监测数据的融合方法研究[J]. 心智与计算，2008，2（1）：42-47 .

Processing and analysis on environmental monitoring data

Yan Hui
（Taixing Environmental Monitoring Station,Taixing，225400）

Environmental monitoring is an important means of protecting environment.With the development of science and technology, processing and analysis of monitor in data has been great improved,which prodive a strong protection for human beings. Collecting data was studied in this article,as well as analysis and research on environmental monitoring data on multiple perspectives,and investigated new methods used in the field of monitoring data.

environmental monitoring，monitoring data，data fusion

X708

A

1674-6252（2012）03-0051-04