远程数据采集系统的可靠性仿真研究
2012-09-20敖长林陈红光
于 嵩,敖长林,陈红光
(1.东北农业大学工程学院,哈尔滨 150010;2.东北农业大学理学院,哈尔滨 150030;3.东北农业大学水利与建筑学院,哈尔滨 150030)
近年来,随着单片机系统的不断发展,单片机在精准农业、工业自动化、生产过程控制、智能化测试仪器仪表等领域的应用越来越深入。由于测控系统所处的环境越来越复杂,各种不同形式的干扰都在影响系统的正常运行;有来自系统内部和外部的各种电气干扰,还有系统的结构设计、元器件的选择、安装和制造工艺等因素的影响,均可降低单片机系统的可靠性,主要表现在系统数据采集误差大、控制状态失灵、数据发生变化等方面[1]。
远程数据采集系统可以实现数据的实时准确采集和远距离传输,在精准农业中占有重要地位,其可靠性高低直接影响测产系统的信息传输质量,进而影响机器系统的作业效果,研究其可靠性对农业生产具有重要意义。
本文采用计算机仿真技术对系统进行可靠性分析,利用故障树分析和蒙特卡罗相结合方法,对远程数据采集系统进行可靠性仿真,找到影响系统可靠性的各种不利因素,从而采取相应预防措施。
1 系统工作原理和失效分析
1.1 远程数据采集系统的的工作原理
本系统设计的硬件电路由两个模块组成,分别是采集模块和通信模块;采集模块在现场进行数据采集和处理,通过有线或者无线设备与通信模块进行数据通信,通信模块还要与计算机进行串口通信。系统硬件电路如图1所示。采集模块由模数转换电路、单片机电路、串并转换电路、调制解调电路组成。该模块完成模拟量向数字量的转换,数据处理,信号的调制,信号的功率放大及发送等功能。通信模块由调制解调电路,串并转换电路,单片机电路组成,主要完成信号的接收和放大,并与计算机进行串口通信。

图1 系统硬件电路原理Fig.1 System hardware circuit
1.2 系统的失效分析及其故障树
故障树分析法(FAT),是一种评价复杂系统可靠性与安全性的重要方法。FAT把系统事件作为故障树的顶事件,用规定的逻辑符号表示,找出导致事件所有可能发生的直接因素和原因,它们是处于过渡状态的中间事件,并由此逐步深入分析,直到找出事故的基本原因,即故障树的底事件为止,这样逐层的建立系统故障树。该系统由两套单片机系统和连接二者的有线或无线设备组成,单片机应用系统的硬件电路构成比较复杂、所用元件品种繁多,工作场所环境复杂,所以系统失效的因素也比较多。
由于外界干扰和电源内部噪声等影响,可使电源发生故障,电源故障则会导致系统供电不足或运行故障。在实际的工业现场,存在着大量的复杂的干扰信号,可导致采集模块的组成电路发生故障,如传感器故障、模数转换电路故障、调制解调电路故障等。导致通信模块故障的原因是由于外界干扰(如空间电场磁场干扰)的存在,出现信道故障,单片机电路故障,接收电路故障,通信电路故障等。根据以上分析建立本系统的故障树,如图2所示。

图2 系统的故障树Fig.2 System fault tree
2 系统的数字仿真原理及过程
2.1 仿真模型的建立
2.1.1 系统组成
由图2可知,远程数据采集系统的故障树含有9个底事件,用S表示系统,则有:
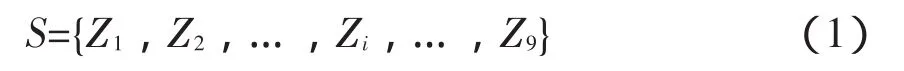
其中Zi(i=1,2,…,9)表示底事件,已知每一个底事件的失效分布函数均为指数分布,设为:

其中λi(i=1,2,…,9)为失效率。
2.1.2 可靠性仿真逻辑关系
如果故障树的一些底事件都发生时将会引起顶事件发生,那么这些底事件组成的集合就称为这个故障树的割集;若将割集中所含的底事件任意去掉一个就不再成为割集,则该割集称为最小割集。对系统建立的故障树,用下行法[2-3]求出其所有最小割集为9个。
以Mi(i=1,2,…,9)表示最小割集,根据最小割集的定义,只要有一个最小割集发生,则顶事件必然发生,而该最小割集中的底事件必全部发生,所以,顶事件Φ和最小割集及其包含的底事件之间的逻辑关系表示为:

2.2 系统可靠性仿真原理及过程
系统可靠性仿真利用Monte Carlo方法[4]产生0~1之间的均匀随机数,代入到基本部件的失效分布函数的反函中,得到底事件的失效时间。仿真时,在每个最小割集范围内找出失效时间最大的部件,该部件失效时,该割集中所有的部件已经失效,从而说明系统失效。由于最小割集之间的关系为或的逻辑关系,所以对所有失效时间最大值再排序,找出其中最小值,就是系统的失效时间[5-6]。仿真过程如下:
2.2.1 初始数据
本系统的基本部件的失效分布函数均为指数分布,总仿真次数为10 000次,系统最大工作时间为25 000 h,最小割集数目为9个,即所有的底事件。
2.2.2 底事件的失效时间
已知基本部件的失效分布函数及参数,利用反函数法求得第i个底事件Zi失效时间为:

其中f(u)是基本部件的失效分布函数,f-1(u为其反函数,u为0~1之间分布的随机数。
2.2.3 系统的失效时间
不失一般性,若系统有k个最小割集,每个割集中有p个基本部件。
①取p个抽样时间,取k次,每次取的抽样时间必须满足随机性和独立性的要求,代入到最小割集中,得:

这样可得到每个最小割集的抽样时间T1,T2,…,Tk。
②对k个最小割集抽样时间令TT=min{T1,T2,…,Tk},得到时间等价于系统做一次仿真试验的失效时间。
③重复1)、2)步n次,得到系统失效时间的实现值序列:TT1,TT2,…,TTn。
④在仿真运行期间,记录所需的统计量,在仿真结束之后,整理并输出各种统计量。
本文研究的系统k取9,p取1,n取10 000,则最终得到系统失效时间:TT1,TT2,…,TT10000。
2.2.4 仿真结果统计分析
仿真完成后,需要对仿真的数据进行统计。利用文献[5]中的区间统计法进行系统失效数的分布统计,进而算出系统可靠性指标,得到系统总失效率为:1.253×10-4·h-1,系统平均无故障工作时间(MTBF)为:7 980 h。图3给出了系统仿真的流程。
3 仿真实验结果分析
本系统的故障树由4个门事件和9个基本部件组成。应用Matlab7.0开发了相应的软件,软件程序框图见图3。系统最大仿真时间设为25 000 h,仿真运行10 000次,把各基本部件失效率、故障树割集等数据输入仿真软件并运行,可以得到系统可靠度曲线、基本部件模式重要度直方图,如图4、5所示。
由图4可以看出,系统可靠度曲线近似符合失效规律为指数分布的曲线形式。由曲线可以得到,系统可靠度达到50%时,对应的时间为7.1×103h,约为10个月,系统的可靠度达到90%时,对应的时间为1 240 h,这种情况说明要保持系统高可靠性运行,就要开始使用约为51 d内对系统做一次检查比较合理。

图3 系统仿真程序框Fig.3 System simulation block

图4 系统可靠度曲线Fig.4 System reliability curve
由图5可知,基本部件3、4的模式重要度大,说明这些部件失效最容易引起系统失效,应该重点维护,及时维修。
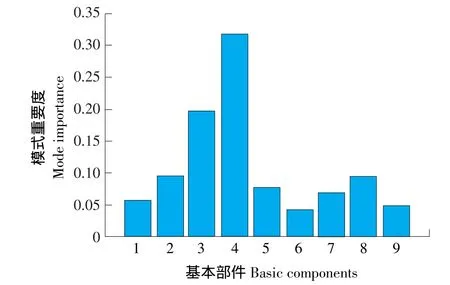
图5 基本部件模式重要度直方图Fig.5 Mode importance of the basic components of the histogram
4 结论
本文采用故障树最小割集和蒙特卡罗相结合的方法对远程数据采集系统进行数字仿真,得到系统可靠性相关指标的曲线,即可靠度和失效率曲线;可靠性仿真可显著降低远程数据采集系统可靠性试验费用和缩短试验周期,研究结论将为远程数据采集系统使用管理、维修提供理论参考依据。
[1]洪志刚.单片机应用系统设计[M].北京:机械工业出版社,2011.
[2]魏选平,卞树檀.故障树分析法及其应用[J].计算机科学与技术,2004(3):43-45.
[3]金星,洪延姬,沈怀荣,等.系统可靠性数值分析方法[M].北京:国防工业出版社,2002.
[4]肖刚,李天柁.系统可靠性分析中的蒙特卡罗方法[M].北京:科学出版社,2003.
[5]袁立峰,王浚.可靠性数字仿真方法及其应用[J].电子产品可靠性与环境试验,2005(2):17-20
[6]杨为民,盛一兴.系统可靠性数字仿真[M].北京:航空航天大学出版社,1990.
