振动式深松中耕作业机的振源部件设计及有限元分析

2012-09-20李紫辉张忠学

东北农业大学学报 2012年2期

赵铃，董欣，李紫辉，张忠学

（东北农业大学工程学院，哈尔滨 150030）

深松耕法可以打破犁底层、加深耕作层及改善土壤的透气透水性能，具有蓄水保墒、提高地温和增加产量的作用。但深松机具的牵引阻力随耕深的增加而增大，是田间能耗最大的机具。研究表明，在各种减阻节能措施中，振动减阻的效果尤为明显[1-3]。为了打破犁底层，提高降水资源的有效利用率，针对这一技术研发出配套机具—振动式深松中耕作业机，论文阐述了其关键部件—振源部件的设计过程，为机具的研究和合理使用提供了理论基础。

1 机具结构关系及工作原理

1.1 结构关系

机具主要由机架1、振源部件2、缓冲部件3、悬挂4、限深部件5、深松部件6和中耕部件7等组成，如图1所示。深松部件对称布置于机架中横梁两侧，中耕部件分别配置于机架的中横梁和相应深松部件后部的后横梁上，限深部件装于机架前横梁的两侧，振源部件通过螺栓固装在机架上。

1.2 工作原理

机具振源部件、缓冲部件、深松部件和中耕部件相配合，实现苗期雨季到来之前垄向隔垄深松和中耕的联合作业。作业时，拖拉机动力输出轴通过万向联轴器将动力传至由一对带偏心块的齿轮机构组成的振源部件，齿轮啮合带动偏心块旋转产生离心力使深松部件产生上下振动，土层疏松；与此同时，位于深松部件后面连接于机架的中耕部件完成中耕起垄整地的连续作业，限深部件限制松土深度，机具工作时松土深达30 cm，由于振动降低了牵引阻力。

图1 振动式深松中耕联合作业机结构Fig.1 Subsoiling vibration and intertillage machine

2 振源部件设计

2.1 激振形式及激振力

2.1.1 激振形式

能够使机具工作部件产生振动的方式有机械式、液力式和气力式。本机具选用机械式激振形式，直接通过拖拉机动力输出轴获得振动动力源[4]。振源部件主要由偏心块、齿轮，主动轴、从动轴及箱体构成，见图2。

图2 振源部件Fig.2 Vibration source

机具作业时，拖拉机的动力输出轴通过万向联轴器将动力传递给振源部件主动轴Ⅰ，通过一组传动比为1的齿轮啮合将运动传递给从动轴Ⅱ，带动固装在两轴上的偏心块旋转产生离心力，通过机架使深松部件产生上下振动，实现振动深松作业。

2.1.2 激振力

振源部件利用偏心块旋转运动产生的离心力获得激振力为F，见图3，其大小：

因质量相同的两偏心块的传动轴以相同转速反向旋转，故离心力的水平分量大小相等，方向相反，相互抵消；垂直分量大小相等，方向相同，相互迭加，即：

式中，r-偏心块质心距旋转轴中心距离（m）；m-偏心块质量（kg）；ω-偏心块角速度（rad·s-1）；θ-离心力与水平方向的夹角。

Fy即为带动整个机具产生上下振动的激振力，其方向与振源部件传动轴轴线垂直，大小随θ的变化而改变。

图3 离心力Fig.3 Schematic diagram of centrifugal force

2.2 振源部件的设计

2.2.1 传动齿轮齿数的确定

考虑振源部件中齿轮结构及偏心块结构的配置及工作要求，选择齿轮模数m＝10，两传动轴中心距L＝170 mm，根据：

联立式（3）、（4）得： z1＝z2＝17

2.2.2 偏心块设计

偏心块结构见图4，为避免振源部件中的偏心块与传动齿轮发生干涉，偏心块连接传动轴凸缘部分的厚度需大于偏心块厚度，其内径和外径尺寸由传动轴结构设计得到，d＝47 mm，D＝64 mm。

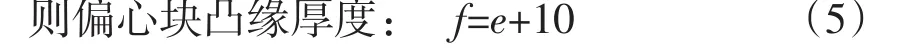
偏心块的半径R和厚度e大小的确定按其所产生最小激振力大于整机重量的3%设计，即：

以偏心块重量最小为目标函数：

式中，F-激振力（N）；m1-机具重量（不含偏心块）（kg）；m-偏心块的重量（kg）。

图4 偏心块结构Fig.4 Structure of eccentric block

其中，激振力F由式（2）通过计算两个偏心块离心力垂直分量最大值的合力获得，即F＝2mω 2Y；机具重量（不含偏心块）由其三维建模获得m1＝513.93 kg；偏心块的重量及质心距传动轴距离计算如下：

式中，ρ-偏心块密度（g·mm-3）；偏心块选用45 钢，密度ρ＝0.00787 g·mm-3，角速度ω＝18π（rad·s-1）；V-偏心块体积（mm3）；为简化运算，设偏心块由四部分组成（忽略键槽），总体积：

其中，对于偏心块V1-半径R、厚度e的半圆柱体体积（mm3），V1＝πR2e/2；V2-直径D、厚度e的半圆柱体（挖空）体积（mm3），V2＝[π（D/2）2e]/2；V3-直径D、厚度f的圆柱体体积（mm3），V3＝（D/2）2f/2；V4-直径 d、厚度 f的圆柱体(挖空)体积mm3，V4＝π（d/2）2f/2。

偏心块质心距旋转轴的距离即为其质心在y轴上坐标Y（因对称性，x轴上的坐标为0），即：

式中，Y1、Y2、Y3和Y4分别为偏心块四部分体积 V1、V2、V3和 V4相对应部分的质心坐标，Y1＝4R/3π；Y2＝2D/3π；Y3＝0；Y4＝0。

以式（7）即偏心块重量最小为目标函数，式（6）为约束条件，利用MATLAB编程求解偏心块半径R和厚度e，得到最优解R＝134.8080 mm，e＝63.6295 mm，m＝14.35 kg。

设计时选择偏心块厚度e＝60 mm，满足式（6）的R＝137.23 mm，取偏心块半径R＝137.5 mm。

3 振源部件从动轴部装受力及有限元分析

机具工作时，振源部件为整个机具提供激振力，为保证作业安全可靠，选择振源部件中包含齿轮和偏心块的从动轴部装采用有限元法基于ANSYS软件对其进行全区域内强度分析，为设计提供理论依据。

3.1 基于MATLAB的振源部件从动轴部装受力分析与求解

3.1.1 振源部件从动轴部装受力分析

振源部件从动轴部装受力分析，如图5所示。工作中，齿轮受驱动力f3，输出轴两端轴承受力分别为f1、f2、f4和f5，从动轴、齿轮和偏心块的重力分别为G1、G2和G3，偏心块离心力F与竖直方向（Z方向）夹角为θ，其质心至轴中心距离为r。

图5 从动轴部装受力分析Fig.5 Force diagram

对从动轴受力分析，其平衡方程：

在xoy平面内

其中，从动轴重力G1＝35.67 N，质心距轴左端距离a＝123 mm，两支撑点距离d＝258 mm；齿轮压力角20°，分度圆半径R＝85 mm，重力G2＝57.3 N，距轴左端距离b＝125.5 mm；偏心块重力G3＝140 N，距轴中心距离r＝57.47 mm，距轴左端距离c＝178 mm，离心力F＝14×（18π）2×0.05747＝2 572.8N。

3.1.2 基于MATLAB的从动轴部装受力求解及解析模型建立

联立式（11）～（14）及式（16）即可得到从动轴的受力解。但偏心块的质心位置随θ由0°～360°变化，工作中传动轴的受力随时间而变化，故使力求解计算过程复杂化。论文利用MATLAB进行编程求解[5-6]，从动轴一个旋转周期内受力的图形表达见图6。

图6 受力结果Fig.6 Drawing of force results

由图 6 可知，从动轴的受力 f1、f2、f3、f4和 f5均具有周期性，且与轴的旋转周期一致呈现类似三角函数曲线的形式，故将其受力结果用数学解析式三角函数fi＝Aisin（ωt）+Bi（i＝1、2、…、5）进行表达，利用MATLAB进行数据拟合得到从动轴受力关于运动时间的数学表达为：

上述解析函数检验误差见图7。

图7 函数误差Fig.7 Drawing of function error

由图7可知，拟合函数与图6的图形表达的数据误差小于3%，故式（17）～（21）为从动轴部装受力结果的真实解析表达。

3.2 基于ANSYS从动轴部装的有限元分析

3.2.1 有限元模型建立、网格划分及材料属性定义

将已建立的从动轴部装三维模型导入ANSYS软件的解析环境，装配到一起模拟真实装配体状态；网格划分采用自动划分节点单元，见图8。

其中，从动轴、齿轮、偏心块材料均为45钢，调质处理，弹性模量E＝206 GPa，泊松比Py＝0.28，屈服极限σs＝355 MPa，静载安全系数n＝1.2，许用应力[σ]＝296MP（GB/T1222-1984）。

3.2.2 施加约束和载荷

从动轴受轴承支承的两端施加轴承载荷，其大小为式（17）、（18）、（20）和（21）；齿轮受力作用点为齿轮的啮合点处，大小为式（19）；各零件重力以合力形式施加；从动轴施加旋转作用，定义旋转角速度ω，其两端施加固定约束。

图8 网格划分Fig.8 Meshing the model

3.2.3 后期处理及结果分析

对从动轴部装在整个周期中求解，其解中最大应力时的变形云图、应力云图及应变云图分别见图9～11。

图9 变形云Fig.9 Deformation chart

图10 应力云Fig.10 Stress chart

图11 应变云Fig.11 Strain chart

由图9可知，工作时从动轴部装最大变形发生在偏心块外边缘处，其值为2.32×10-3mm；由图10可知，最大应力发生在从动轴与齿轮配装处，其值为6.19 MPa小于许用应力[σ]＝296 MPa，满足强度要求；图11为应变分布云图，应变分布规律与其应力分布云图一致，最大应变发生在从动轴靠近齿轮配装附近，其值3.09×10-5，与理论相吻合。

试验机具在实际作业过程中，偏心块在旋转的过程中所产生的离心力能激励整个机具的振动，实现振动深松的目的；并在满足打破犁底层所需要的耕深前提下，机具工作性能可靠，结构强度满足要求。