基于Lau效应测量光波长的讨论

朱岱巍，林伟华，张 硕，姚 金

（武汉大学物理科学与技术学院物理教学实验中心，湖北武汉430072）

基于Lau效应测量光波长的讨论

朱岱巍，林伟华，张 硕，姚 金

（武汉大学物理科学与技术学院物理教学实验中心，湖北武汉430072）

利用双光栅Lau效应测量光波长的原理，提出了筛选有效数据的方法，并详细讨论了通过测量两光栅间距和Lau条纹周期分别计算波长的可行性问题.通过综合考虑对实验可能产生影响的各种因素，认为利用两光栅间距计算波长虽然标准差较大，但相对偏差小，结果更接近真实值，是一种可行的方法；但利用Lau条纹周期计算的波长看似标准差小，但与真实值的相对偏差较大，从统计和实验的观点来说该方法是不可行的，只能作为一种参考方法.

Lau效应；光波长；测量精度

1 引 言

扩展光源照明相隔一定距离串联的2个光栅可在无穷远处形成高对比度的条纹，这一现象是在1948年由Lau首次利用间距z0＝kd2／（2λ）（式中：d为光栅常量，λ为光波长，k为整数）的2个全同光栅观察到的［1］，被称为双光栅Lau效应.20世纪80年代，有多课题组利用多种理论对Lau效应现象及产生的条件展开解释和扩展，如Lohmann等人利用衍射理论分析了在z0＝kd2／（2λ）条纹分布［2］，Gori和Sudol等人分别利用相干理论进行解释［3－4］，并将条件扩展为z0＝αd2／（βλ）（式中α和β互为质数），Patorski利用Talbot效应进行解释［5］，并进一步将Lau效应条件拓展为2个不同周期光栅，Swanson等人利用光栅成像解释并将条件扩展为任意两光栅［6］；在国内也有利用杨氏干涉模型解释Lau效应［7］，还有提出了二维光栅的Lau效应［8］.Lau效应可产生高对比度的条纹，也为该效应带来广泛的应用，如测量折射率、焦距、波长［8－10］、光学编码［11］、表面成像［12］等.此外，双光栅结构还有其他的应用，如基于双光栅衍射效应的测量微振动［13］，等等.根据Lau效应理论，两光栅间距和Lau条纹周期均与光波长有关，因此可通过测量这2个量来计算光波长，在文献［8］中曾使用Lau条纹周期来计算波长，但至于利用哪个测量量求光波长可获得更高精度，并未有文献详细讨论.

本文用2个全同的一维光栅实现Lau效应，综合影响实验测量的各种可能因素，系统地比较和分析了利用两光栅间距和Lau条纹周期分别计算波长的可行性和精度问题.

2 实验原理

如图1所示，单色扩展光源S照明2个相距z0的全同光栅，在透镜L的后焦平面P上形成条纹，基于交叉谱密度函数推导［4］可知当光栅间距满足透镜焦平面上的光强分布为

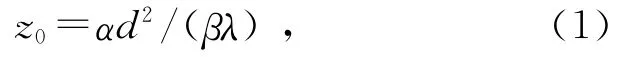
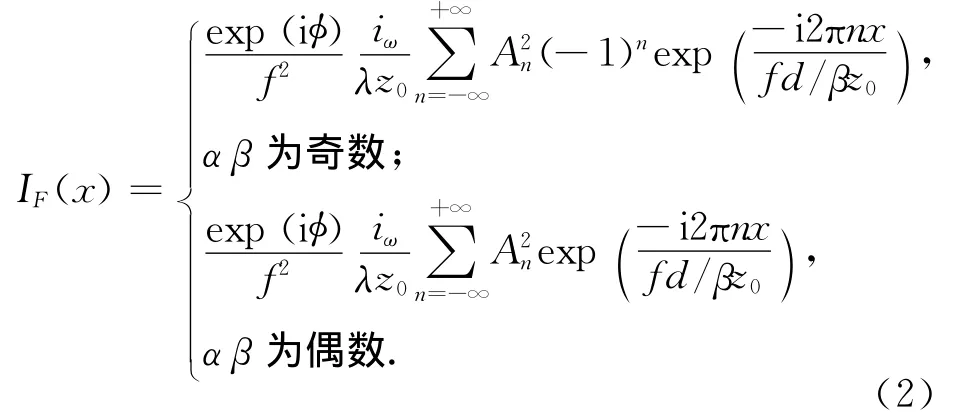
图1 实验装置示意图

式中

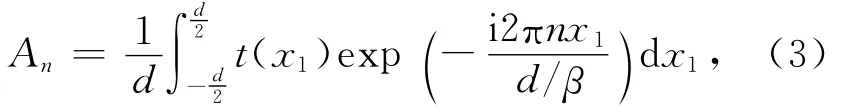
其中t（x1）为光栅的透过率函数.

由（2）式可知，焦平面上的条纹周期为

亮纹的宽度为［4］

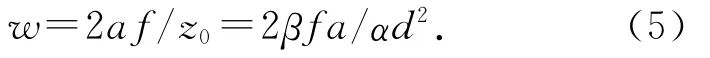
式中：a是一维朗奇光栅在1个周期内透光部分的长度.

亮纹宽度与条纹周期比值：

由（6）式可知β值越小，亮纹越细锐.

由（1）和（4）两式可知，在观测到清晰的Lau效应条纹时，通过测量两光栅的间距z0或条纹的周期D来计算光波长是可行的，但必须在实验过程中确定α和β值.由（4）式可以看出α小，则屏上的条纹周期D大，这样将会减小条纹的测量误差；另外，如果β越小，则光栅间距z0也会较大，则z0值的测量误差也会减小.因此，可以认为α＝β＝1是测量的理想条件.可采用如下的步骤来测量和筛选出有效的计算数据（即α＝β＝1的z0和D）：

1）任意调节两光栅的间距，当观察到清晰的条纹后测量条纹周期D和光栅距离z0，利用（4）式计算β值，并筛选出符合β≈1的D和z0数据；

2）在由1）判别后获得的数据中，根据D与α成反比的关系，确定这些因α值不同而产生的各种D中的最大值，并且视为这些数据是满足条件α＝β＝1的可用于计算的有效数据，并利用（1）或（4）式计算λ.

3 实验结果

实验中G1和G2是2块全同光栅，光栅常量为d＝500μm，占空比为a∶d＝1∶10，透镜L为JJY型分光计望远镜的物镜，其焦距为f＝170.6mm（由焦距仪测量）.

在扩展光源波长未知的情况下，通过改变两光栅的间距，得到最清晰的条纹，然后利用测微目镜测出30个条纹的间距求出条纹周期D，并通过上述数据筛选方法获得用于计算λ的有效数据.通过数据筛选，并确定了满足条件α＝β＝1的两光栅间距z0的范围后，采用2种测量方法来精确的测量λ：第一种称为不固定z0法，即每次通过在小范围内移动其中1个光栅获得清晰的Lau条纹，测量光栅间距z0，并利用（1）式计算λ；第二种称为固定z0法，即首先需要确定1个理想的光栅间距（如可利用第一种方法获得光栅间距的平均值），并将两光栅的间距固定为此值，然后再测量条纹间距D，并利用（4）式计算λ.2种方法多次测量的数据分别如表1和表2所示，数据处理和分析如下（实验用钠光灯的标准波长值为589.3nm）：

1）根据表1中测量的z0用（1）式计算波长λ＝（588.1±1.8）nm，相对偏差为0.203%［14］.将样本均值加减1倍标准差的范围内包括了标准波长值.

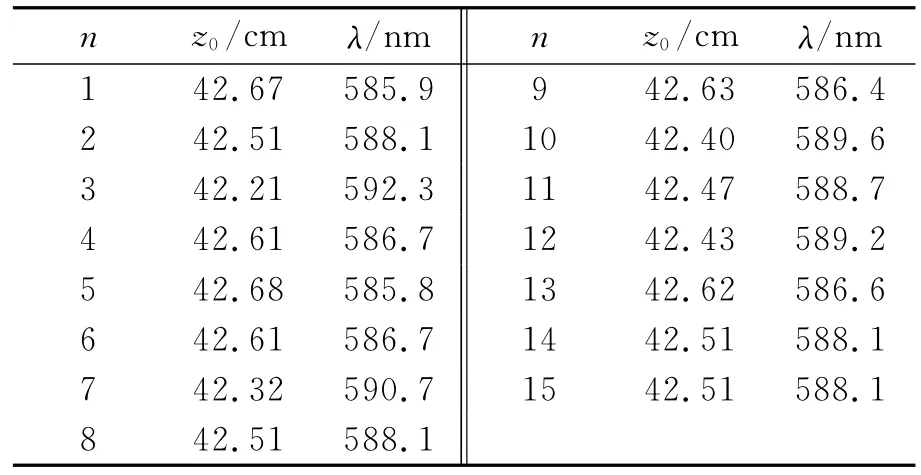
表1 不固定z0测量法测量结果

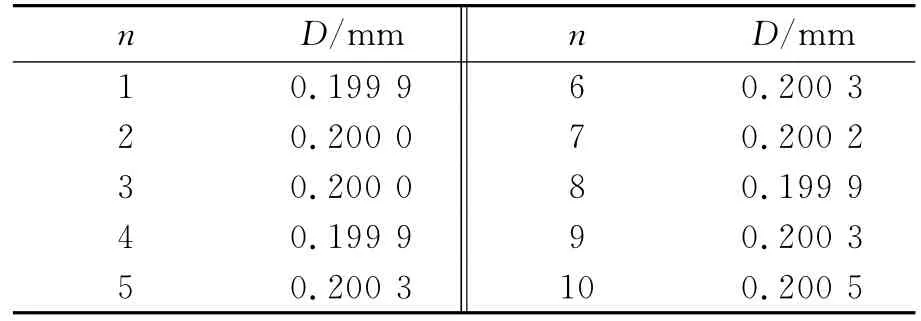
表2 固定z0测量法（z0＝42.51cm）测量结果

4 测量精度分析

因光栅在什么位置能出现最清晰的条纹完全凭实验者主观判断，因此对成像的判断成为不固定法的主要误差来源.在实验中，感觉最敏锐的操作者也无法在0.5cm的范围内分辨清晰度的差异，即使采用二分法判断，偏差仍然不会小于0.2cm.满足α＝β＝1的z0标准值是42.42cm，从理论上，测量的相对偏差应为0.47%.另一方面是钢制直尺的系统误差，钢尺测量精度通常为10－3m，由于z0的精确值就在m的量级，所以误差范围为0.1%的数量级.因此，从这两方面来说，表1中测量数据已达到较高的精度.

固定z0法的误差来源有两点：1）测微目镜的系统误差和测量误差；2）两光栅间距的取值是主要的误差来源.因为采用此方法测量，首先需要确定理想的光栅间距.在实验中采用多次判断获得均值，虽然已非常接近光栅间距的标准值，但仍有误差.根据钠黄光的标准波长计算的标准条纹间距为0.201 1mm，而实际在z0＝42.51cm情况下多次测量的条纹间距均值为0.200 1mm，且标准差较小.所以该法获得的波长值的相对误差较大，但标准差较小以致于无法通过假设检验的水平.为了进一步证实这种分析，将z0设置到偏小的值，条纹间距测量结果如表3所示，¯D＝0.201 5mm，计算得¯λ＝590.5nm，标准差s＝0.9nm.结果如理论分析偏大，与上面的分析相一致，而且标准差仍然很小，这再次验证了上面的分析.但必须强调，在未知波长的情况下采用多次判断测量取平均来确定z0是最客观、最好的办法，所以固定z0法不能作为实际的测量方法，只能作为参考.

表3 光栅间距固定为z0＝42.20cm测量结果

5 结束语

数据的方法，并讨论了利用光栅间距和条纹周期分别计算波长的可行性.因利用Lau效应测量波长的测量精度在很大程度上受制于对成像清晰度的判断，在清晰度的判断一定的情况下，采用测量光栅间距求得的波长值相对误差小，但标准差较大，可通过假设检验，是一种可行的正确方法；而采用固定光栅间距，测量条纹间距求得的波长值，虽然方差小，但相对误差大，不能通过假设检验，是一种不可行的测量方法，只能作为参考方法.

［1］ Lau E.Beugungserscheinungen and dopperlrastern［J］.Ann.Phys.，1948，6：417－423.

［2］ Jahns J，Lohmann A W.The Lau effect（a diffraction experiment with incoherent illumination）［J］.Opt.Commun.，1979，28（3）：263－267.

［3］ Gori F.Lau effect and coherence theory［J］.Opt.Commun.，1979，31（1）：4－8.

［4］ Sudol R，Thompson B J.Lau effect：theory and experiment［J］.App.Opt.，1981，20（6）：1107－1116.

［5］ Patorski K.Incoherent superposition of multiple self－imaging Lau effect and moiréfringe explanation［J］.Opt.Acta，1983，30（6）：745－758.

［6］ Swanson G J，Leith E N.Analysis of the Lau effect and generalized grating imaging［J］.J.Opt.Soc.Am.A，1985，2（6）：789－793.

［7］ 张海联，海滨.用杨氏干涉模型解释Lau效应［J］.光学仪器，1992，14（6）：16－19.

［8］ 余飞鸿，梁荫中.利用Lau效应测定干涉滤光片的中心透过率波长值［J］.光学仪器，1991，5（13）：1－5.

［9］ Bhattacharya J C.Refractive index measurement［J］.Opt.＆Laser Tech.，1987，19（1）：29－32.

［10］ 王秋芬.利用双光栅Lau效应测量透镜焦距［J］.物理实验，2004，24（6）：13－15.

［11］ Crespo D，Alonso J，Morlanes T，et al.Optical encoder based on the Lau effect［J］.Opt.Eng.，2000，39（3）：817－824.

［12］ Thakur M，Quan C，Tay C J.Surface profiling using fringe projection technique based on Lau effect［J］.Opt.＆Laser Tech.，2007，39（3）：453－459.

［13］ 陈长鹏，汪礼胜.测量动光栅瞬时速度的有效方法［J］.物理实验，2010，30（7）：1－4.

［14］ 齐民友.概率论与数理统计［M］.北京：高等教育出版社，2002：180－210，

提出了基于Lau效应测量光波长筛选有效

Measurement of optical wavelength based on Lau effect

ZHU Dai－wei，LIN Wei－hua，ZHANG Shuo，YAO Jin
（Center of Fundamental Physics Teaching and Experiment，School of Physics and Technology，Wuhan University，Wuhan 430072，China）

The theory of measuring optical wavelength was introduced based on Lau effect，the method to obtain effective data was proposed，and the feasibility of calculating the optical wavelength by measuring the grating space and the period of Lau fringes，respectively，was discussed in detail.A general accounting of the possible reasons that could affect the experimental measurement indicated that the wavelength calculated with the grating space had a small relative error and a big standard deviation，this method was still feasible.However，the wavelength calculated with the period of Lau fringes had a small standard deviation but a big relative error，thus it was not a feasible method in the statistical and experimental view.

Lau effect；optical wavelength；measuring precision

O436.1

A

1005－4642（2012）10－0035－04

［责任编辑：郭 伟］

“第7届全国高等学校物理实验教学研讨会”论文

2012－03－22；修改日期：2012－05－28

国家基础科学人才培养基金（No.J1210061）；武汉大学本科生业余科研（No.S2011125）

朱岱巍（1991－），男，湖南长沙人，武汉大学物理学国家基地班2009级本科生.

林伟华（1977－），男，浙江开化人，武汉大学物理科学与技术学院讲师，博士，从事微纳光子学研究.