基于主成分分析的舰船装备维修费组合预测

谢 力 杨怀宁 尹相平 孙玉华

1海军工程大学装备经济管理系，湖北武汉430033 2海军装备部装备采购中心，北京100071 3海军装备部装备招标中心，北京100071 4中国人民解放军92493部队，辽宁葫芦岛125001

0 引 言

舰船装备维修费是保障舰船装备持续良好运行、发挥战斗力的关键所在。实现舰船装备维修费科学准确的预测，对提高海军装备经费的使用效益，进而提高海军装备的战斗力具有重要意义。但由于舰船装备的维修活动受内部和外部各种复杂因素的影响，如舰船造价、使用强度、维修技术、物价变化、维修制度等，再加上我国相关数据的收集工作起步较晚［1-2］，单一预测模型难以准确反映其变化规律。在实际应用中，费用分析人员一般根据不同来源的资料构建多种预测模型，对舰船装备维修费进行组合预测［3-4］，以提高预测的适应性和稳定性。

Granger和 Wei等［5-6］在回归框架中对多种组合方法进行了讨论，证明带有常数项且不受约束（限制权重为非负且权重和为1）的回归组合模型更具优势。但由于舰船装备维修费预测是典型的小样本问题，因此多种预测方法都可对其进行预测。运用基于回归的组合预测模型对其进行研究时，容易出现预测模型比用于组合预测的样本数量多，导致回归系数无法估计的情况。同时，Timmerman［7］发现在单项预测数量过多时，增加模型的代价（增加参数估计误差）与相应的收益（精度的提高）不匹配，故主张从组合中剔除那些只增加少量信息的预测模型以解决该问题。但是根据Granger和 Aiolfi等［8-9］的研究显示，对单一预测模型的修剪一般不存在一个普适的最优数量，且Aiolfi等［10］还发现，先前最好的模型在后来会变得最差，先前最差的模型在后来会变得较好。因此，通过剔除部分模型的方法并不能很好地解决该问题。并且，单项预测方法之间通常容易出现信息重叠的现象，即基于回归组合预测模型中的多重共线性问题，也将影响组合预测模型的性能。

主成分分析（Principal Component Analysis，PCA）［11］通过Karhunen-Loève变换，产生一组称为主成分的新变量，所有主成分互相独立，其间不存在冗余，并通过保留前面含信息量最大的几个主成分来实现降维。本文尝试在建立基于回归的舰船装备维修费组合预测模型之前，先采用主成分分析对单项预测模型进行降维处理，以解决预测模型多于用于组合预测的样本数量以及单项预测模型之间的线性相关问题，并结合实际问题进行应用分析。

1 主成分分析的基本原理

主成分分析由英国生物统计学家Pearson［12］于1901年在对非随机变量进行讨论时引入，随后数学家Hotelling［13］将其推广至随机变量。该方法将原来指标的信息重新组合成了一组相互独立的少数几个综合指标，这些综合指标可以尽可能保留原有指标所含有的信息，且各指标所含信息互不重叠。

设有m个指标组成的m维随机向量Y=(y1，y2，…，ym)′，作指标的线性组合：

为便于讨论，主成分分析将问题限制在单位圆中进行，即方程组（1）中的系数uij满足。根据信息理论的观点，一个系统所包含的信息量体现为其不确定性的大小。在统计分析中，一组数据的方差可以反映其不确定性，故数据中所含的信息量可通过其方差大小来度量。在方程组（1）中，Z1是 y1，y2，…，ym线性组合中方差最大的，因而含有最大的信息量，称为第一主成分。为保证各指标所含信息互不重叠，Z1，Z2，…，Zm互不相关，依次类推得到各主成分。

根据不同的数据特征和分析的需要，目前在传统PCA的基础上还产生了非线性PCA［14］、概率PCA［15］和核 PCA［16］等多种主成分分析方法。

2 基于主成分分析的组合预测模型

设 yt1，yt2，…，ytm是t时刻分别来自m个不同舰船装备维修费预测模型的拟合结果，舰船装备维修费实际值为 yt(t=1，2，…，n)，则基于回归的舰船装备维修费组合预测模型可以表示为：

式中，ytc表示组合预测；w0为常数项；wi（i=1，2，…，m）为相应单项预测方法的权系数；εt为随机扰动。

在我国装备发展采用“多研制、少生产”策略的背景下，同型号舰船都是小批量甚至单件生产，舰船装备维修费预测可参考的装备较少。再加上我国舰船装备修理实际发生费用数据长期统计不规范、装备修理部门或工厂的信息封闭等原因，导致舰船装备维修费预测时可利用的样本量小。因此，在采用式（2）构建舰船装备维修费组合预测模型时，经常会出现预测模型的数量比用于组合预测的样本数量多的情况，直接导致回归系数无法确定。针对这一问题，下面将采用主成分分析对单项预测模型进行降维处理，以满足方程（2）求解的需要。

设各预测方法拟合值组成的矩阵为：

由于舰船装备维修费各预测方法的拟合值并不存在量纲或数量级的差异，因此不需要对原始数据进行标准化处理，可以直接进行主成分分析，具体计算步骤如下。

步骤1：计算拟合值Y的相关系数矩阵 R=(rij)mm，其中rij是第i种预测方法与第 j种预测方法的相关系数。

步骤2：计算相关矩阵 R的特征值 λ1≥λ2≥…≥λm＞0 ，及其相应的特征向量 u1，u2，…，um。其中 ui=(ui1，ui2，…，uim)(i=1，2，…，m)，从而得到m 个主成分 Z1，Z2，…，Zm。

步骤3：根据上面得到的m个主成分，对第一主成分Z1作线性回归：

将不同时刻 t=1，2，…，n的 y和 Z1的值代入方程（5），求回归系数 α0和 α1，进行显著性检验，并计算回归方程的AIC（Akaike's Information Criterion）值［17］，记为 AIC1。

步骤4：在方程（5）中增加主成分 Z2，并分别建立线性回归模型：

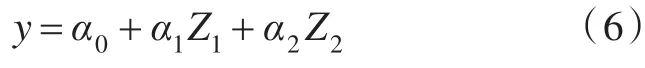
求解回归系数，进行显著性检验，并计算回归方程的AIC值，记为 AIC2。如果 AIC2＞AIC1，则表示方程（5）为最佳组合预测模型，可以用其对舰船装备维修费进行预测；如果 AIC2＜AIC1且回归方程统计上显著，则在回归方程中继续逐个增加主成分，直到后一个统计上显著的回归方程的AIC大于前一个统计上显著的回归方程的AIC，否则，将所有主成分加入其中。最后，使用得到的最佳组合预测模型对舰船装备维修费进行预测。

3 例证分析

以文献［18］中某单位舰船装备维修费的后7组数据为样本，另外增加几种预测模型的预测结果作为本文提出方法例证分析的基础。其中，以前面6组数据为校准样本，第7组数据为检验样本。舰船装备维修费及各单项预测模型预测数据样本如表1所示（单位为万元）。

表1 某单位舰船装备维修费及其预测Tab.1 Ship equipm entm aintenance cost and its budget

在表1中，因为用于组合预测的样本仅6个，而用于组合的预测模型有7个，显然直接采用基于回归的组合预测无法求解，所以下面将采用本文给出的方法进行例证分析。

1）取前6组数据，计算各预测方法之间的相关系数，结果如表2所示。

从表2中可看出，各单项预测方法数据之间的相关系数都在0.97以上，即各单项预测方法之间高度线性相关。这在预期之中，因为各种预测方法的拟合值都与舰船装备维修费实际值高度线性相关，因此它们之间自然也高度线性相关，即各单项预测方法存在多重相关性。

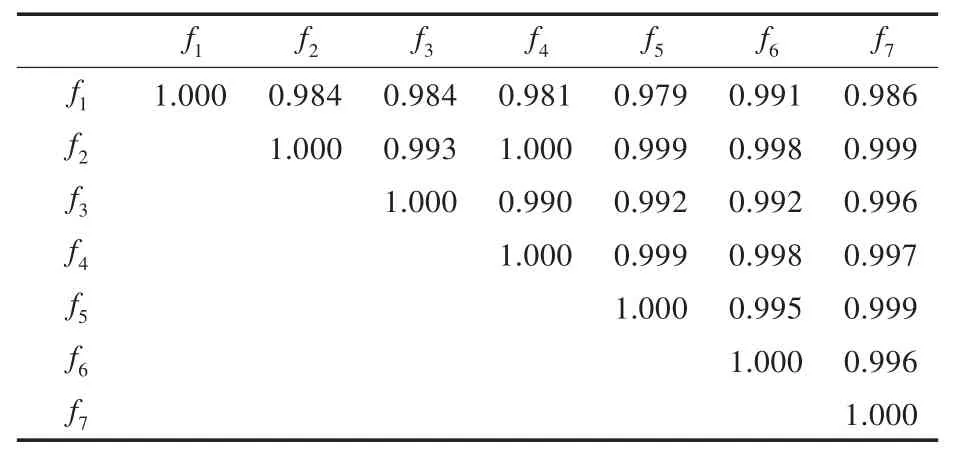
表2 各单项预测方法之间的相关系数Tab.2 Correlation coefficients between individual forecastm ethods

2）根据前6组数据，运用Matlab 7.1中的princomp（）函数计算各预测方法的主成分系数和新坐标下各主成分的值，分别如表3和表4所示。

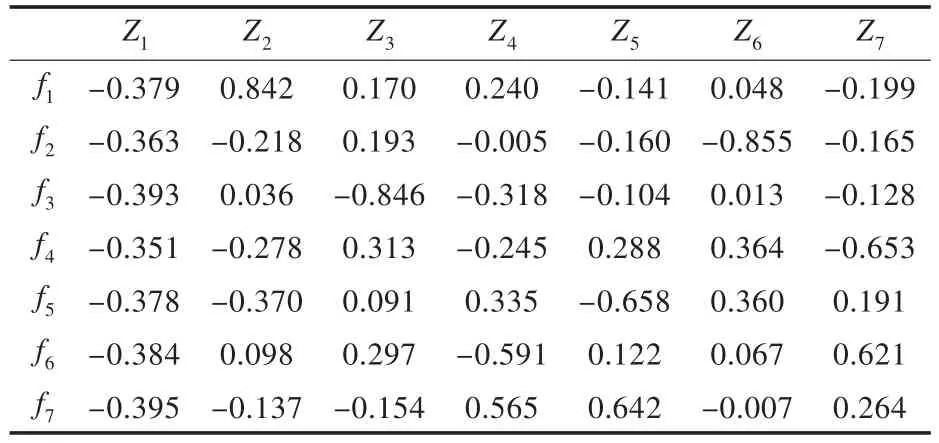
表3 主成分系数Tab.3 Principal com ponen t coefficien ts

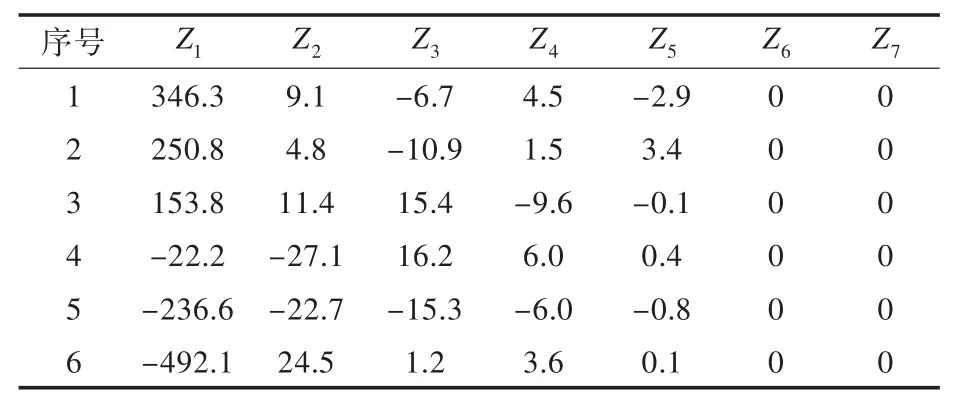
表4 新坐标下各主成分的值Tab.4 Principal com ponent values in new coord inate

从表4中可以看出，在新坐标下，最后2个主成分不包含任何信息，原数据维数得到降低。

3）运用Eviews6根据式（5）建立回归模型为：

将第2个主成分加入回归方程，再次计算回归模型，得到 AIC2≈7.891＞7.780，即带有一个主成分的回归模型即为最佳组合预测模型。

4）将第7组数据中各方法的预测值转化为主成分值，并将第一主成分值（计算过程见表5）代入上面的回归方程：

同时，还采用算术平均法、误差平方和倒数法、均方误差倒数法、简单加权平均法等常用组合预测［19-21］对本例进行了计算，结果如表6所示。

可见，通过本文提出的组合预测模型选择方法能有效改善组合预测的性能。

4 结 论

1）在建立基于回归的组合预测模型前，采用主成分分析对单项预测模型进行降维处理，可以有效解决预测模型多于用于组合预测的样本数量的问题。

2）主成分分析可以有效解决舰船装备维修费组合预测模型中的共线性问题。

表5 检验样本新坐标下第一主成分的值过程Tab.5 Calcu lating p rocess of the first p rincipal com ponent values of testing sam p le in new coordinate

表6 各组合模型预测值与预测误差比较Tab.6 Com parison of the forecast value and forecasterror am ong various com bination m odels

3）由于各种预测方法的拟合值都与实际值高度线性相关，因而舰船装备维修费各单项预测方法之间也高度线性相关。

4）采用AIC确定主成分的数量客观可行，可为在主成分分析中引入各种信息准则提供参考。

5）实例表明，基于主成分分析的舰船装备维修费组合预测模型具有良好的预测精度，且明显优于常用的组合预测模型。

此外，尽管本文给出的方法实现简单、应用方便，但由于PCA是以线性假设为前提，当各单项预测方法之间出现复杂的非线性关系时，本文的方法不能准确描述其关系，从而约束了本文方法的有效性。此时，必须结合非线性降维方法来建模组合预测模型。

［1］XIE L，WEIR X，JIANG T J，et al.Generalized PLS regression forecast modeling of warship equipment maintenance cost［C］//16th International Conference on Management Science and Engineering.Washington：IEEE Press，2009：607-612.

［2］谢力，魏汝祥，于伟宗.舰船装备维修费预测方法评价准则体系研究［J］.中国舰船研究，2011，6（2）：98-102.

XIE L，WEIR X，YU W Z.Evaluation criteria system of forecasting methods for maintenance cost of ship equipment［J］.Chinese Journal of Ship Research，2011，6（2）：98-102.

［3］谢力，魏汝祥，訾书宇，等.基于包容性检验的舰船装备维修费组合预测［J］.系统工程与电子技术，2010，32（12）：2599-2602.

XIE L，WEIR X，ZISY，etal.Combined forecasting of ship equipmentmaintenance cost based on encompassing tests［J］.Systems Engineering and Electronics，2010，32（12）：2599-2602.

［4］WEIR X，XIE L，YIN X P，etal.Combined forecasting of ship equipmentmaintenance costwith AHP and odds-matrixmethod［C］//The Proceedingsof2010 Conference on System Sciences，Management Sciences and System Dynamics.China， Beijing：Publishing House of Electronics Industry，2010（4）：115-122.

［5］GRANGER C W J，RAMANATHAN R.Improved methodsof combining forecasts［J］.Journalof Forecasting，1984，3（2）：197-204.

［6］WEIXQ.Regression-based forecastcombinationmethods［J］.Romanian Journal of Economic Forecasting，2009，10（4）：5-18.

［7］TIMMERMAN A.Forecast combinations［M］//ELLIOTTG，GRANGER CW J，TIMMERMAN A.Handbook of Economic Forecasting.North-Holland：Elsevier，2006：135-196.

［8］GRANGER CW J，JEON Y.Thick modeling［J］.Economic Modeling，2004，21（2）：323-343.

［9］AIOLFIM，FAVERO C A.Model uncertainty，thick modeling and the predictability of stock returns［J］.Journalof Forecasting，2005，24（4）：233-254.

［10］AIOLFIM，TIMMERMANN A.Persistence in forecasting performance and conditional combination strategies［J］.Journal of Econometrics，2006，135（1/2）：31-53.

［11］CAMACHO J，PIC J，FERRER A.Data understanding with PCA：structural and variance information plots［J］.Chemometrics and Intelligent Laboratory Systems，2010，100（1）：48-56.

［12］PEARSON K.On lines and planes of closest fit to systems of points in space［J］.Philosophical Magazine，1901，2（11）：559-572.

［13］ HOTELLING H.Analysis of a complex of statistical variables into principal components［J］.Journal of Educational Psychology，1933，24（6）：417-441.

［14］马丽艳，李宏伟.一种基于非线性PCA的卷积混合盲源分离算法［J］.电子学报，2008，36（5）：1009-1012.

MA L Y，LIH W.An algorithm based on nonlinear PCA for blind separation of convolutivemixtures［J］.Acta Electronica Sinica，2008，36（5）：1009-1012.

［15］宋怀波，路长厚，邱化冬.基于概率PCA模型的压印字符集本征维数确定方法［J］.光电子激光，2010，21（5）：754-757.

SONG H B，LU CH，QIU H D.Determine the intrinsic dimension of protuberant characters based on probabilistic PCAmodelingmethod［J］.Journalof Optoelectronics.Laser，2010，21（5）：754-757.

［16］王洪斌，肖金壮，王洪瑞.数控系统连接相关故障的核PCA监测方法［J］.制造技术与机床，2009，59（7）：94-97.

WANG H B，XIAO J Z，WANG H R.Monitoring method on connection dependent faults in numerical control system using kernel PCA［J］.Manufacturing Technology and Machine Tool，2009，59（7）：94-97.

［17］KOLASSA S.Combining exponential smoothing forecasts using Akaike weights［J］.International Journal of Forecasting，2011，27（2）：238-251.

［18］訾书宇，魏汝祥，周萍.基于RBF神经网络的舰船维修费预测［J］.中国水运（学术版），2007，2（5）：164-165.

ZISY，WEIR X，ZHOU P.Ship maintenance cost forecasting based on RBF neural network［J］.China Water Transport，2007，2（5）：164-165.

［19］ANDRAW IS R R，ATIYA A F，EI-SHISHINY H.Forecast combinations of computational intelligence and linearmodels for the NN5 time series forecasting competition［J］.International Journal of Forecasting，2011，27（3）：672-688.

［20］ANDRAWIS R R，ATIYA A F，EI-SHISHINY H.Combination of long term and short term forecasts，with application to tourism demand forecasting［J］.International Journal of Forecasting，2011，27（3）：870-886.

［21］DIKSC G H，VRUGT JA.Comparison of point forecastaccuracy ofmodelaveragingmethods in hydrologic applications［J］.Stochastic Environmental Research and Risk Assessment，2010，24（6）：809-820.