一类常系数线性微分方程特解的求法

李 岚

(闽西职业技术学院电气工程系，福建 龙岩 364021)

0 引言

n阶常系数非齐次线性微分方程的一般形式:

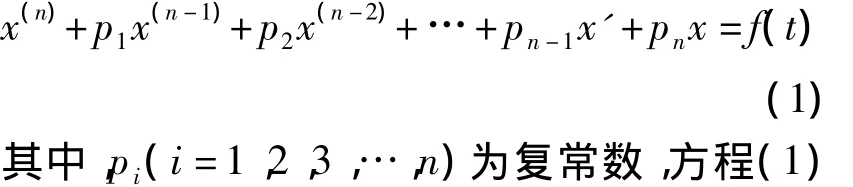
相应的齐次方程为:

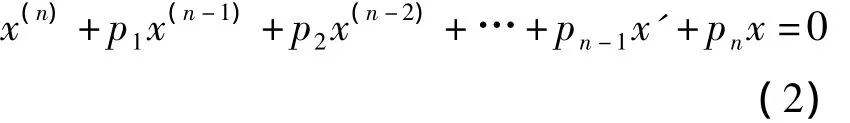
根据线性微分方程的通解结构理论，方程(1)的通解可以表示为方程(1)的一个特解与方程(2)的通解之和，而方程(2)的通解的求法一般采用Euler待定指数函数法(即特征根法)，因此要求方程(1)的通解，只要求出方程(1)的一个特解即可。

常系数非齐次线性微分方程特解的求法通常使用常数变易法、待定系数法、算子解法和拉普拉斯变换法，这些方法各具特色。如，待定系数法，虽然解题思路简单，易于掌握，但不具有一般性，计算比较繁琐，容易出错。本文先给出一阶常系数非齐次线性微分方程的特解求解公式，一阶常系数非齐次线性微分方程:

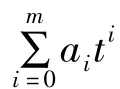
1 主要定理和性质

1.1 微分算子与逆算子及其性质

1.1.1 微分算子

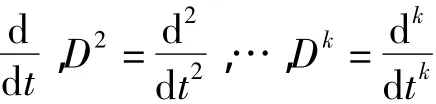
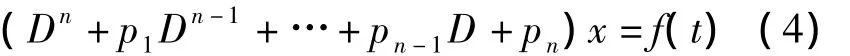
称P(D)=Dn+p1Dn－1+…+pn－1D+pn为算子多项式，方程(4)可简记为:

1.1.2 逆算子

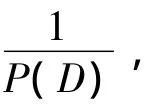
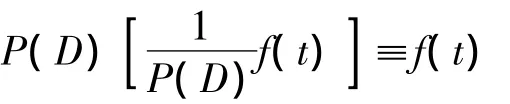
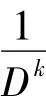
1.1.3 逆算子位移定理

1.2 基本定理

由不定积分公式:

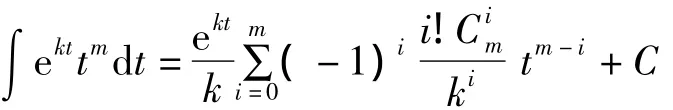
可推得:

定理1 设非齐次线性微分方程(3)对应的齐次方程的特征根为λ，则:

1)当α≠λ时，方程(3)一特解为:

2)当α=λ时，方程(3)一特解为:

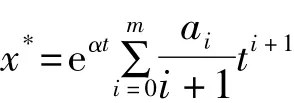
证明

1)当α≠λ时，由算子性质及引理1可得:

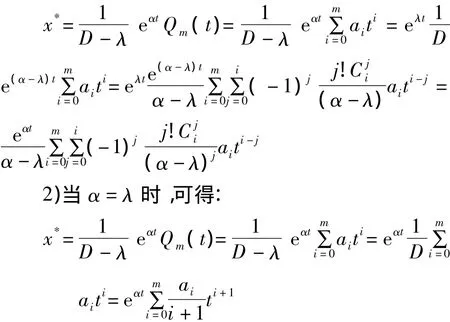
结论成立。

由于n次数多项式P(D)在复数范围内可因式分解为n个一次多项式的乘积，即P(D)=(D－λ1)(D－λ2)…(D－λn)(其中可能发生 λi=λj(1≤i，j≤n)的重根现象)，因此对于求n阶常系数非齐次线性微分方程(1)的特解时，可多次重复使用定理1，从而达到求解的目的。

2 应用举例

例1 求微分方程x'－2ix=e2t(4t+2)的特解。

解 对应齐次方程的特解是λ=2i。由自由项 e2t(4t+2)可知，α =2，a1=4，a0=2，且 α≠λ，所以所求非齐次线性微分方程的特解为:

例2 求微分方程x'－2x=(13t－4)cos 3t的特解。

解 对应齐次方程的特解是λ=2。微分方程中的自由项(13t－4)cos 3t可采用欧拉公式化为 Re[e3it(13t－4 ) ] 。可知 α=3i、a1=13、a0=－4，且α≠λ，所以所求非齐次线性微分方程的特解为:

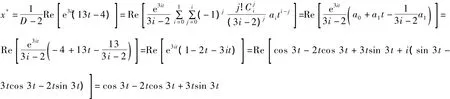
例3 求微分方程x″+5x'+6x=e－2t(t2+3t－5)的特解。

解 对应齐次方程的特解是λ1=－3，λ2=－2。由自由项 e－2t(t2+3t－5)可知，α =－2，a0=－5，a1=3，a2=1，且 α = λ2，所以所求非齐次线性微分方程的特解为:

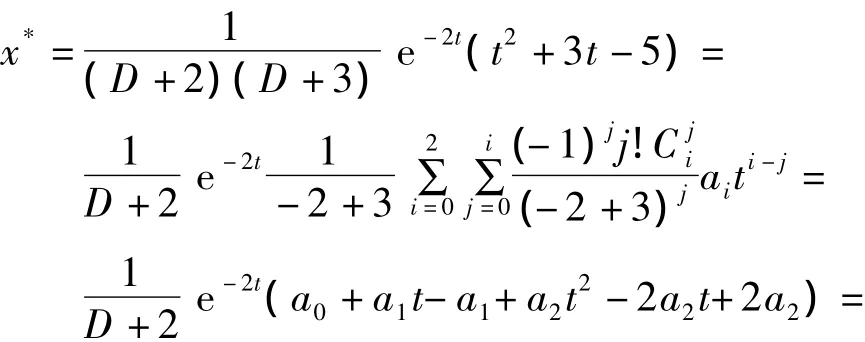
其中，b0= －6，b1=1，b2=1。

例4 求微分方程x‴－5x″+9x'－5x=et(3t2－13t+14)的特解。

解 对应齐次方程的特解是λ1=1，λ2=2+i，λ3=2 －i。由自由项 et(3t2－13t+14)可知，α =1，a0=14，a1=－13，a2=3，其中 αλ1所以所求非齐次线性微分方程的特解为:

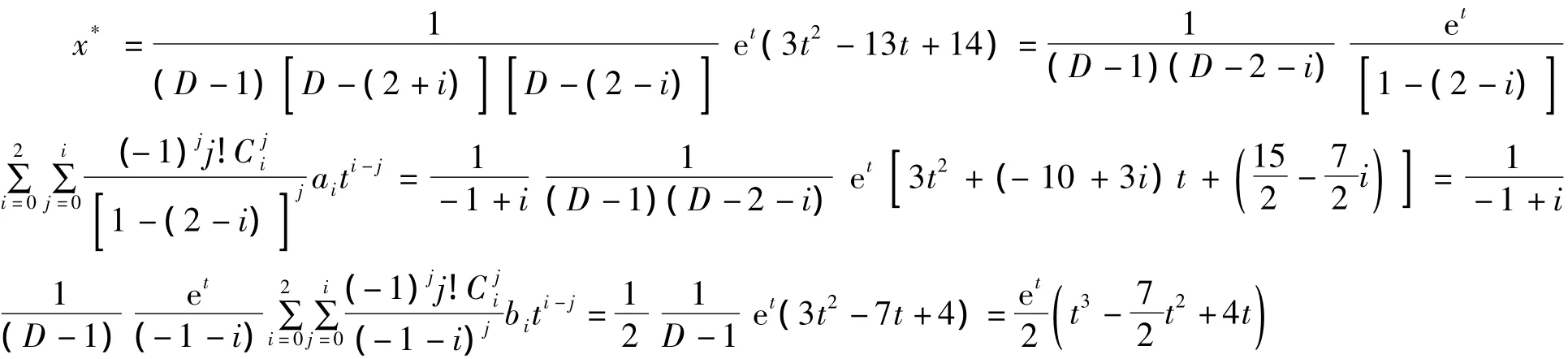
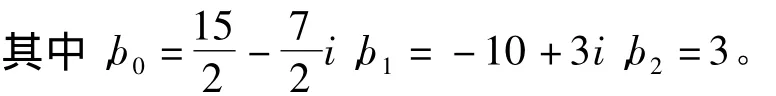
3 结语

本文针对一类一阶常系数线性微分方程(3)，运用积分公式和算子法推导了微分方程特解的求解方法，不仅方法较为简单，并可多次重复使用定理1计算出n阶常系数线性微分方程(1)当自由项f(t)=eαtQm(t)时)的特解，还能为求微分方程(1)的特解的解析解提供依据。

［1］王高雄，周之铭，朱思铭，等.常微分方程［M］.北京:高等教育出版社，2006.

［2］华东师范大学数学系.数学分析(下册)［M］.3版，北京:高等教育出版社，2002.

［3］同济大学教研室.高等数学(下册)［M］.4版，北京:高等教育出版社，1996.