基于最大似然可变子空间的快速说话人自适应方法

张文林 牛 铜 张连海 李弼程

(解放军信息工程大学信息工程学院 郑州 450002)

1 引言

在语音识别中，说话人相关(Speaker Dependent,SD)模型的识别性能比说话人无关(Speaker Independent,SI)模型要好得多[1]。然而实际中，由于难以获得充足的训练数据，直接训练SD模型往往是不现实的。对于一个实用的连续语音识别系统，需要利用少量的说话人相关数据对SI模型进行自适应得到SD模型，从而提高系统的识别性能。

说话人自适应方法通常可以分为三大类[2]：基于最大后验概率(Maximum A Posteriori,MAP)的方法、基于线性变换的方法和基于说话人聚类的方法。在基于MAP的方法中，假设SD模型参数服从某种先验分布，利用给定的自适应数据对模型参数进行最大后验估计，从而得到最大后验意义下的SD模型；这种方法具有良好的渐近性能，当训练数据越来越多时，可以得到较精确的SD模型。基于线性变换的方法，典型的代表是最大似然线性回归(Maximum Likelihood Linear Regression,MLLR)[3]，其基本原理是在最大似然准则下，估计一组线性变换对 SI模型参数进行变换得到 SD模型；相比MAP自适应方法，这种方法需要的自适应数据量较少，但渐近性能较差。而基于说话人聚类的方法则利用说话人之间相关性，通过训练集中SD模型参数的某种线性组合来逼近新的 SD模型参数。相比于前两类方法，这类方法需要估计的参数数量最少，适合于极少量自适应数据下的快速说话人自适应，其典型代表是基于本征音(Eigen Voice,EV)[4]的自适应方法和基于参考说话人加权(Reference Speaker Weighting,RSW)[5,6]的自适应方法。在本征音自适应方法中，通过对训练集中的SD 模型参数进行主分量分析(Principal Component Analysis,PCA)，找到SD模型参数的一组基；在自适应阶段，将新的SD模型参数限制在这组基所张成的子空间中，通过估计SD模型的坐标，从而达到快速说话人自适应的目的。而在RSW 方法中，用若干参考说话人模型参数的线性组合来逼近当前说话人相关模型。在文献[6]提出的可变参考说话人加权(Variable Reference Speaker Weighting,VRSW)算法中，在自适应阶段，根据“说话人系数”的大小动态选取与当前说话人最相似的若干个SD模型参数，进而重新计算其线性组合来逼近当前说话人相关模型。

近年来，尽管出现了各种基于2D-PCA[7]及基于张量分解[8]的说话人自适应方法，它们分别利用了SD模型参数的某种矩阵分解或张量分解的形式，需要估计的参数数量大于MLLR 方法，在自适应数据足分时，可以达到比MLLR方法更好的自适应效果，然而在少量自适应数据条件下，易于出现过训练的问题，性能反而不如经典的本征音方法。

本文针对基于隐马尔可夫模型的声学模型，研究其在极少量自适应数据下的快速说话人自适应方法。与经典本征音自适应方法的基本思想相同，新方法也是基于说话人子空间的，需要在训练阶段利用 PCA得到说话人空间的基矢量；与传统方法不同的是，新方法中说话人子空间不是在自适应前预先确定的，而是在自适应过程中动态选择的；在选择说话人子空间的方法上，与可变参考说话人加权算法[6]不同的是，子空间基矢量是直接通过最大似然准则选择的，而不是通过“加权系数”的大小进行选择，从而得到一种基于最大似然可变子空间的说话人自适应方法。根据子空间的维数是否固定，本文分别提出了固定维数最大似然子空间方法和可变维数最大似然子空间方法及其快速实现流程。在基于微软语料库[7]的连续语音识别实验中，在有监督和无监督的条件下，新方法均优于经典的基于本征音的方法和MLLR方法。

本文如下的章节安排如下：第2节简要给出了基于本征音的说话人自适应，并引入相关数学符号；第 3节给出了说话人子空间最大似然基的选取算法，及在此基础之上的固定维数与可变维数子空间说话人自适应方法；第4节给出了实验结果及分析；最后一节给出了本文的结论。

2 基于本征音的说话人自适应

设训练集中共S个说话人，声学特征矢量为D维，声学模型中共有M个高斯分量。令SI模型中第m个高斯分量的均值矢量和协方差矩阵分别为μm和∑m，对第s个说话人，其SD模型中第m个高斯分量的均值矢量为μm(s)。本文仅讨论声学模型中高斯分量均值矢量的自适应。

2.1 说话人子空间与本征音

在基于本征音的说话人自适应中，定义第s个说话人的超矢量为

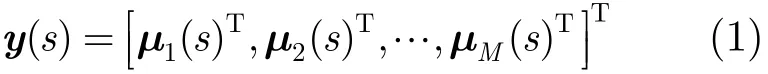
其中每一个说话人超矢量的维数为M×D维，则所有训练说话人超矢量Υ={y(s),s=1,2,…,S}构成了一个说话人子空间，其维数最大为S。对Υ进行主分量分析，最多可以得到S个基矢量，按其对应的特征值从大到小可以表示为e(1),e(2),…,e(S)，其中e(k)即称为第k个“本征音(eigenvoice)”。

在经典的本征音说话人自适应中，假设所有的说话人超矢量落入一个K维的子空间中(0＜K＜S)，则对于一个未知说话人相关模型，其说话人超矢量可以表示为

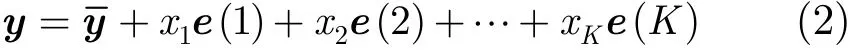
其中为训练说话人超矢量的均值矢量，xk为对应第k个本征音的系数。

估计未知说话人超矢量y在K维说话人子空间中的坐标即可进行说话人自适应，通常称x为“说话人因子(speaker factor)”。

2.2 基于说话人子空间的自适应方法

设自适应数据的特征矢量序列为O={o1,o2,…,oT}，其中T为语音帧数。采用最大似然准则和期望最大(Expectation Maximization,EM)算法，说话人自适应过程等价于求解如下最优化问题[3]：

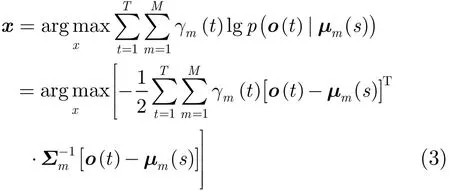
其中γm(t)表示第t帧特征矢量属于SI模型中第m个高斯分量的后验概率，给定自适应数据的标注，它可以通过经典的 Baum-Welch前后向算法[9]计算得到。

设第k个本征音e(k)中对应第m个高斯分量的子矢量为em(k)，高斯超矢量均值对应第m个高斯分量的部分为em(K)]，则。代入式(3)中的目标函数，并对x求导，令其导数等于 0，可以得到说话人超矢量的最大似然估计为

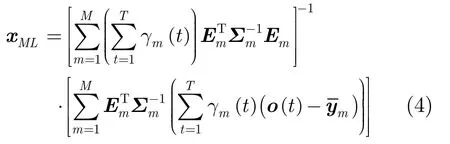
式(4)即为最大似然本征分解(Maximum Likelihood Eigen Decomposition,MLED)[3]求解说话人因子的表达式。

3 基于最大似然可变子空间的说话人自适应

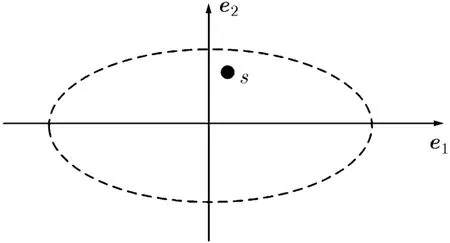
图1 2维说话人子空间示例

为了简单起见，图1中仅给出前2维本征音e(1)和e(2)所张成的2维子空间；虚线所示椭圆表示训练说话人在这2维子空间中的分布，由于第1个本征音e1所对应的特征值较大，训练说话人在其上分布的方差也越大，对应图1中表现为椭圆长轴。然而，对于某一个说话人s(实心圆圈所示)，其在第2个本征音e2上的坐标值大于第1个本征音e1上的坐标值，所以若强制选择1维的子空间，应该选择由e2所确定的1维子空间，而不是e1所确定的子空间。实际中说话人子空间维数K的典型值取为10～20，在这种较高维子空间中，说话人分布的稀疏性将会更为明显，上述现象也将会更为突出。因此，简单地取前K个最大特征值对应的本征音所张成的子空间作为所有测试说话人的子空间是不合理的。本节将讨论如何在最大似然准则下，针对每个说话人选取最优的子空间。

3.1 最优本征音选择

最优子空间的确定，其本质上是最优基矢量的选择，即最优本征音的选择。在RSW算法中，最佳参考说话人的选择也可以视为说话人子空间中一组非正交基的选择；在文献[6]提出的 VRSW 算法中，通过参考说话人模型的加权系数来进行选择，然而加权系数与EM算法的目标函数是不完全一致的，因此从最大似然的角度来看，选择得到的这组参考说话人模型并非“最大似然基”。因此，本文的算法思路是，针对每一个本征音，假设说话人超矢量落入其张成的1维子空间中，计算对应的最大似然说话人因子及其对数似然值(即 EM 算法的目标函数值)；选择似然度最大的K个本征音作为最优子空间的基矢量，这样所得到的基矢量可以认为是“最大似然基矢量”，所得到说话人子空间可认为是“最大似然子空间”。

在说话人子空间的基矢量仅由ek组成的情况下，由式(4)，最大似然说话人因子的计算可简化为

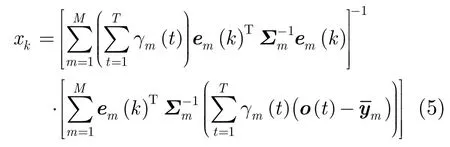
式(5)即为忽略各本征音之间相关性的说话人因子估计公式。由此得到对应说话人相关模型均值矢量为，将式(5)结果代入式(3)中的目标函数，整理可得其对数似然值为

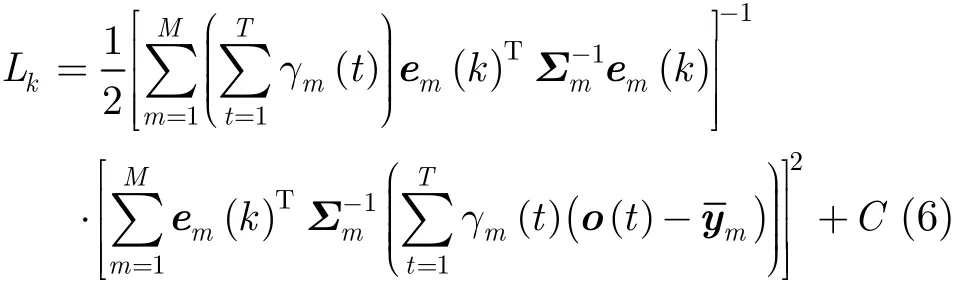
其中C为与本征音e(k)无关的常数项。

因此，对每个可能的本征音e(k)(k=1,2,…,S)，计算式(6)，并对其从大到小排序，对应的前K个本征音即为最大似然意义下的最佳K维说话人子空间的基，设其为{(k),k=1,2,…,K}，根据式(4)重新进行最大似然本征分解，即可得到该最佳K子空间下说话人因子。

3.2 基于固定维数最大似然子空间的快速说话人自适应算法实现流程

上述基于最大似然子空间的说话人自适应算法可以高效地实现，具体算法流程如下：

(1)预先选定说话人子空间维数K(1≤K≤S)；

(2)计算M×S2个加权内积，其中1 ≤m≤M,1 ≤k1≤S,1≤k2≤S；

(3)在给定自适应数据及其标注情况下，进行状态强制对齐及Baum-Welch前后向算法，累积其零阶和一阶充分统计量，即和

(4)利用(1)中预先计算好的加权内积值，计算

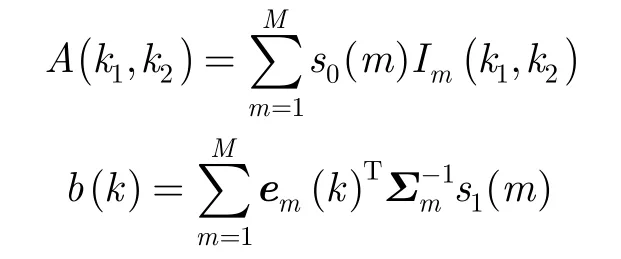
其中 1 ≤k1≤S,1 ≤k2≤S,1≤k≤S；

(5)计算Lk=b(k)2/A(k,k)(即式(6))，1≤k≤S；对其从大到小进行排序，选择前K个最大的kL，设其所对应的序号分别为l1,l2,…,lK；

(6)由(3)中计算结果，构造矩阵

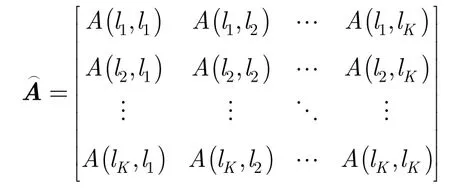
3.3 基于可变维数最大似然子空间的快速说话人自适应算法

在3.2节中，最大似然子空间维数K的选择是一个难点，需要通过多次试验来确定。本节给出一种基于可变维数最大似然子空间的快速说话人自适应算法。其基本思想是，通过最大似然本征音的对数似然值计算一个门限，对于其它本征音，只有当其似然值大于该门限时才被保留。此时，3.2节中算法流程的(1)，(4)，(5)步分别替换为：

(1)选定门限值α(0＜α＜1)；

4 实验结果及分析

为了验证本文算法的有效性，我们针对一个典型的连续语音识别系统进行了实验。实验语料采用微软语料库[10]，其中训练语料包含100个男性说话人，每个人200句话，共约33 h的语音数据；测试语料包含另外20个男性说话人，每人20句话，每句话大约5 s的话音。实验中，特征参数采用13维美尔频率倒谱系数(Mel-Frequency Cepstral Coefficients,MFCC)及其一阶差分和二阶差分，总的特征矢量维数为39维。基线系统中的SI模型利用开源隐马尔可夫模型工具包(Hidden Markov Toolkit,HTK)[9]训练得到，采用上下文相关的三音子有调音节作为声学建模单元，采用自左向右带自环无跳转三状态的HMM模型，每个状态8个高斯混元，利用HTK进行三音子聚类后共19136个高斯混元。训练阶段利用基于回归树(32个回归类)的MLLR自适应方法得到100个训练说话人相关模型，进而利用PCA得到100个本征音矢量。测试阶段解码器采用HTK自带的一遍解码器HVite，不采用语法模型，解码参数配置与文献[10]中相同。在说话人自适应实验中，分别从每个测试说话人语音中随机抽取1句话(小于5 s)语音作为自适应数据，剩下的19句话作为测试数据，利用HTK中的HResult工具在所有测试语音上统计有调音节的平均识别率作为实验结果。

为了比较算法的有效性，我们分别实现了基于MLLR的自适应和经典的基于本征音的自适应方法。对于本征音(EV)方法和固定维数最大似然可变子空间(MLEV)方法，分别在说话人子空间维数K取为10,20和30的情况下进行了实验。对于可变维数最大似然子空间(VMLEV)方法，对门限α取为0.1,0.08和0.06的情况分别进行了测试，并对测试说话人的平均最大似然子空间维数(用表示)进行了统计。各种自适应方法均在有监督(给定自适应数据标注)和无监督条件下(不给定自适应数据标注)分别进行了实验。自适应实验结果汇总如表1所示，其中基线系统(SI模型)的有调音节平均识别率为52.71%(文献[10]中报道结果为51.21%)。

由表1的实验结果可以看出，对于MLLR算法，由于自适应数据量过少(每个测试说话人平均少于5 s)，无法进行有效的自适应，有调音节平均识别率相比SI模型几乎没有任何提高。

对于经典的本征音自适应算法，系统平均识别率可以得到较大的提高，随着说话人子空间维数的增加，所需要估计的参数个数也相应地增加，识别率先增后降。

对于本文提出的固定维数最大似然子空间的方法，相比经典的本征音自适应算法，在相同的子空间维数下，识别率有了更进一步的提高。而对于可变维数最大似然子空间方法，可以在自适应阶段自动确定最大似然子空间的维数，具有更好的稳健性；当α=0 .08时，无论是在有监督还是无监督条件下，相比其它几种方法，均具有最佳的自适应效果。

实验中，我们还统计了在相同的子空间维数下，最大似然子空间方法与经典的本征音方法所选择的本征音基矢量的相同个数，平均统计结果如表2所示(括号外为有监督自适应实验统计结果，括号内为无监督自适应实验统计结果)：

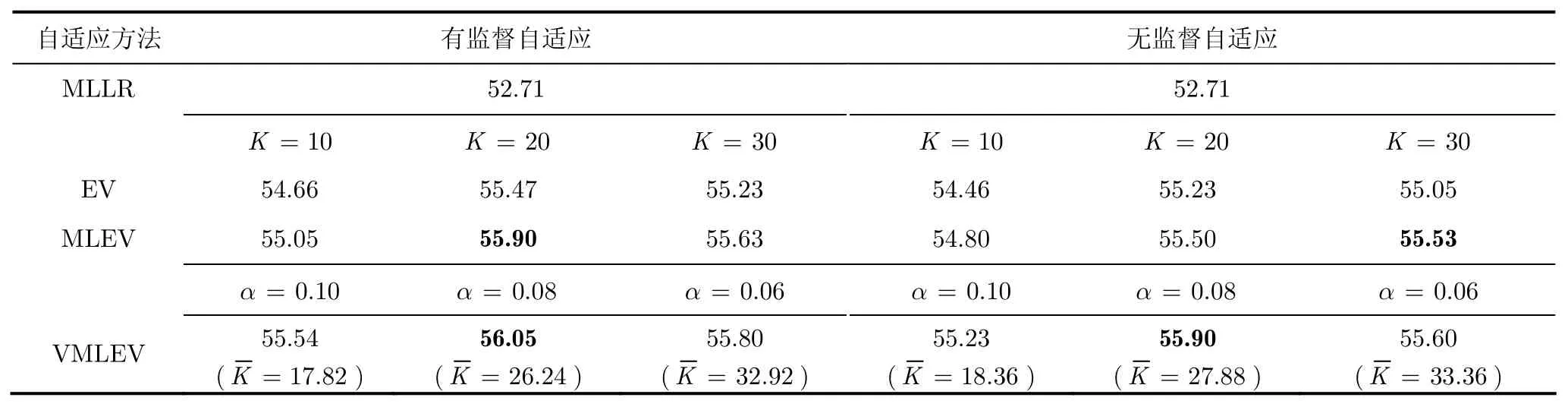
表1 一句话(5 s)自适应实验结果(有调音节平均识别率)

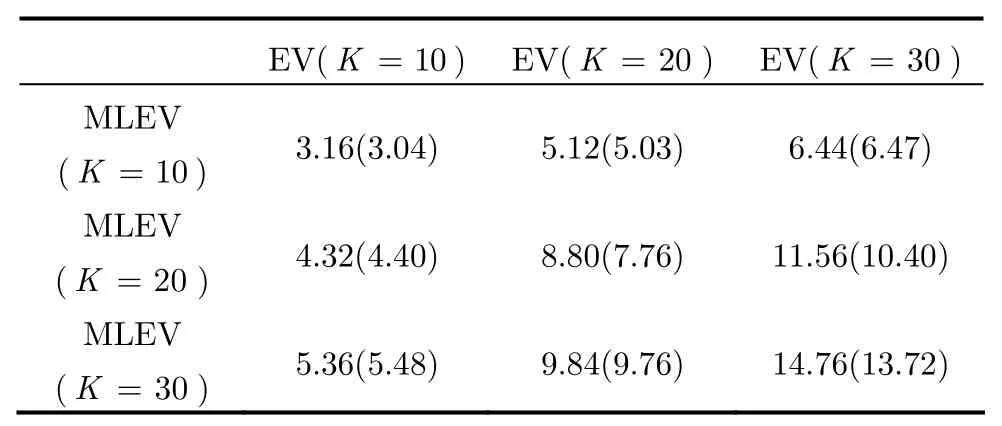
表2 VMLEV与传统本征音方法的相同本征音个数的平均值

由表2可以看出，在经典的本征音自适应方法中根据最大特征值所确定的K维子空间，对于每一个测试说话人而言并非是最佳的，需要提高子空间维数才能够尽量覆盖到最佳的子空间；但提高子空间维数就会增加所要估计的参数个数，在自适应数据量极少的情况下，这会增加过训练的风险。本文提出的最大似然可变子空间方法可以选择出最佳的K维子空间，通过自动确定子空间维数K，在尽量少的待估参数个数下得到尽可能好的自适应效果，有效地避免了过训练的问题。

5 结论

本文提出了一种基于最大似然可变子空间的说话人自适应算法。与经典基于说话人子空间的本征音自适应方法不同，新方法中说话人子空间的基矢量是在自适应阶段、通过最大似然准则动态选取的，从而可以得到尽量低维的(最大似然意义下的)最佳说话人子空间，进而可以在极少量的自适应数据条件下得到尽量好的自适应效果。实验结果表明，本文方法的自适应效果相比经典 MLLR方法和本征音方法均有明显的提高。

[1]Lee C H,Lin C H,and Juang B H.A study on speaker adaptation of the parameters of continuous density hidden Markov models[J].IEEE Transactions on Signal Processing,1991,39(4)：806-814.

[2]李虎生,刘加,刘润生.语音识别说话人自适应研究现状及其发展趋势[J].电子学报,2003,31(1)：103-108.Li Hu-sheng,Liu Jia,and Liu Run-sheng.Technology of speake adaptation in speech recognition and its development trend[J].Acta Electronica Sinica,2003,31(1)：103-108.

[3]Ghoshal A,Povey D,Agarwal M,et al..A novel estimation of feature-space MLLR for full-covariance models[C].International Conference on Acoustics,Speech and Signal Processing,Dallas,Texas,USA,2010：4310-4313.

[4]Kuhn R,Junqua J C,Nguyen P,et al..Rapid speaker adaptation in eigenvoice space[J].IEEE Transactions on Speech and Audio Processing,2000,8(6)：695-707.

[5]Teng W X,Gravier G,Bimbot F,et al..Rapid speaker adaptation by reference model interpolation[C].Interspeech,Antwerp,Belgium,2007：258-261.

[6]Teng W X,Gravier G,Bimbot F,et al..Speaker adaptation by variable reference model subspace and application to large vocabulary speech recognition[C].International Conference on Acoustics,Speech and Signal Processing,Taipei,China,2009：4381-4384.

[7]Jeong Y and Sim H S.New speaker adaptation method using 2-D PCA[J].IEEE Signal Processing Letters,2010,17(2)：193-196.

[8]Jeong Y.Speaker adaptation based on the multilinear decomposition of training speaker models[C].International Conference on Acoustics,Speech and Signal Processing,Dallas,Texas,USA,2010：4870-4873.

[9]Young S,Evermann G,Gales M,et al..The HTK Book.HTK Version 3.4,2009.

[10]Chang E,Shi Y,Zhou J,et al..Speech lab in a box：a Mandarin speech toolbox to jumpstart speech related research[C].EUROSPEECH-2001,Aalborg,Denmark,2001：2799-2802.