一种新的去噪模型的分裂Bregman算法

郝 岩 冯象初 许建楼②

①(西安电子科技大学理学院 西安 710071)

②(河南科技大学数学与统计学院 洛阳 471003)

1 引言

图像去噪是图像处理中最基本的问题之一，其目的就是从所得到的带噪图像中恢复出原图像，即求原图像的某种最优意义下的估计值。通常，一个较好的去噪方法应该是在去除噪声的同时又能较好地保持图像的原有信息。传统的图像去噪方法，如中值滤波、高斯滤波等，主要是将图像的高频成分滤除， 因此，这些方法不可避免地会将图像的一些细节特征去掉，从而使得所恢复出来的图像在纹理区域看起来比较模糊。

近年来，变分、偏微分方程方法在数字图像处理中得到了广泛应用[1-5]。其中图像去噪的各项异性扩散模型(Perona Malik,PM)[1]以及全变差模型(Rudin Osher Fatemi,ROF)[2]是比较典型的代表。目前，ROF模型因其具有良好的保边性能而备受青睐，但是该模型在图像恢复过程中常常会出现阶梯效应，因此，继ROF模型之后，许多方法被提出去处理这个问题。特别地，Lysaker等人[6]提出用高阶偏微分方程(Lysaker Lundervold Tai,LLT模型)来克服阶梯效应，但高阶偏微分方程演化图像的边缘比ROF模型快， 所以经常在图像的边缘引起模糊现象。为了在去除噪声的同时既保持图像的边缘，又避免阶梯现象，Lysaker等人[7]又提出一个两步去噪模型(Lysaker Osher Tai,LOT模型)。实验表明LOT模型能够弥补ROF模型及LLT模型的不足，然而，该模型的收敛速度比较慢。因此，对LOT模型给出有效的加速算法显得十分必要。最近，一些改进的 LOT模型及算法被相继提出[8,9]。其中，文献[9]提出在 LOT模型中用一个辅助变量θ代替法向量n，然后再利用分裂 Bregman方法[10-14]对其两步分别进行数值求解。这样在一定程度上降低了原有算法的计算复杂度，从而实现加速收敛。

本文在研究LOT模型的基础上，提出了一种新的变分去噪模型。新模型由于耦合了两个变量，因此，在求解时，先利用交替极小化方法化原模型为两个简单的子模型，然后再利用分裂Bregman方法对其进行交替求解。由于两子模型对LOT模型中的两步从构成方式及计算方式上分别进行了改进，因此，实验表明，新方法不仅具有较快的收敛速度，而且在去噪过程中其去噪能力及保边性能均好于LOT模型。

2 LOT模型

从数学的角度来讲，图像去噪问题是一个不适定的线性逆问题。其数学模型为

其中u0是观察到的带噪图像，u是原图像，η是加性噪声。对于该不适定问题，一般可通过正则化方法来求解。关于式(1)，文献[7]建议用一个两步去噪模型(LOT模型)进行求解。其基本思想是：首先构造出图像等照度线的法向场，然后再根据该向量场重构图像。因此， LOT模型的第1步就是解下面优化问题

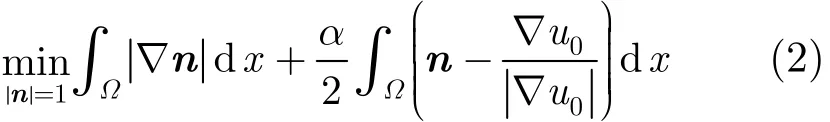
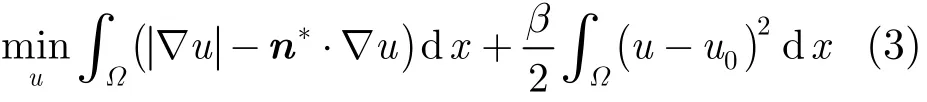
其中第1项为法向量逼近项，第2项为图像逼近项，β＞0 为惩罚参数。

LOT模型中由于使用低阶的偏微分方程，因此，它能够避免求解高阶偏微分方程时所引起的边缘模糊缺陷。实验表明，LOT模型在去噪的同时不仅能较好地保持图像的边缘，而且还能减缓阶梯效应。然而它的收敛速度比较慢。

针对上述缺陷，最近，文献[9]在对LOT模型改进的基础上提出了一种加速方法。通过用一个辅助变量θ，文献[9]将LOT模型等价地转换成下面模型

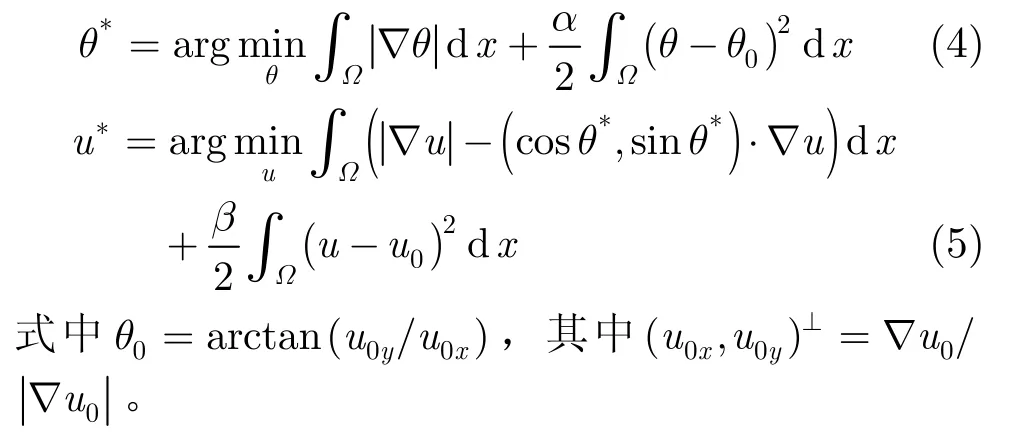
式(4)，式(5)与LOT模型中式(2)，式(3)相比，不但可以减少一个未知量的计算，而且还可以利用一些快速算法进行求解。文献[9]通过利用分裂Bregman方法实现了加速收敛。然而，在去噪效果上，文献[9]中方法并没有太大改进。

3 本文模型及其算法

3.1 模型建立

考虑到交替迭代方法的诸多优点，本文对式(1)提出一个同时包含变量θ和u的耦合去噪模型

式中前2项是正则项，后3项是保真项，λ,β1,β2和μ是正则参数。

由于式(6)中耦合了两个变量，因此首先采用交替迭代策略将其转化为下面两个简单的子模型：

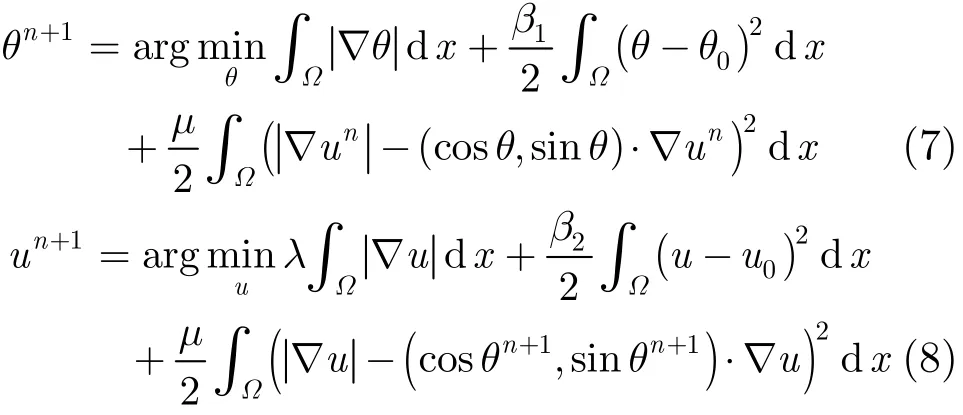
显然，通过式(7)可以构建角θ，而通过式(8)能够重构与θ角相适应的图像u。与式(4)，式(5)相比，式(7)，式(8)主要有以下两个不同点：

第一，模型的构成方式不同。式(7)在构建角θ时，保真项中不但要求θ逼近θ0，而且还要求(c osθ,sinθ)逼近法向量因此，式(7)比式(4)多出一个L2法向量逼近项，并且该逼近项还充分用到了上层重构出的图像nu。随着迭代的交替进行，包含nu的这个逼近项不断地对θ角进行校正，从而使其得到优化。然而式(4)在构建θ角时，保真项中仅仅要求θ逼近θ0，并没有利用到图像u。此外，在第2步重构图像时，式(8)比式(5)不仅多了一个全变差(Total Variation,TV)正则项而且还将原来的法向量逼近项换成了现在的L2法向量逼近项，并且此逼近项还能随θn+1不断地进行更新，最终使得重构图的法向量场逼近较优的向量场(cos˜θ,sin ˜θ)，这一点式(5)是无法比拟的。

第二，模型的计算方式不同。式(4)，式(5)在计算方式上是先计算式(4)，然后再根据式(4)结果计算式(5)，当达到停止标准时便结束迭代，并输出图像u*，在计算上这两步之间并不相互制约。然而,本文的式(7)，式(8)在计算上却相互制约，相互影响，交替计算。随着交替迭代的进行，重构出的图像u能够促使角θ进一步得到优化，反过来，优化后的θ角也使式(8)中的重构图像u向更优的方向演化，直到获得一个较好的图像为止。

3.2 算法提出

分裂Bregman方法是由文献[10]提出的一种高效的迭代方法，常用于求解带有L1项的优化问题。由于该方法具有编程简单，数值求解过程比较稳定，在计算过程中保持正则化参数为一个常数，占有内存小且具有较快的计算速度和收敛速度等优势，因此，这种方法已经被广泛地运用到图像处理中。本小节将采用该方法对式(7)，式(8)进行数值求解。

首先，在第 1个子模型式(7)中引入辅助变量ρx,ρy来处理不可微项然后再引入变量bx,by来更新迭代过程。最终，求解式(7)的迭代公式如下：

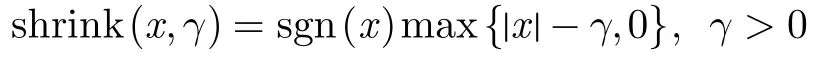
同样，在第 2个子模型式(8)中引入辅助变量ηx,ηy,cx,cy，用类似于上面的方法，可以推得式(8)的迭代公式为

其中

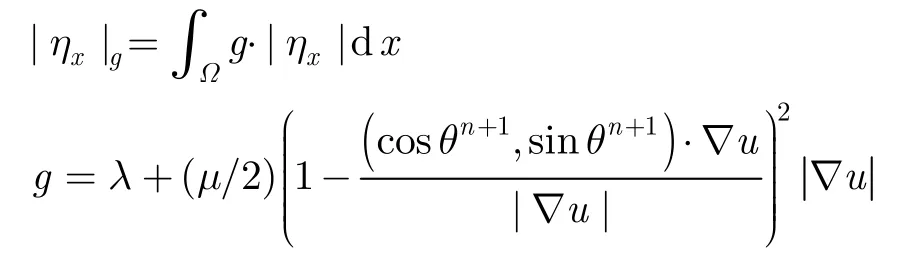
λ2为惩罚参数。结合式(9)和式(10)，给出本文算法。

新模型的分裂Bregman算法：

步骤 4 停止迭代：对ε＞0，当＜ε时，则停止迭代，并输出复原图像否则，令，转步骤2。

注：对于式(9)，式(10)中的第1个式子，本文都是运用Gauss-Seidel迭代求得。其具体的迭代公式分别为

此外，类似于文献[13]中的结果，新算法是收敛的。

4 数值实验

为了验证新算法的有效性，本节分别对两幅大小为256×256的带噪图像进行实验，并将新算法分别和文献[7,9]中方法进行比较。本文将从视觉效果与定量指标两个方面对图像质量进行比较。采用的定量指标有峰值信噪比(Peak Signal to Noise Ratio,PSNR)，均方误差(Mean Squared Error,MSE)和结构相似性(Structural SIMilarity,SSIM)。其定义分别如下：

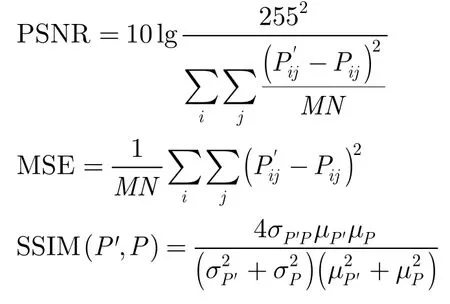
其中P为原始无噪图像，P'为恢复后的图像，M和N为图像尺寸大小，i,j为图像像素下标，σP',σP,μP',μP分别为P',P的标准差和均值，σP'P为P'和P之间的协方差。SSIM可以用来测量两图像之间的结构相似性，SSIM值越大，说明两图像的结构越相似。

图1 Lena 图实验结果

实验 1 选取细节丰富的结构图“Lena”作为测试图像。实验开始先对“Lena”图加入均值为0、方差为10的高斯白噪声。试验发现，新算法对参数β1不是很敏感，对参数λ,β2和μ较为敏感。大量的数值仿真结果表明，参数β1在0～1之间取值时效果较优。本实验中取参数λ=0 .5,β1=0 .1,β2=0.1,μ=0 .001。此外，为便于比较，取停止标准中参数ε=0 .01。图1给出了各种方法的去噪结果，其中图1(a)为含噪图，图1(b)为文献[7]方法(时间步长Δt=0.1)去噪后的结果，图1(c)为文献[9]方法(α=0 .15,β=0 .23)去噪后的结果，图1(d)为本文方法的处理结果，图1(e)，图1(f)，图1(g)分别为图1(b)，图1(c)，图1(d)的局部放大。比较3种去噪结果，可以看出，图1(b)和图1(c)中仍存在少量的块效应，如 Lena的额头、脸颊和下巴，而图1(d)看起来比较光滑、自然，并且对图像的边缘处理得也较好，如Lena的鼻梁比图1(b)和图1(c)都得到较好地保持，从放大的图像中可以很清楚地看到这一点。 图2给出了3种方法的峰值信噪比和均方误差随重构图时的迭代次数的变化曲线图。从图2(a)可以看出，本文方法在重构图像时仅需很少的迭代就可以达到稳定，并且其峰值信噪比的最大值高于其它两种方法，说明本文方法比其它两种方法具有较好的去噪效果。除此之外，本文方法还具有较快的收敛速度，这从图2(b)可以清楚地看到。

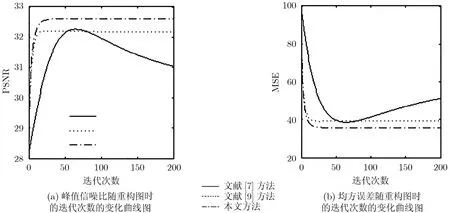
图2 实验1中峰值信噪比和均方误差随重构图时的迭代次数的变化曲线

实验 2 选取比较难处理的“Cameraman”图像作为测试目标，并对其加入均值为0、方差为15的高斯白噪声。“Cameraman”图像中不但含有像素跳跃区域(相机支架)、图像渐变区域(天空)，而且还含有图像震荡区域，或者说是纹理(如草坪)。试验中取参数λ=0 .8,β1=0 .05，参数β2,μ的取值和实验1的相同。图3给出了文献[7]、文献[9]方法和本文方法的去噪结果，其中图3(a)为噪声图，图3(b)为文献[7]方法(时间步长Δt=0.1)的去噪结果，图3(c)为文献[9]方法(α=0 .15,β=0 .14)的去噪结果，图3(d)为本文方法的处理结果，图3(e)，图3(f)，图3(g)分别为图3(b)，图3(c)，图3(d)与图3(a)的差图。从3种差图可以明显地看到，图3(e)中含有较多的边，而图3(f)与图3(e)相比，虽然含有较少的边，但也含有较少的噪声，这说明文献[9]中方法在保边方面要优于文献[7]中方法，但其去噪性能略弱于文献[7]。与前两种差图相比较，本文方法相应的差图中不仅含有较少的边，而且还含有较多的噪声，这说明了本文方法在去噪和边缘保持方面均优于其它两种方法。表1中的实验数据也从客观上表明了本文方法的优越性。

图3 Cameraman 图实验结果

表1列出了两实验中各种方法峰值信噪比，均方误差和结构相似性的比较结果。从表中数据可以看出，文献[7,9]几乎有着同样的复原结果，而本文方法的PSNR和SSIM均有明显地提高。表2给出了各种方法达到停止标准时所需的执行时间和两步中分别所需的迭代次数。由各种方法的迭代次数可以看出，本文方法通过有效使用交替迭代以及分裂Bregman方法，使其计算复杂度大大降低，导致它的计算时间较其它两种方法要少得多，从而使其达到加速收敛的目的。

表1 各种方法的恢复图像定量指标比较

表2 各种方法达到停止标准所需的时间和两步中分别所需的迭代次数

5 结论

本文在研究LOT模型的基础上，提出了一种新的变分去噪模型。新模型由于耦合了两个变量，因此，在求解时，先利用交替极小化方法化原模型为两个简单的子模型，然后再利用分裂Bregman方法对其进行交替求解。由于两子模型对LOT模型中的两步从构成方式及计算方式上分别进行了改进，因此，数值实验表明，新方法不仅能够有效地提高恢复图像的质量，而且与文献[7]中方法相比收敛速度有明显改进。

[1]Perona P and Malik J.Scale space and edge detection using anisotropic diffusion[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1990,12(7)：629-639.

[2]Rudin L,Osher S,and Fatemi E.Nonlinear total variation based noise removal algorithms[J].Physica D,1992,60(1-4)：259-268.

[3]张伟斌,冯象初,王卫卫.图像恢复的小波域加速 Landweber迭代阈值方法[J].电子与信息学报,2011,33(2)：342-346.Zhang Wei-bin,Feng Xiang-chu,and Wang Wei-wei.Accelerated Landweber iterative thresholding algorithm in wavelet domain for image restoration[J].Journal ofElectronics＆Information Technology,2011,33(2)：342-346.

[4]武晓玥,郭宝龙,李雷达.一种新的结合非下采样 Contourlet与自适应全变差的图像去噪方法[J].电子与信息学报,2010,32(2)：360-365.Wu Xiao-yue,Guo Bao-long,and Li Lei-da.A new image denoising method conbining the nonsubsampled contourlet transform and adaptive total variation[J].Journal of Electronics＆Information Technology,2010,32(2)：360-365.

[5]张军,韦志辉.SAR图像去噪的分数阶多尺度变分PDE模型及自适应算法[J].电子与信息学报,2010,32(7)：1654-1659.Zhang Jun and Wei Zhi-hui.Fractional-order multiscale variation PDE model and adaptive algorithm for SAR image denoising[J].Journal of Electronics＆Information Technology,2010,32(7)：1654-1659.

[6]Lysaker M,Lundervold A,and Tai X C.Noise removal using fourth-order partial differential equation with applications to medical magnetic resonance images in space and time[J].IEEE Transactions on Image Processing,2003,12(12)：1579-1590.

[7]Lysaker M,Osher S,and Tai X C.Noise removal using smoothed normals and surface fitting[J].IEEE Transactions on Image Processing,2004,13(10)：1345-1357.

[8]Hahn J,Tai X C,Borok S,et al..Orientation-matching minimization for image denoising and inpainting[J].International Journal of Computer Vision,2011,92(3)：308-324.

[9]Yang Yu-fei,Pang Zhi-feng,Shi Bao-li,et al..Split Bregman method for the modified LOT model in image denoising[J].Applied Mathematics and Computation,2011,217(12)：5392-5403.

[10]Goldstein T and Osher S.The split Bregman method for L1 regularized problems[J].SIAM Journal on Imaging Sciences,2009,2(2)：323-343.

[11]Goldstein T,Bresson X,and Osher S.Geometric applications of the split Bregman method：segmentation and surface reconstruction[J].Journal of Scientific Computing,2010,45(1-3)：272-293.

[12]Wu Chun-lin and Tai X C.Augmented Lagrangian method,dual methods and split-Bregman iterations for ROF,vectorial TV and higher order models[J].SIAM Journal on Imaging Science,2010,3(3)：300-339.

[13]Cai J F,Osher S,and Shen Z W.Split Bregman methods and frame based image restoration[J].Multiscale Modeling and Simulation,2009,8(2)：337-369.

[14]孙玉宝,费选,韦志辉,等.稀疏性正则化的图像泊松恢复模型及分裂 Bregman迭代算法[J].自动化学报,2010,36(11)：1512-1519.Sun Yu-bao,Fei Xuan,Wei Zhi-hui,et al..Image restoration model under poisson noise using sparse representations and split Bregman iteration algorithm[J].Acta Automatica Sinica,2010,36(11)：1512-1519.