基于全局最优的快速一致性点漂移算法

赵 键 孙即祥 周石琳 李智勇 王亮亮

(国防科学技术大学电子科学与工程学院 长沙 410073)

1 引言

点模式(或称点集)匹配广泛应用于图像配准[1]，图像分类[2]与检索[3]，目标识别[4]，形状匹配[5]和立体视觉[6]等领域。其任务是寻找点集之间的对应关系和求解点集之间的变换关系，但由于形变、噪声、出格点以及缺失点等因素的影响始终难以完全解决，因而研究有效且鲁棒的点模式匹配算法已经成为目前模式识别和机器视觉等领域的研究热点之一。目前，点模式匹配算法大致可以分为两大类，一是基于变换关系求解的算法，是通过估计点模式之间的空间变换参数，利用该参数恢复或模拟点模式间的变换，从而求解点模式匹配问题，也称之为基于变换参数估计的算法。这类算法主要有一致性点漂移算法[7]，迭代最近点算法[8]，基于薄板样条的鲁棒点模式匹配算法[9]，等。二是基于匹配关系求解的算法，是通过提取点集中点的特征而后运用匹配识别方法获得点模式间的匹配关系，从而求解点模式匹配问题，或更形象地称为基于特征的匹配算法。这类算法主要有基于形状上下文的方法[10]，基于不变量特征的方法[11]以及基于谱图论的方法[12]等。

迭代最近点(Iterative Closest Point,ICP)算法[8]构造简单、计算复杂度低，是应用广泛的点集匹配算法之一。ICP算法的基本思想是：基于最近距离准则，通过指派点集间点与点的对应关系，求解点集间的变换模型。然后，再通过估计的变换模型来重新确定对应关系，如此迭代达到局部最小值。尽管ICP算法直观简洁，但其对于点集间的初始化校准以及点集中所存在的出格点、缺失点较为敏感。基于薄板样条的鲁棒点模式匹配算法(TPS-RPM)算法[9]通过结合软指派方法和确定性退火机制，来迭代的估计变换关系和更新对应关系。相比于ICP算法，TPS-RPM不仅适用于非刚体变换，而且其对于噪声、出格点的鲁棒性更强。尽管采用了确定性退火机制来避免陷入部分局部最优解，但是TPS-RPM算法也无法保证能达到全局最优，而且其迭代速度较慢。基于谱图论的方法是一类利用邻接矩阵或者与其密切相关的Laplace矩阵的特征值和特征矢量来刻画点集全局结构的方法[12]。经典谱图论方法的显著优点是构造简单、计算量小，但由于它们是精确点模式匹配算法，因此，若待匹配的两个点集大小不同以及存在位置噪声时性能较差。基于形状上下文的算法[10]要求点集间对应点的邻域结构保持相似，而基于不变量特征的方法[11]则需要保持点集的凸壳结构保持不变，因而它们均对于噪声、出格点以及遮挡导致的缺失点等情况鲁棒性较差。

一致性点漂移算法[7](Coherent Point Drift,CPD)是一种鲁棒的基于高斯混合模型的点集匹配算法。该算法适用于刚体以及非刚体变换下的多维点集配准问题，对于噪声、出格点以及缺失点的影响具有较强鲁棒性。但由于采用的是EM算法框架，其存在两个缺陷：(1)对于迭代的初始点选取十分敏感，如果选取不当，极易陷入局部最优解，从而导致算法的最终匹配结果较差；(2)CPD算法的收敛速度与待匹配点集大小成反比，从而导致在解决大规模点集匹配问题时，该算法的运行速度较慢。针对上述问题，本文提出了基于全局最优的快速一致性点漂移算法(Global Optimal ＆ Fast CPD,GOFCPD)。本文首先将待匹配点集进行正交标准形约简，再证明当初始旋转角度与真实旋转角度间隔小于π/4以及高斯混合模型中协方差等于点集间均方距离时，EM算法迭代能达到全局最优。基于上述结论，本文采取多重初始化EM算法策略，实现了全局优化。针对单重初始化CPD算法的收敛速度随点集大小增大而减小以及在全局优化时所采用的多重初始化所带来的计算复杂度成倍数增加的问题，本文提出了基于置信域的全局收敛平方迭代期望最大化(TR-gSQUAREM)算法，从而最终实现超线性的收敛速度。

2 基于全局最优的快速一致性点漂移算法(GOF-CPD)

本节首先对原始的一致性点漂移算法(CPD)进行简单介绍，然后提出点集的正交标准形约简方法，利用约简后点集的重要性质，证明在高斯混合模型参数最大似然估计问题中，不完全观测数据的对数似然函数在约简后参数空间中的全局最优解附近区域是凸函数，并给出了该区域的边界值，再以凸区域边界值作为多重初始点来达到全局最优。最后，为实现快速的全局最优算法，提出基于置信域的二次迭代EM算法来取代原始EM算法框架。

2.1 一致性点漂移算法(CPD)

一致性点漂移算法(CPD)本质上是将点集配准过程转化为高斯混合模型(Gaussian Mixture Model,GMM)概率密度函数的参数估计问题[7]。其中，将模板点集中各点视作高斯混合模型中各个高斯分量质心，而目标点集则代表了混合模型所生成的观测样本数据。通过观测数据的对数似然函数最大化将GMM质心拟合至目标点集中的对应点。在最优情况下，不仅实现了点集之间的配准，而且通过GMM中高斯成分的后验概率得到了点集之间的匹配对应关系。在点集配准过程中，CPD算法将模板点集作为整体按一定的变换关系向目标点集进行保持拓扑结构一致性的漂移运动。

设YM×D=[y1,y2,…,yM]T为模板点集，XN×D=[x1,x2,…,xN]T为目标点集，其中M为模板点集大小，N为数据点集大小，D为点的维数。以模板点集中各点作为各个混合高斯成分质心而组成高斯混合模型，定义该GMM的概率密度函数为

将GMM的各个高斯分量质心按变换参数集φ进行几何变换，同时其协方差σ2也随之变化。设GMM总的参数集为Θ=(φ,σ2)，匹配关系可用后验概率矩阵来定义P=[P(m|xn)]M×N。最后，通过极大化不完全观测数据的对数似然函数L(Θ)来估计参数集Θ和P：

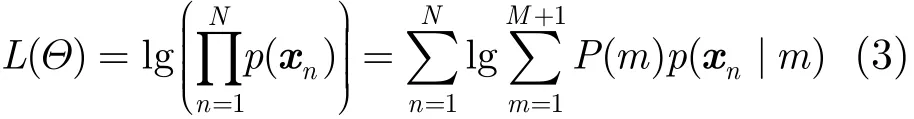
CPD算法采用了期望最大化(EM)算法来求解式(3)的极大化问题，即分别以求期望值(E-步)和求最大值(M-步)两步进行迭代循环来分别求解P和Θ。虽然EM算法能收敛到对数似然函数的稳定点，但是不能保证收敛到全局极大值点。因此，CPD算法本质上是一种局部最优算法，其对于初始点的选取十分敏感。

2.2 点集的正交标准形约简

本文主要讨论的是一般仿射变换下2维点集匹配的问题，相比于刚体和相似变换，仿射变换更具一般性，但由于仿射变换参数空间维数较高(6个自由度)，从而导致全局寻优的过程较为复杂。因此，本文首先将点集进行正交标准形约简，将一般仿射变换问题约简为仅有旋转的刚体变换问题。

设模板和目标点集的维数D=2。不失一般性，首先考虑精确点集(待匹配点集中点的数目相同且一一对应)的匹配问题，则正交标准形约简分为以下3 步：

原始点集经过上述约简后所得到的正交标准形具有如下4个重要的性质：

性质 1 正交标准形的二阶矩矩阵为单位阵，即有：YT⋅Y=I,XT⋅X=I，其中I为单位矩阵；

性质 4 存在一般仿射变换关系的原始点集在经过上述正交标准形约简后，所得到的正交标准形之间仅存在旋转变换关系。即：设原始点集X和Y之间存在一般仿射变换关系：X=Y⋅+1N×1在分别进行了正交标准形约简后得到X′和Y′，两者仅存在旋转变换关系：

由性质4可知，经过正交标准形约简后的精确点集之间所存在的一般仿射变换可被约简为正交旋转变换，即此时仿射变换参数集φ={a11,a12,a21,a22,tx,ty}简化为φ={θ}。

需要特别说明的是：上述性质是在精确点集匹配问题中成立，而当点集中存在出格点、缺失点以及噪声时，也即在非精确点集匹配问题中，两个存在仿射变换关系的点集，在经过了正交标准形约简后，它们之间仍然保持仿射变换关系。此时，可将仿射变换矩阵AY′X′进行SVD分解[13]：

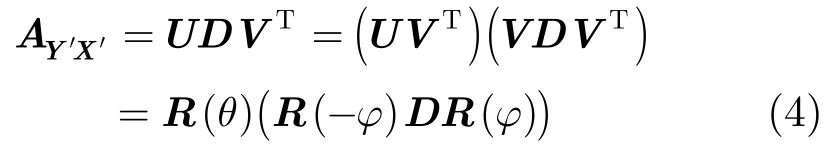
2.3不完全观测数据对数似然函数的全局极值附近凸区域边界

Wu[14]证明了在局部极值附近区域，如果对数似然函数是凸函数时，EM算法保证能收敛到该局部极值。因此，本节将确定对数似然函数的全局极值附近凸区域及其边界值范围。

设正交约简后的精确模板与目标点集分别为Y和X。则由第2.2小节可知，此时两者存在正交旋转变换：X=Y⋅RT(θ*),θ*为真实旋转角度(也即全局最优解)。因此，可将xn在第m个高斯分量中的概率密度p(xn|m)用 Δθ=(θ-θ*)来表示：

由式(3)和式(5)可得到不完全观测数据的对数似然函数关于Δθ以及σ2的偏导数分别为

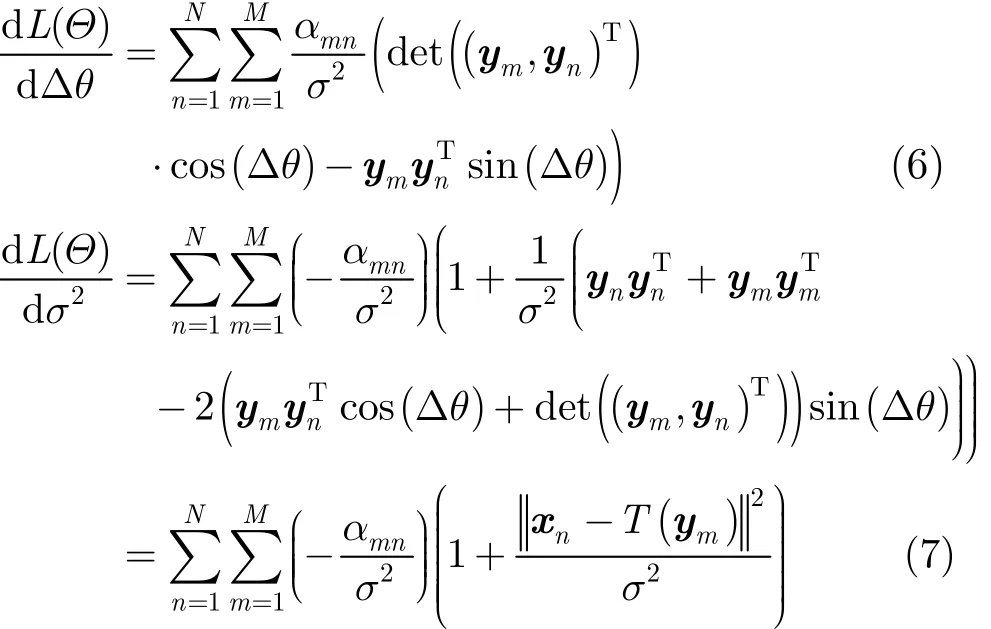
式(6)和式(7)中的

通过式(6)，式(7)以及2.2小节中4个性质可得到下面的推论1。

推论1 在精确点集匹配情况下时，取2σ=则有当M→+∞，在其中θ*为真实的旋转角度。

由推论1可知，与真实旋转角度θ*间隔π/4的θ为对数似然函数L(Θ)在角度参数维上的驻点，又由式(7)可知，对于任意的σ2均满足因此，真实解Θ*={θ*,0}附近的凸区域边界值可设为：

图1(a)为500个随机模板点集以及由该模板经过随机仿射变换所生成的目标点集所构成的不完全观测数据对数似然函数的3维曲面图，其X轴为相对于真实旋转角度的角度间隔,∈[- 1 80°,180°],Y轴为GMM的协方差σ2,σ2∈[0,2/500],Z轴为对数似然函数值L(Θ)。从图1(a)中可看出，Δθ=0°,σ2=0 为全局最优解，在该全局最优解附近L(Θ)呈现出凸函数特性，为了更直观显示出该凸区域的边界，现将L(Θ)转化为2维平面曲线图。如图1(b)所示，图中X轴为Δθ,Y轴为L(Θ)，而每条曲线表示在某一固定的σ2下的对数似然函数随角度间隔变化的曲线，其中位于最下方的曲线其协方差σ2=2 /M=2 /500，随着σ2的减少，曲线也逐渐向上分布即L(Θ)逐渐增大，也进一步证明了dL(Θ)/dσ2＜0的正确性，从图1(b)可知，当取σ2=2/M时，Δθ=± 4 5°为该曲线离真实解Δθ=0°附近最近的驻点，因此以这两个驻点作为真实解附近凸区域的边界值也是正确直观的。

2.4 基于全局最优的快速CPD算法

由第2.3小节可知，对数似然函数的真实解附近凸区域边界值可以确定下来，而当初始点位于真实解附近的凸区域内时，EM算法能确保最终收敛于该真实解[15]。因此，本文采用基于多重初始化的策略来实现CPD算法的全局优化，从而提出了基于全局最优的CPD算法(Global Optimal CPD,GOCPD)。GO-CPD算法核心在于如何选取多个初始点：首先由推论1可知，为了能达到全局最优，初始旋转角度与真实旋转角度之间的间隔不能大于45°，也即初始点的旋转角度之间的间隔不能大于90°，由此可知，初始点的个数至少为4。设4个初始点的集其中第i个初始点其中初始角度其余的参数为：=2 /M。然后，在4个初始点下各自执行EM迭代循环直至收敛。最后比较所得到的4个对数似然函数的局部极值L={L(i)(Θ)=1,2,3,4}，以其中最大值所对应的解作为最终的全局最优解：Θ*=argmax(L)。

上述的GO-CPD算法虽能达到全局最优，但其所采用的是原始EM算法求解似然函数极值，而原始EM算法收敛速度与缺失数据信息量是成反比的[15]，因此随着点集大小的增加，原始EM算法的收敛速度也会随之迅速下降。此外，GO-CPD算法需要进行多重初始化下的EM迭代循环，因此算法总的迭代次数会随着点集大小的增加而成倍增加。考虑到算法的效率问题，须对GO-CPD算法进行加速，本文拟对其单重初始化中的原始EM算法进行加速。

文献[16]提出了基于平方迭代的加速EM(SQUAREM)算法，该算法是一种简单的、全局收敛的EM加速算法，在保持原始EM算法的单调性基础上，又结合数值外推方法达到超线性的收敛速度。其基本原理是：将原始EM算法定义为参数空间上Θ的不动点映射F，即F：Θ↦Θ，则原始EM算法的迭代过程可表示为

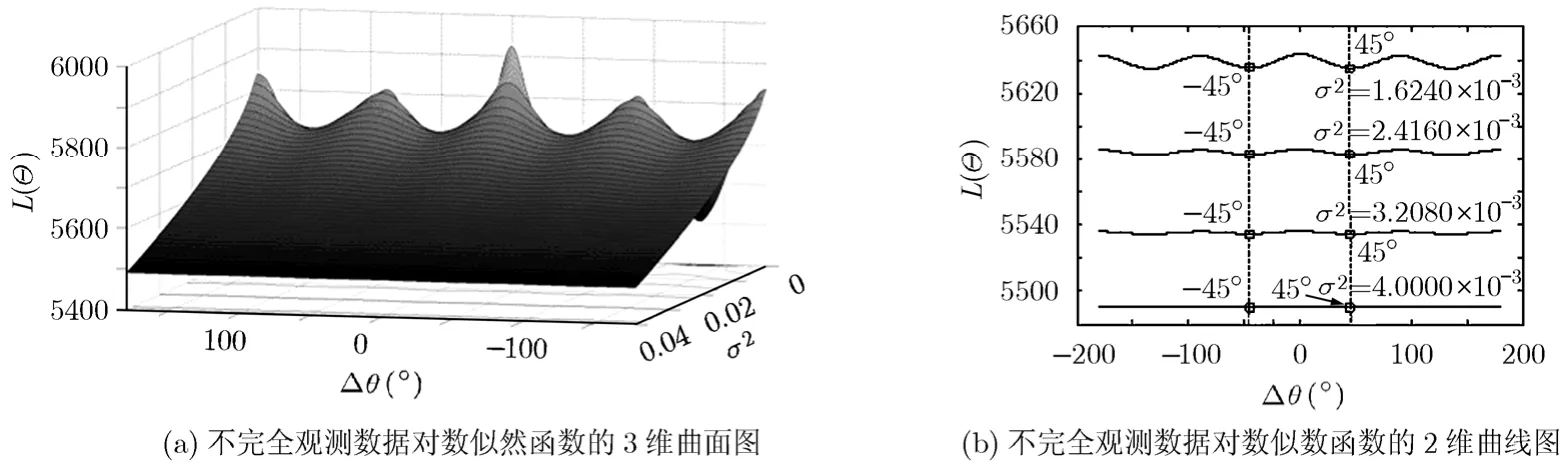
图1 不完全观测数据对数似然函数的3维曲面图和2维曲线图

相比于传统的Newton方法以及Steffensen方法[16]，SQUAREM算法利用迭代误差的平方来近似迭代的步长和方向，从而得到其迭代公式为

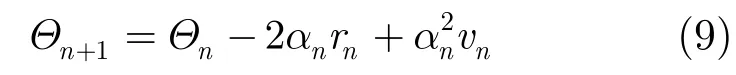
其中αn,rn和vn的定义为

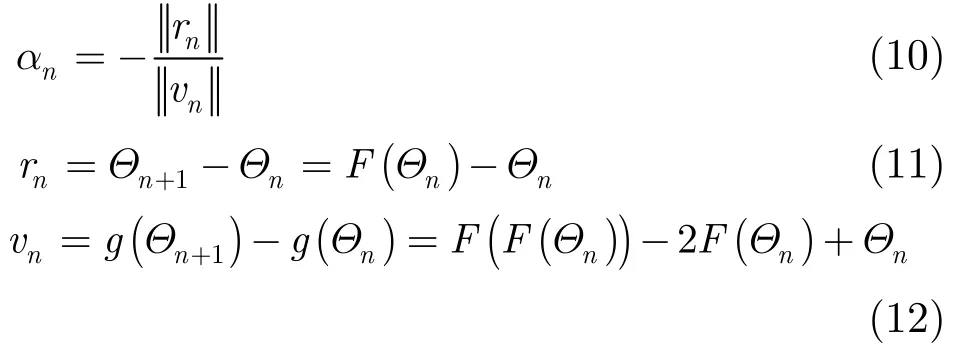
式(12)中的g(Θn)为F在Θn处的梯度：g (Θn)=F(Θn)-Θn。

当初始点远离局部极值点时，SQUAREM并不能保证最终收敛于该局部极值点，为了达到全局收敛性，文献[16]提出了SQUAREM的全局收敛方法(gSQUAREM)，其核心思想为：当α＞-1时，即SQUAREM算法迭代中的对数似然函数不满足单调递增时，需要通过回溯方法来自适应调整步长使α=-1(即恢复原始EM算法迭代)；反之，当α＜-1时，则不需要调整步长α。因此，gSQUAREM既能保持对数似然函数单调递增，又能进一步提高收敛速度。

在实际应用中，上述gSQUAREM虽然能保证在似然函数递增的方向上收敛，却极有可能“舍近求远”地收敛至离初始点较远的局部极值，从而导致其最终不能收敛至真正的全局最优解。为克服上述缺陷，结合第2.3小节中的凸区域边界值，本文提出了基于置信域的全局收敛平方迭代EM算法(Trust Region gSQUAREM,TR-gSQUAREM)，并将其替换GO-CPD算法中的原始EM算法，最终形成了基于全局优化的快速CPD算法(Global Optimal ＆ Fast CPD,GOF-CPD)。GOF-CPD算法的具体流程如表1 所示。

表1 GOF-CPD算法流程

3 实验结果与分析

本节进行了模拟仿真和真实数据两种实验。在模拟仿真实验中，首先在刚体变换下验证了本文算法的全局寻优能力，再将本文算法与其他几种算法分别进行了抗噪声和抗出格点以及抗缺失点能力的比较。在真实图像数据实验中则验证了本文算法解决实际图像特征点匹配问题的能力。

3.1 模拟仿真实验

模拟点集数据的生成方式为：模板点集Y为在单位平面内服从均匀分布的随机点模式，其大小为M。目标点集X是由Y经过随机的仿射变换后产生的，两者大小相同即N=M，本文称Y与X分别为精确模板点集和精确目标点集。加噪声的非精确点集Yn与Xn是分别在精确点集Y与X内每个点位置上叠加高斯噪声，其均值为零，标准差为精确点集内任意两点之间最小欧式距离的f倍(本文称f为噪声水平因子)。加出格点的非精确点集Yo和Xo则是分别在精确目标点集所在区域内随机增加Ro⋅M和Ro⋅N个点后所构成的点集(本文称Ro为出格点比率)。存在缺失点的非精确点集Ym和Xm则是分别在精确点集中随机减少Rm⋅M和Rm⋅N个点后所构成的点集(本文称Rm为缺失点比率)。每组模拟仿真实验均进行了100次蒙特卡洛实验，所采用的实验平台为：Pentium Dual-Core CPU 2.93G，内存2.0 G。

3.1.1 算法全局优化能力比较实验下面将本文所提出的GOF-CPD算法与CPD算法[7]，ICP算法[8]和TPS-RPM 算法[9]进行了在仅存在旋转的刚体变换下各种算法的全局优化能力比较实验，即令180°，其中模板点集与目标点集均为模拟的精确点集，点集大小均为400。图2给出了4种算法的正确匹配率Pc随旋转角度θ的变化曲线，从图2可看出，ICP算法仅在[- 1 5°,15°]小角度范围内能保持较高的正确匹配率，CPD算法只能在[-4 5°,45°]范围内达到85%以上的匹配正确率，TPS-RPM算法在[-4 5°,45°]内达到98%以上的匹配正确率。而本文的GOF-CPD算法能在[- 1 80°,180°]的全角度区间内保持100%的匹配正确率，从而验证了本文算法具备全局优化的能力。

3.1.2 算法鲁棒性比较实验将本文算法与其他3种算法分别进行了鲁棒性的综合比较实验，即：抗噪声和抗出格点以及抗缺失点能力的综合比较。

其中精确模拟点集之间的随机仿射变换参数分别是在 - 180°≤θ,φ≤180°,0.1 ≤λx,λy≤ 1 0,-5≤tx,ty≤ 5 范围内服从均匀分布的随机值，而精确点集大小取为：N=M=3 0。每种鲁棒性实验中分成两组进行统计实验：第1组为非精确模板点集与精确目标点集之间的匹配；第2组则为精确模板点集与非精确目标点集之间的匹配。

在上述的非精确模板点集与精确目标点集的匹配实验中，鲁棒性权值设为ω=0；而在精确模板点集与非精确目标点集的匹配实验中，鲁棒性权值设为ω=0.5。从图3和图4可知，在随机仿射变换下，本文的GOF-CPD算法对于噪声、出格点以及缺失点的鲁棒性均要明显强于其他3种算法。

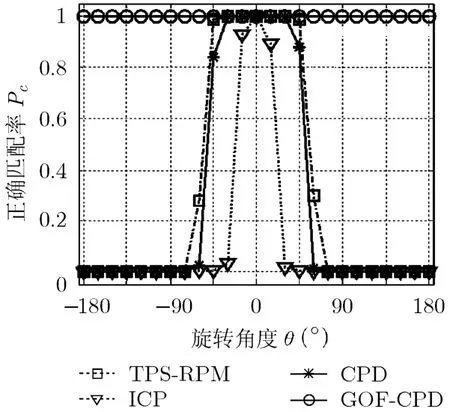
图2 不同算法在刚体旋转变换下的全局优化能力比较实验结果

3.1.3 算法时间复杂度比较实验将本文算法与其他几种算法进行了算法平均耗时的比较实验，其中模拟点集之间仿射变换参数分别是在 - 1 80° ≤θ,φ≤ 1 80°,0.1 ≤λx,λy≤ 1 0,- 5 ≤tx,ty≤ 5 范围内服从均匀分布的随机值，而模板与目标点集均为精确点集，点集大小取值满足：{M=N=10⋅ 2i-1|i=1,2,…,8 }。

从图5(a)可看出，本文的GOF-CPD算法在点集大小少于160时，其平均耗时比CPD算法稍多，但是当点集大小多于160后，两者之间的平均耗时则相差无几，而从图5(b)中可知，本文的GOF-CPD算法要比CPD算法的平均迭代次数少，而且随着点集大小的增加呈现出超线性的收敛速度；GO-CPD算法无论从平均耗时还是平均迭代次数上都明显多于本文的GOF-CPD算法；而ICP和TPS-RPM算法的平均耗时也要多于本文算法。

3.2 真实图像数据实验结果

为了验证GOF-CPD算法解决实际图像特征点匹配问题的能力，本文采用了两幅从不同视角拍摄的建筑物图像进行实验，如图6(a),6(b)所示，两幅图像之间存在一定的仿射变换关系。首先在两幅图像中各自提取Harris角点，模板与目标图像中所提取的Harris角点分别用圆圈和十字符号表示，其中模板图像中有347个角点，而目标图像中有393个角点。图6(c)为配准前的模板点集与目标点集。本文GOF-CPD算法的最终匹配结果为303对匹配点(鲁棒性权值设为ω=0.5)，图6(d)给出了本文算法的最终配准结果。可见当模板和目标点集中均存在较多的出格点、缺失点以及较强的噪声时，本文算法能达到较高的匹配正确率。相比之下，由于点集间存在着较大的仿射旋转角度从而导致CPD算法，TPS-RPM 算法，ICP算法在上述真实复杂情况下均匹配失效。

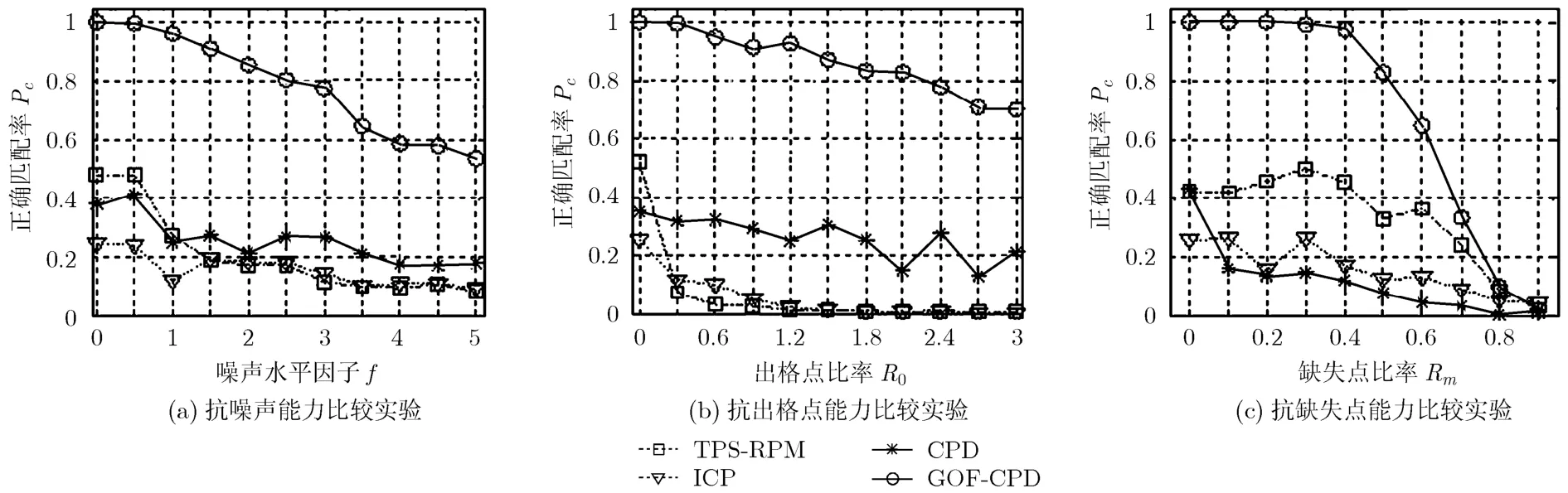
图3 非精确模板点集与精确目标点集匹配情况下算法鲁棒性统计比较实验结果 (ω=0)

图4 精确模板点集与非精确目标点集匹配情况下算法鲁棒性统计比较实验结果 (ω=0.5)

图5 不同算法平均耗时以及平均迭代次数统计比较实验结果

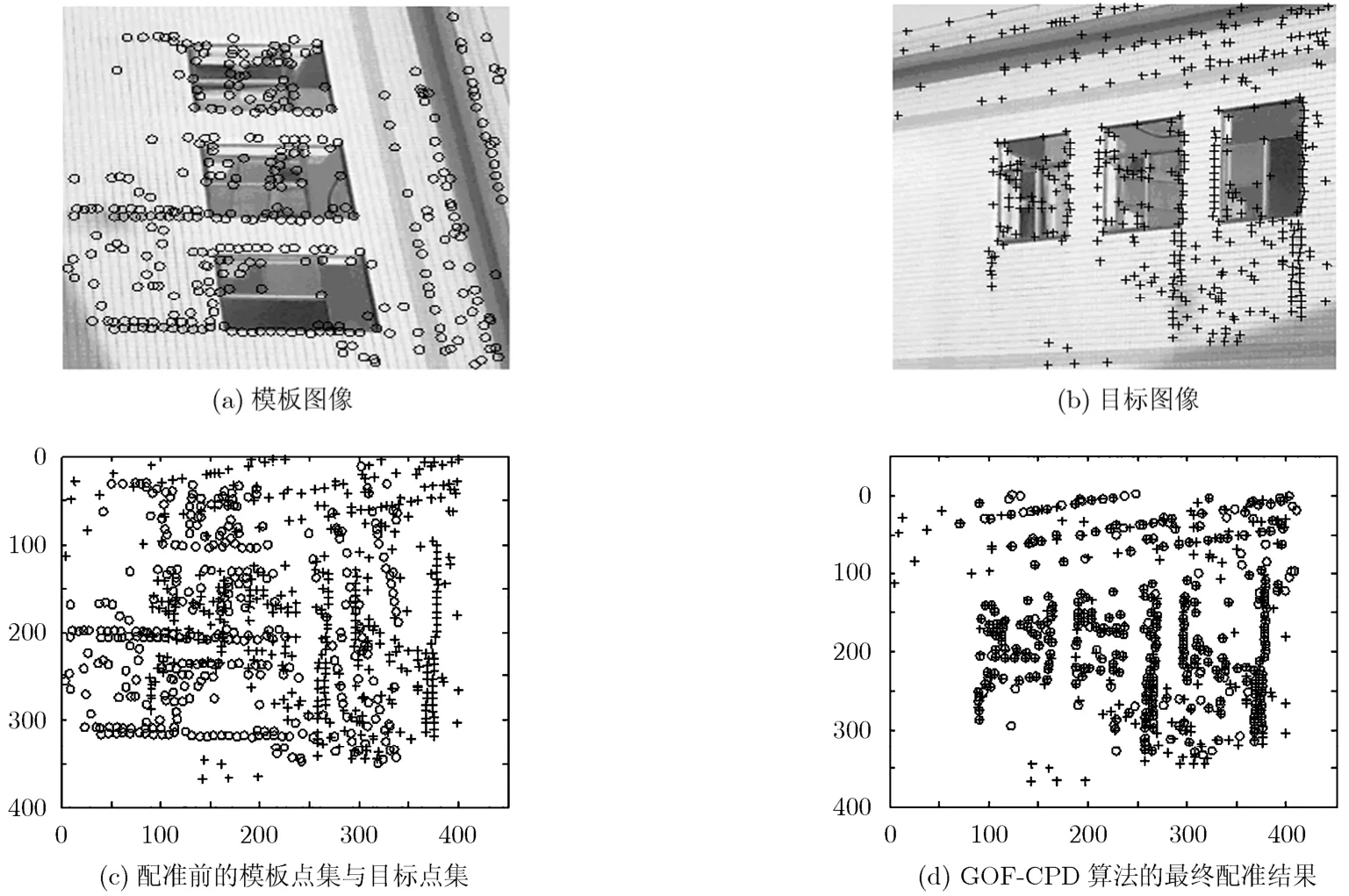
图6 真实图像数据下本文GOF-CPD算法的匹配结果示意图

4 结论

一致性点漂移算法[7]对于初始点的设置十分敏感，仅能达到局部最优，而且算法的收敛速度随着点集大小增加而下降较快。针对这些问题，本文提出了一种新的点模式匹配算法基于全局最优的快速一致性点漂移算法。首先，提出了点集的正交标准形约简方法，利用约简后点集的重要性质，证明了在高斯混合模型参数最大似然估计问题中，不完全观测数据的对数似然函数在约简后参数空间中的全局最优解附近区域是凸函数，并给出了该区域的边界值，再以凸区域边界值作为多重初始点来达到全局最优。最后，为实现快速的全局最优算法，提出了基于置信域的二次迭代EM算法来取代原始EM 算法框架。模拟仿真与真实数据实验验证了在仿射变换下本文算法的全局最优性以及对于噪声、出格点以及缺失点均有较强的鲁棒性。

[1]Jackson B P and Goshtasby A A.Registering aerial video images using the projective constraint[J].IEEE Transactions on Image Processing,2010,19(3)：795-804.

[2]Nasreddine K,Benzinou A,and Fablet R.Variational shape matching for shape classification and retrieval[J].Pattern Recognition Letters,2010,31(12)：1650-1657.

[3]Jamieson M,Fazly A,Stevenson S,et al..Using language to learn structured appearance models for image annotation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2010,32(1)：148-164.

[4]Baloch S and Krim H.Object recognition through topo-geometric shape models using error-tolerant subgraph isomorphisms[J].IEEE Transactions on Image Processing,2010,19(5)：1191-1200.

[5]Noma A,Pardo A,and Roberto M.Structural matching of 2D electrophoresis gels using deformed graphs[J].Pattern Recognition Letters,2011,32(1)：3-11.

[6]McKeon R T and Flynn P J.Three-dimensional facial imaging using a Static Light Screen (SLS)and a dynamic subject[J].IEEE Transactions on Instrumentation and Measurement,2010,59(4)：774-783.

[7]Myronenko A and Song X B.Point-set registration：coherent point drift[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2010,32(12)：2262-2275.

[8]Besl P J and Mckay N D.A method for registration of 3-D shapes[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1992,14(2)：239-256.

[9]Chui H and Rangarajan A.A new point matching algorithm for non-rigid registration[J].Computer Vision and Image Understanding,2003,89(2)：114-141.

[10]Belongie S,Malik J,and Puzicha J.Shape matching and object recognition using shape contexts[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24(4)：509-522.

[11]Gope C and Kehtarnavaz N.Affine invariant comparison of point-sets using convex hulls and hausdorff distances[J].Pattern Recognition,2007,40(1)：309-320.

[12]Caetano T S,McAuley J J,Cheng L,et al..Learning graph matching[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2009,31(6)：1048-1058.

[13]Hartley R and Zisserman A.Multiple View Geometry in Computer Vision[M].Second Edition,Cambridge：UK,Cambridge University Press,2004：39-40.

[14]Wu C F J.On the convergence properties of the EM algorithm[J].The Annals of Statistics,1983,11(1)：95-103.

[15]Ma J W,Xu L,and Jordan M I.Asymptotic convergence rate of the EM algorithm for gaussian mixtures[J].Neural Computation,2000,12(2)：2881-2907.

[16]Varadhan R and Roland C.Simple and globally convergent methods for accelerating the convergence of any EM algorithm[J].Scandinavian Journal of Statistics,2008,35(1)：335-353.