水下爆炸冲击荷载作用下混凝土重力坝的破坏模式＊

张社荣，王高辉，王 超，孙 博

（天津大学水利工程仿真与安全国家重点实验室，天津 300072）

坝工抗爆问题一直是坝工安全必须考虑的重要问题之一。随着坝工技术的发展，高坝（100～300m）建设进入快速发展阶段。大坝一旦失事，将造成巨大的人员伤亡和经济损失。因此，开展大坝在爆炸冲击荷载作用下的动力响应和破坏模式分析，具有非常重要的意义。

水下爆炸属于多相耦合的交叉学科，由于它的复杂性，研究一直以实验为主［1－2］。近年来，随着计算机技术及实验手段的不断进步，有关水下爆炸的理论、实验和数值模拟研究快速发展；尤其，随着计算机硬件及计算方法的逐步完善，数值模拟水下爆炸对结构的响应成为可能，如：徐俊祥等［3］建立了水下爆炸的全耦合模型分析大坝的动力响应；李本平等［4］对制导炸弹在坝前水面爆炸的大坝破坏效应进行了分析。但由于问题的复杂性，关于水下爆炸冲击荷载作用下大坝破坏模式及其失事机理的研究很少。

本文中，采用非线性显式动力分析程序LS－DYNA，建立重力坝水下爆炸全耦合模型，对大坝在水下爆炸冲击荷载作用下的动力响应进行全性能数值模拟，分析大坝在水下爆炸冲击荷载作用下的破坏模式及抗爆性能，为混凝土重力坝的抗爆设计和防护提供理论参考。

1 材料模型及状态方程

1.1 混凝土本构模型

混凝土材料在爆炸高加载率荷载作用下，应变率高达10～103s－1［5］，强度有显著提高，抗压强度能够提高到2倍，抗拉强度甚至能提高到7倍［5－6］。Holmquist－Johnson－Cook（HJC）本构模型［7］是针对混凝土材料的一种率相关损伤型本构模型，综合考虑了混凝土的大应变、高应变率、高压效应，能很好地描述高应变率条件下混凝土的响应问题，主要包括屈服方程、损伤演化方程、状态方程。HJC模型的屈服面如图1（a）所示，可表述为［8］

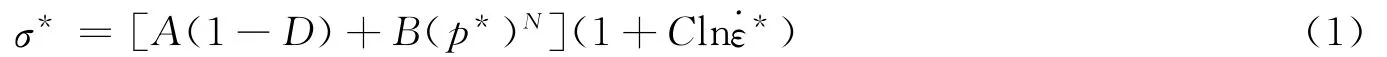
式中：σ＊＝σ／f′c，p＊＝p／f′c，σ为实际等效应力，p为静水压力，f′c为材料的静态抗压强度为真实应变率为参考应变率；D为损伤度，0≤D≤1；A、B、N、C为材料的强度参数，A表示标准化的凝聚力强度，B表示标准化的压力硬化系数，C是应变率系数。

材料的损伤累积破坏可用损伤度D表示，损伤累积考虑了等效塑性应变、塑性体积应变和静水压力的影响。损伤演化方程可以表示为［8］

式中：Δεp和Δμp分别为一个计算循环内的等效塑性应变和塑性体积应变和分别为常压下破碎的等效塑性应变和塑性体积应变。损伤常数是混凝土材料允许的最小塑性应变，且（D1和D2为混凝土材料的损伤常数），如图1（b）所示。由于混凝土在压缩过程中内部孔隙不断崩塌，导致凝聚力强度的丧失，因此在大多数情况下，混凝土的损伤主要来自塑性体积应变。

HJC模型采用状态方程描述静水压力与体积应变之间的关系。在体积应变已知的情况下，可通过状态方程计算相应的静水压力。混凝土的状态方程分三段表述［8］，如图1（c）所示。第一阶段（见图1（c）中OA）是线弹性阶段，静水压力和体积应变满足线性关系K＝p／μ，其中K为体积弹性模量，pc和μc分别为压垮的静水压力和体积应变。第二阶段（见图1（c）中AB）是过渡阶段，混凝土材料内的空洞逐渐被压缩，产生塑性变形。假设曲线仍然具有线性关系，该阶段内任意点卸载的弹性体积模量可由两端模量插值计算得到。第三阶段（见图1（c）中BC）为完全密实阶段，当压力达到pl，混凝土内部气孔被完全压碎，曲线关系常用三次多项式表示。

图1 混凝土材料模型Fig.1 The material model of the concrete

混凝土 HJC本构模型材料参数分别为［7］：ρ＝2.4t／m3，G＝14.86GPa，A＝0.79，B＝1.60，C＝0.007，N＝0.61，f′c＝48MPa，T＝4MPa，ε0＝1＝0.01＝7，pc＝16MPa，μc＝0.001，pl＝800MPa，μl＝0.1，D1＝0.04，D2＝1.0，K1＝85MPa，K2＝－171MPa，K3＝208MPa。

1.2 爆轰产物状态方程

制导炸弹质量W＝2 130kg，弹长L＝5.84m，弹径D＝370mm，装药Q＝306kg［9］。高能炸药采用高能炸药材料模型，并用JWL状态方程［10］描述

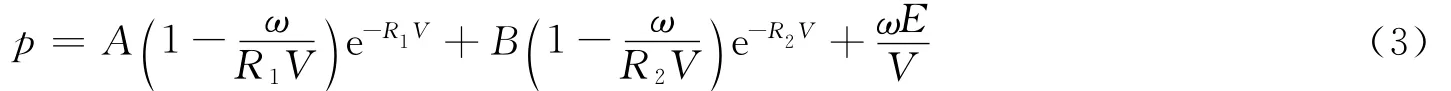
式中：p为爆轰压力；E为爆轰产物的体积内能；V为爆轰产物的相对体积（即爆轰产物体积和炸药初始体积之比）；A、B、R1、R2、ω 为特征参数，各参数取值如下：ρ＝1.86t／m3，D＝8.862km／s，pCJ＝36.8GPa，A＝934.77GPa，B＝12.723GPa，R1＝4.6，R2＝1.10，A＝9.3477×1011，ω＝0.37，E0＝9.50GJ／m3，V0＝1.00。

1.3 水状态方程

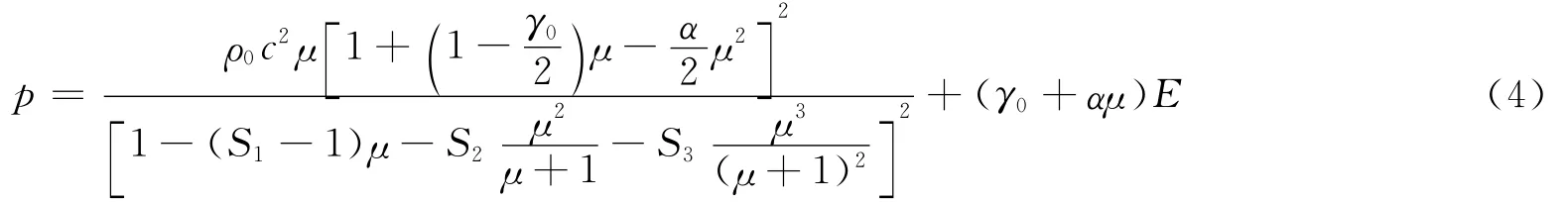
高压下的水体一般采用Grüneisen状态方程［10］描述。该状态方程用于定义压缩材料压力和体积的关系，一般形式为式中：p为爆轰压力；c、S1、S2、S3为常数；ρ0为初始密度；γ0为 Grüneisen系数；α为对γ0的一阶体积修正。各参数分别为：ρ0＝998.21kg／m3，c＝1.647km／s，S1＝1.921，S2＝－0.096，S3＝0，γ0＝0.35，E＝2.895，V0＝1.00。

1.4 空气状态方程

空气采用Mat－Null材料模型和线性多项式状态方程［10］描述，表达式为

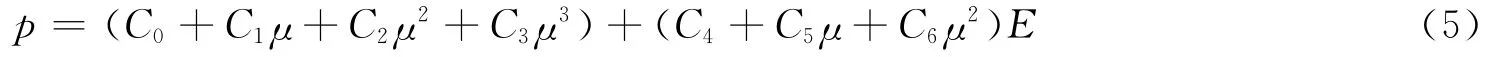
式中：μ＝ρ／ρ0－1，C0～C6为状态方程参数，V0为相对体积，E 为体积内能。取ρ0＝1.293 9kg／m3，C0＝C1＝C2＝C3＝C6＝0，C4＝C5＝0.4，V0＝1，E＝2.35MJ／m3。

2 混凝土重力坝破坏模式分析

2.1 水下爆炸全耦合模型的建立

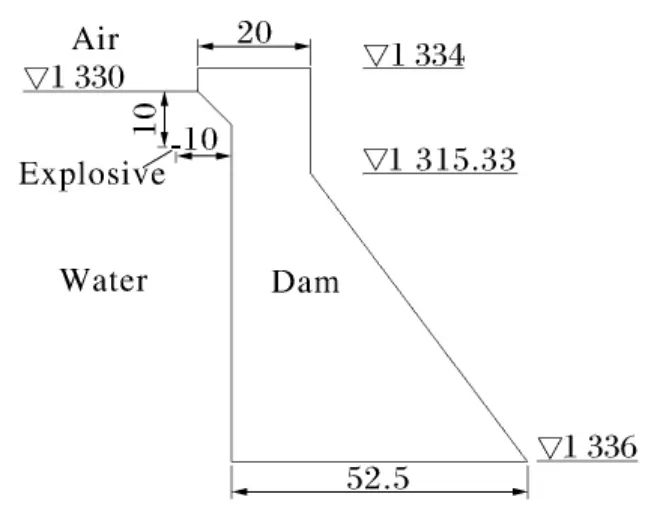
图2 水下爆炸计算示意图Fig.2 Calculation of the regional

图3 有限元计算模型Fig.3 Finite element model

重力坝主要依靠坝体自重维持稳定，下部结构体积较大，上部结构薄弱，本文中主要研究浅水近场爆炸冲击荷载作用下的大坝破坏模式。计算区域如图2所示，有限元计算模型如图3所示。模型包括大坝、高能炸药、库水、空气四种物质的耦合。其中高能炸药、库水、空气采用Euler网格建模，单元使用多物质ALE算法，大坝采用Lagrange网格建模，库水与大坝之间采用流固耦合算法。

边界条件：大坝底部施加全约束，并在边界上定义无反射边界条件，使人工边界上无应力波反射；除库水、空气与坝体交接处，库水和空气其他面均定义无反射边界条件，以此模拟库水和空气的无限区域。

材料破坏失效准则：为了研究大坝混凝土的断裂破坏，引入混凝土断裂条件，当拉伸应变达到0.002时，认为混凝土断裂失效［11］。

2.2 全性能数值模拟的工况设计

为探讨各种因素对大坝破坏模式及抗爆性能影响，进行了工况设计，见表1。选取的敏感性分析因素主要有：炸弹起爆的水下深度h、起爆点至坝上游面的距离（爆心距）R及炸弹药量Q。

高能炸弹药量306kg时采用条柱型炸药，其他炸弹药量下炸弹均按体积简化等效成立方体炸药。计算中取模型1／2为研究对象，假定起爆点在炸弹几何中心，采用单点起爆方式。

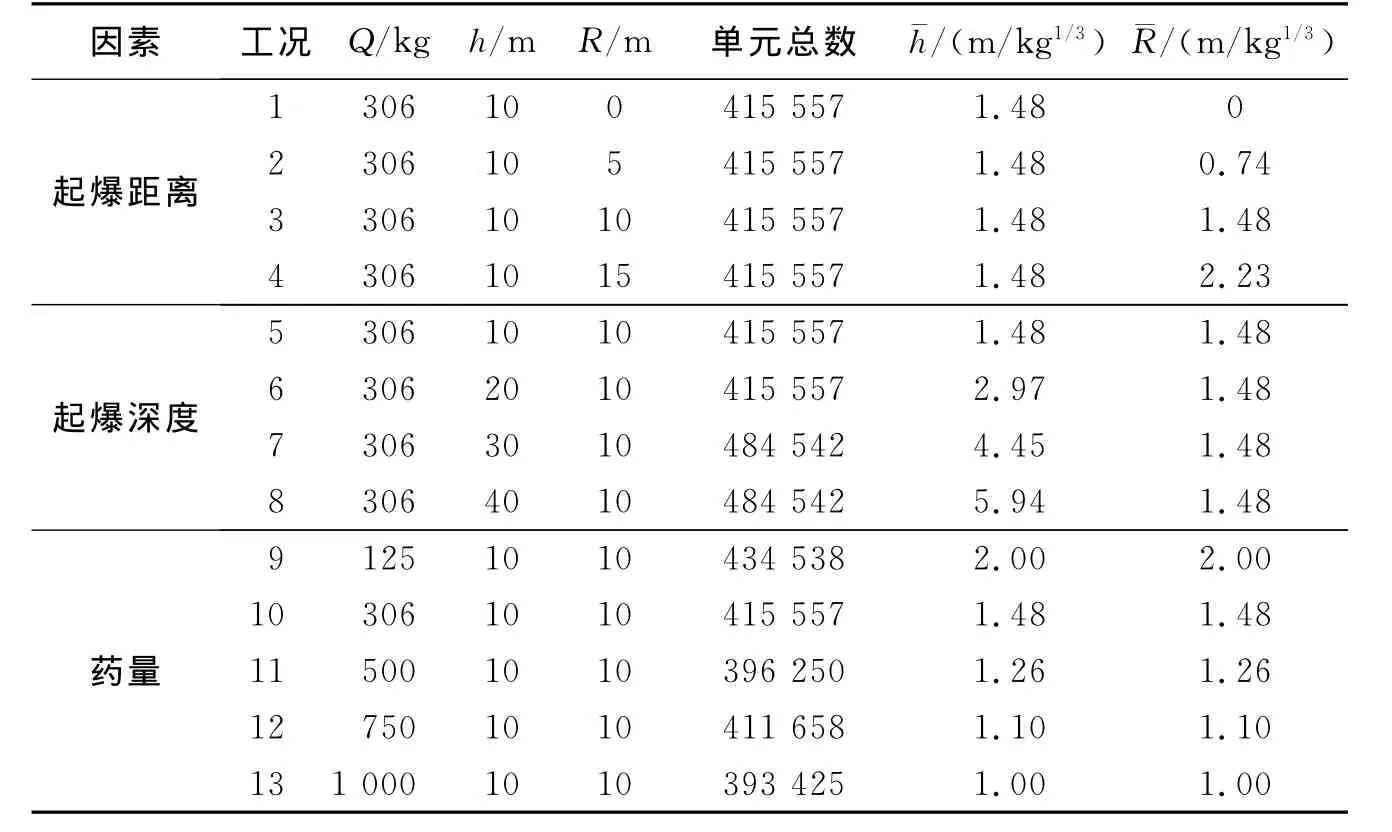
表1 多因素对大坝破坏模式影响的工况设计Table1 Calculation cases on dam of failure mode under multiple factors

2.3 大坝破坏模式对炸弹起爆距离的敏感性分析

图4为制导炸弹（Q＝306kg）起爆深度为10m（比例爆炸深度1.48m／kg1／3）工况下的大坝破坏模式。由图可知，当制导炸弹起爆深度一定时，不同比例爆炸距离工况下，大坝破坏模式及破坏程度相差较大。在工况1（R＝0）中，炸药在大坝上游表面发生爆炸，爆轰压力直接作用于大坝表面，该处混凝土压缩屈服，首先被压碎，形成爆炸压缩漏斗坑；当压缩应力波传播至坝顶时反射形成强拉伸波，使坝顶受拉而发生震塌破坏；同时在坝头与上游面直立面交接处，由于较大拉应力和剪应力，发生冲切破坏，裂缝由此处开展并扩展至下游面，形成贯穿性裂缝破坏。在工况2（R＝5m）中，由于制导炸弹距坝上游面距离较小，坝上游面受到水冲击波荷载较大，上游面局部区域混凝土被压碎脱落，形成爆炸压缩漏斗坑；当压缩应力波传播至坝顶时反射形成强拉伸波，使坝顶受拉破坏而发生震塌破坏；随后在下游折坡处附近，发生冲切破坏，产生贯穿上下游面的裂缝。在工况3（R＝10m）中，坝头和上游直立面距爆源均较近，在爆炸冲击荷载作用下，该截面变化处产生很大的剪应力和拉应力，开裂从此处开始扩展至下游面，形成贯穿性裂缝，为脆性冲切破坏；当压缩应力波传播至坝顶时反射形成强拉伸波，使坝顶局部区域受拉破坏而发生震塌破坏。在工况4（R＝15m）中，水面附近因受水面切断效应，水冲击波超压峰值很弱，仅在坝头与坝上游直立面交接处产生局部开裂破坏，坝体整体稳定性不受影响。

图4 不同爆心距下的大坝破坏模式Fig.4 Dam failure mode under different blast center distances

图5为在水下爆炸冲击荷载作用下坝顶顺水流向位移时程曲线，图6为大坝吸收的内能时程曲线。由图5可知，在水下爆炸冲击荷载作用下，大坝易产生反弹现象，主要由于化爆荷载作用时间相对较短，一般仅数毫秒到几十毫秒，高频丰富，易引起结构产生反弹；随着比例爆炸距离的增大，大坝动力响应逐渐减小，当比例爆炸距离小于1时，大坝动力响应规律及趋势较接近，且水下贴坝面爆炸时，大坝动位移及破坏效应最大，最大位移为7.15cm；当比例爆炸距离为1.48时，大坝动力响应比贴爆面爆炸有很大的降低。由图6可知，随着比例爆炸距离的增大，大坝吸收高能炸药的内能逐渐较小，当水下贴爆面爆炸时，大坝吸收的能量最大，破坏效应最严重。

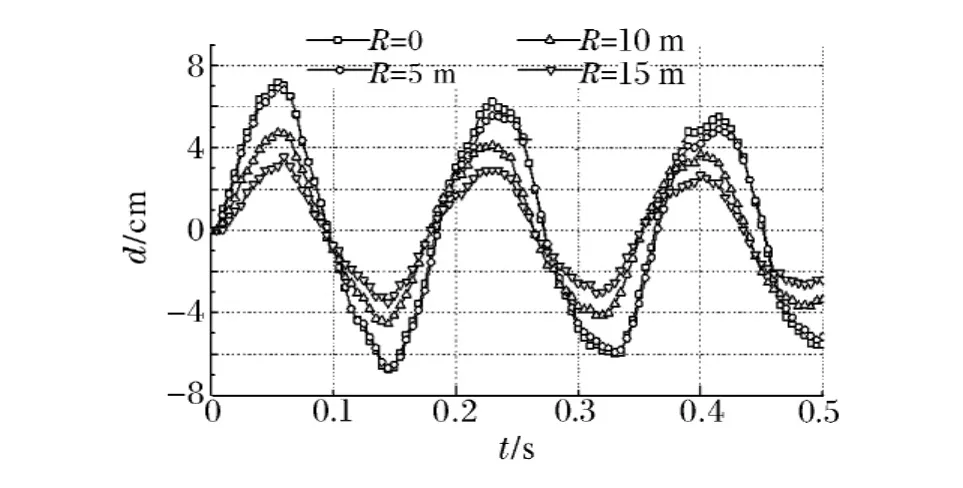
图5 大坝动力时程响应曲线Fig.5 Dynamic time－history response curves

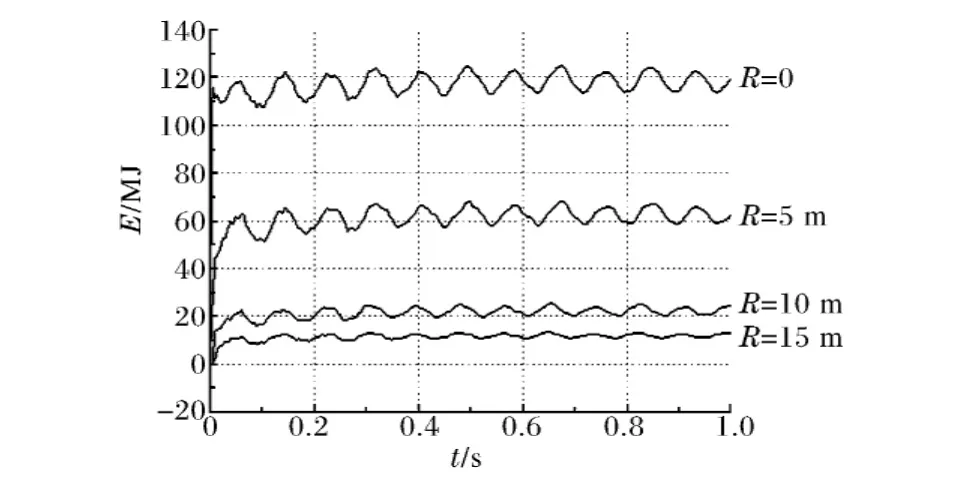
图6 内能变化图Fig.6 Internal energy curves

对比工况1～4可知，当制导炸弹药量和起爆深度一定时，随着比例爆炸距离的增大，大坝受水下爆炸冲击波峰值压力逐渐减小，大坝动力响应减弱，破坏范围变小；大坝破坏主要表现为爆炸成坑破坏、震塌破坏和冲切破坏、贯穿性裂缝破坏。

2.4 大坝破坏模式对炸弹起爆深度的敏感性分析

图7为制导炸弹（Q＝306kg）距坝前距离为10m（比例爆炸距离1.48m／kg1／3）工况下的大坝破坏模式。由图可知，在工况5（h＝10m）中，坝头和上游直立面距爆源均较近，在爆炸冲击荷载作用下，该截面变化处产生很大的剪应力和拉应力，开裂从此处开始扩展至下游面，形成贯穿性裂缝，为脆性冲切破坏；当压缩应力波传播至坝顶时反射形成强拉伸波，使坝顶局部区域受拉破坏而发生震塌破坏。在工况6（h＝20m）中，爆炸冲击波峰值荷载作用在坝上游面，以下游折坡处为支撑，在该高程上游面产生较大拉应力，首先开裂并扩展至下游折坡处，且当冲击波作用在坝头时，在坝头与上游直立面交接处也产生开裂，开裂深度为6.5m左右。在工况7（h＝30m）中，由于与爆源同一高程处坝体较厚，具有较高的抗爆性能，当爆炸冲击波传播到坝头上游面时，同样产生较大的拉应力和剪应力，裂缝初始位于坝头与直立面交接处，开裂深度为5.2m左右；当冲击波传到坝下游折坡处时，压缩应力波与反射波叠加形成强拉伸波，在下游折坡处产生拉应力集中，使坝体开裂，并向坝体内部扩展深度约10.8m。在工况8（h＝40m）中，炸药起爆深度再增大，比例爆炸深度5.94m／kg1／3＞5.00m／kg1／3，属于深水爆炸；水中冲击波的传播受水压影响较大，且与爆源同一高程处的坝体厚度更大，该区域未发生破坏；当压缩波传播至下游面时，由于应力入射波和反射波叠加作用，在坝体下游折坡处产生开裂，并向上游扩展7m左右。

图7 不同起爆深度下的大坝破坏模式图Fig.7 Dam failure mode under different detonation depths

对比工况5～8可知，当制导炸弹的爆距为10m时，在起爆深度为分别10、20m的爆炸冲击荷载作用下，大坝在截面突变处均产生贯穿性裂缝；当炸弹起爆深度为30m时，大坝在下游折坡处及坝头与上游直立面处均产生开裂，但裂缝未贯穿上下游面；炸弹起爆深度为40m时，大坝在下游折坡处产生开裂，并向上游扩展；在比例爆炸距离和炸弹药量一定条件下，随着比例爆炸深度的增大，大坝破坏范围先增大后减小，说明对于挡水坝段，坝颈部位是抗爆薄弱部位。

2.5 大坝破坏模式对炸弹药量的敏感性分析

图8为爆炸起爆水深为10m、爆心距为10m时，不同炸弹用量下大坝的破坏模式。当炸弹起爆深度和爆心距一定时，坝面受到水下爆炸冲击荷载幅值随炸弹药量的增大而增大，不同炸弹药量下的大坝破坏形态分析如表2所示。

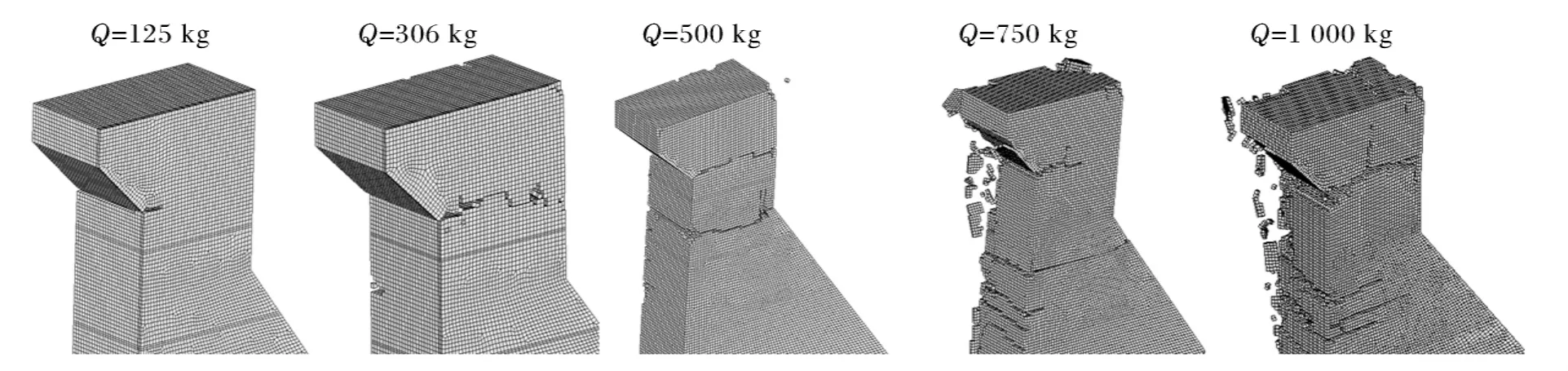
图8 不同炸弹药量下的大坝破坏模式Fig.8 Dam failure mode under different amounts of explosive

表2 不同炸弹药量下的大坝破坏模式分析表Table2 The analysis of dam failure mode under different amounts of explosive

在水下爆炸冲击荷载作用下，混凝土重力坝坝头与上游直立面交接处及下游折坡处附近，受较大剪应力和拉应力作用，易产生贯穿性裂缝破坏。制导炸弹在坝前10m爆炸时，各水深下大坝均发生破坏，且起爆水深为20m时，破坏最严重；当制导炸弹在水下10m起爆时，随着爆心距大的增大，大坝破坏效应逐渐减小，当爆心距为15m时，大坝破坏效应较小。随着炸药当量的增大，大坝受到的爆炸冲击波荷载幅值逐渐增大，坝体上游面受损区域及深度也因此逐渐增大，大坝破坏趋于严重，当炸弹药量进一步增大时，可导致坝体上部块体出现倾倒溃坝的严重破坏模式。

3 结 论

（1）库前水下爆炸冲击荷载作用下的大坝破坏模式不仅与大坝自身的动力特性有关，还与炸弹起爆的水下深度、爆心距及炸弹药量有关。随着比例爆炸深度的增大，大坝破坏范围先增大后减小；随着比例爆炸距离的增大，大坝破坏范围逐渐减小；随着炸弹药量的增大，大坝破坏趋于严重，坝体上游面受损区域及深度也逐渐增大，当炸弹用量进一步增大时，坝体上部块体将产生倾倒溃坝的严重破坏模式。

（2）混凝土重力坝坝头是大坝抗爆性能的薄弱部位，制导炸弹在水下爆炸引起破坏主要表现为压碎破坏、震塌破坏、脆性冲切破坏，主要破坏模式为：坝上游迎爆面混凝土的爆炸成坑破坏、坝顶及坝下游面的震塌破坏、坝头与上游直面交接处及下游折坡附近的脆性冲切破坏，并出现贯穿上下游面的贯穿性裂缝破坏。

［1］高勇军，王伟策，陈小波.浅层水中爆炸冲击波压力的测试与分析［J］.爆破，1999，16（1）：9－13.GAO Yong－jun，WANG Wei－ce，CHEN Xiao－bo.Testing and analysis on shockwave pressure generated by explosion under shallow water［J］.Blasting，1999，16（1）：9－13.

［2］顾文彬，叶序双，张鹏祥.浅层水中爆炸水底影响的试验研究［J］.解放军理工大学学报，2001，2（2）：55－58.GU Wen－bin，YE Xu－shuang，ZHANG Peng－xiang.Experiment studies of bottom influence in shallow layerwater explosion［J］.Journal of PLA University of Science and Techlogy，2001，2（2）：55－58.

［3］徐俊祥，刘西拉.水中爆炸冲击下混凝土坝动力响应的全耦合分析［J］.上海交通大学学报，2008，42（6）：1001－1004.XU Jun－xiang，LIU Xi－la.Full coupled simulation of concrete dams subjected to underwater explosion［J］.Journal of Shanghai Jiaotong University，2008，42（6）：1001－1004.

［4］李本平，王永，卢文波.制导炸弹在坝前水面爆炸破坏效应研究［J］.爆破，2007，24（4）：7－12.LI Ben－ping，WANG Yong，LU Wen－bo.Study on the damage effect for water surface explosion of precision guided bomb［J］.Blasting，2007，24（4）：7－12.

［5］Malvar L J，Ross C A.Review of strain rate effects for concrete in tension［J］.ACI Materials Journal，1999，96（5）：614－616.

［6］Bischoff P H，Perry S H.Compressive behavior of concrete at high strain rate［J］.Materials and Strucutres，1991，24（144）：425－450.

［7］Holomquist T J，Johnson G R，Cook W H.A computational constitutive model for concrete subjective to large strains，high strain rates，and high pressures［C］∥Jackson N，Dickert S.The 14th International Symposium on Ballistics.USA：American Defense Prepareness Association，1993：591－600.

［8］Tai Y S，Tang C C.Numerical simulation：The dynamic behavior of reinforced concrete plates under normal impact［J］.Theoretical and Applied Fracture Mechanics，2006，45（2）：117－127.

［9］王涛，余文力，王少龙，等.国外钻地武器的现状与发展趋势［J］.导弹与航天运载技术，2005（5）：51－56.WANG Tao，YU Wen－li，WANG Shao－long，et al.Present status and tendency of foreign earth－penetrating weapons［J］.Missles and Space Vehicles，2005（5）：51－56.

［10］Livermore Software Technolohy Corporation.LS－DYNA keyword user’manul［Z］.California：Livermore Software Technolohy Corporation，2006.

［11］Weathersbly J H.Investigation of bond slip between concrete and steel reinforcment under dynamic loading conditions［D］.USA：Louisiana State University，2003.