改进的卫星广播星历参数模型及其算法

2012-09-18詹武平诸毓武

上海航天 2012年1期

詹武平,诸毓武

(1.国防科学技术大学电子科学与工程学院,湖南长沙 410073;2.中国人解放军海军驻上海地区航天系统军代室,上海 201109)

0 引言

卫星导航技术在国防和国民经济领域的作用日益突出,是一项高效益的综合性高新技术。除已在轨运行的全球卫星定位系统(GPS)和全球卫星导航系统(GLONASS)外,欧洲正在建设伽利略导航系统,我国也在建设新一代北斗导航系统。导航系统研究包括系统的顶层设计、建设和应用开发等,导航卫星的广播星历参数设计是其中的热点[1-9]。导航卫星广播星历参数模型及其参数内容决定了广播星历的精度,也决定了用户定位算法的复杂程度。星历参数算法的研究一般可分为三种。一是以GPS星历参数模型为基础,研究卫星的开普勒轨道根数及其改正系数的处理算法,利用这些参数可外推卫星的坐标与速度。二是基于GLONASS星历参数模型,处理获得一定时刻的卫星的坐标和速度,根据该时刻的坐标与速度用积分法外推卫星轨道参数。三是采用多项式拟合卫星一段时间内的运行轨道,获得拟合多项式的系数,利用这些系数外推卫星的坐标与速度。设计导航卫星的星历模型及算法时,需综合考虑各种算法的特点,尽可能使用模型参数少、拟合精度高、外推能力强,以及用户算法简单的星历模型。GPS星历参数模型一般包含参数15个。可通过线性化观测方程,用最小二乘法逐步迭代解得星历参数的估值。本文提出了一种基于GPS星历参数模型的改进星历参数模型,给出了星历参数的计算与卫星轨道外推方法。

1 GPS广播星历参数模型

GPS由GPS卫星星座、地面监控系统和GPS信号接收机三部分组成。GPS星座有轨道平面6个,均布卫星24颗,地球上每个用户可同时接收到至少4颗GPS卫星的导航定位信号,测量出用户接收机至导航卫星的距离,利用测距定位原理,能快速处理获得用户接收机的三维坐标,实现全球性全天候的实时导航定位。

GPS卫星不断向用户发送导航定位信号,用户接收机对这些信号进行解码可得GPS导航信息,主要有卫星星历、卫星时钟改正、电离层时延修正、卫星工作状态和C/A码转到捕获P码,其中的卫星钟差修正参数、卫星的轨道根数及其改正数等信息更新率为1 h。GPS卫星采用轨道根数和相应的部分轨道摄动系数作为卫星星历内容,包括开普勒轨道参数6个和轨道摄动参数9个。开普勒轨道参数分别为卫星轨道半长轴a的平方根、卫星轨道偏心率e、参考时刻的轨道倾角i、平近点角M、参考时刻的升交点赤经Ω和近地点角距ω。其中i,Ω确定了卫星轨道面的空间取向;ω确定了卫星椭圆轨道a的方向;确定了卫星椭圆轨道的形状;M确定了某时刻卫星在其轨道上的位置。轨道摄动参数为平近地点角速度改正数Δn、近地点角距摄动量dω/d t、升交点赤经变化率﹒Ω、轨道倾角变化率﹒i、升交角距正余弦调和改正项振幅Cus,Cuc、轨道倾角正余弦调和改正项振幅Cis,Cic、轨道半径正余弦调和改正项振幅Crs,Crc。由这些卫星的轨道参数,可确定卫星在某时刻卫星的坐标与速度,也可外推一定时间段内高精度的卫星轨道位置与速度。

卫星运动的状态参数X和观测方程Y可用这些参数表示为

式中：X0为星历参数,由上述15个参数组成的矢量;t0,t分别为初始时刻和时间。当观测量多于15个时,对式(1)作线性化处理,用最小二乘估计可得X0改正量的最优估值

式中：H为观测量对星历参数的偏导数阵;ΔY为卫星轨道的实际测量值与利用星历参数估计的测量值之差。迭代计算开始时,由初始观测量估计卫星的轨道根数,其余摄动参数取为0,用式(2)逐步改进星历参数,直至获得满意的星历参数结果。

由上可知：GPS星历参数估计算法较复杂,但用户算法简单。GPS星历轨道外推能力强,卫星定位精度较高[1-2]。GLONASS广播星历参数个数较少,但用户算法较复杂,当外推时间较长时,卫星定轨精度降低[7]。考虑卫星服务精度、轨道外推能力与用户算法简单性等因素,研究多集中于基于GPS星历参数模型的算法。

2 改进的星历参数模型

在地球引力作用下卫星的正常轨道为一椭圆,实际卫星运动受地球非球形引力、日月引力、太阳辐射压力、大气阻力以及地球潮汐力等其他天体扰动的影响,卫星的实际运行轨道是一近似椭圆(称为摄动轨道),导致卫星轨道非常复杂。欲精确外推卫星的摄动轨道,须考虑摄动力的影响,星历参数模型的精确性依赖于摄动力的拟合精度。地球非球形引力等主要摄动力与卫星相对地球的位置有关,可认为是升交距角Φ的函数。在GPS星历参数模型中,因地球非球形和日月引力等因素引起的Φ,r,i的摄动量可用2Φ的三角函数拟合[10]。即

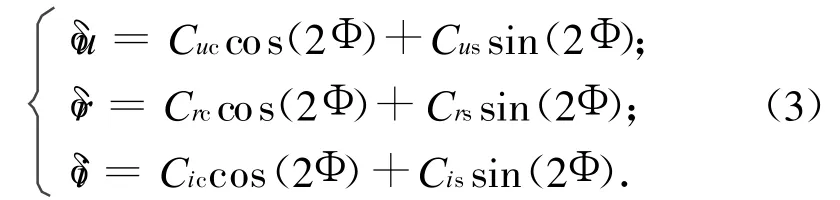
为提高估计精度,式(3)可改写为

式中：cu1～cu4,cr1～cr4,ci1～ci4为系数。可发现式(3)是式(4)的一种特例,显然式(4)能以更高精度拟合卫星轨道的摄动量,从而提高卫星轨道的外推能力。这种改进的摄动量的表达式增加了2个三角函数与6个乘法的计算量,其他轨道根数与轨道摄动系数的计算方法不变,用户算法仍较简单,可满足实时高精度计算的要求。

为便于处理,令

则式(5)可简化为

用最小二乘法估得ΔX,并更新星历参数为

梯度矩阵∂Y(X中的元素是卫星的坐标对星历参数的偏导数,卫星的观测坐标x,y,z对ω的偏导数分别为

其余的卫星位置对卫星星历参数的偏导数见文献[11、12]。

卫星星历参数对初始的星历参数的梯度矩阵∂X/∂¯Xk对角元素均为1,其中部分矩阵元素满足

迭代计算星历参数时,根据精度要求确定一个小量ε作为迭代结束的判断阈值。计算第k次的迭代残差

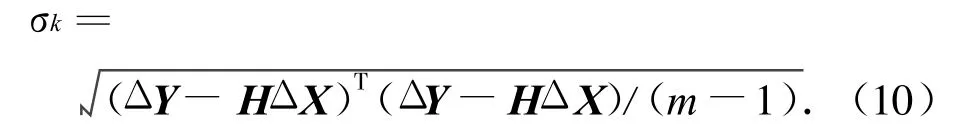
式中：m为观测量个数。当满足

时迭代过程即停。卫星星历参数求解流程如下：

a)由跟踪测量设备确定一段时间内卫星的坐标和速度;

b)由卫星的一组坐标与速度确定卫星的初始开普勒轨道根数;

c)计算观测卫星的坐标对星历参数的偏导数阵;

d)计算开普勒轨道根数以及摄动改正系数的修正量;

e)由修正量改进卫星的开普勒轨道根数及其修正系数;

f)判断迭代停止条件式(11)是否满足,如不满足迭代结束条件则转向步骤c)[8]。

根据迭代计算的卫星星历参数,依次计算卫星的平均角速度、平近点角、偏近点角、真近点角、升交距角,用式(5)计算升交距角摄动量、卫星矢径摄动量、卫星轨道倾角摄动量,由摄动量可计算摄动改正后的升交距角、卫星矢径与轨道倾角,最后获得卫星在地固坐标系中的坐标[10]。

3 算例

设仿真计算的卫星轨道根数为：t0=42 200.0(UTC),a=26 553 409.0 m,e=0.000 824 7,i=17.425°,Ω=54.58°,ω=312.63°,M=325.31°,利用STK软件,考虑70×70阶地球引力场、日月引力、光压和潮汐摄动,计算一段时间内卫星的精密轨道参数序列。用本文的卫星星历参数模型及星历参数计算方法,对1 h的卫星轨道观测坐标进行处理,迭代计算卫星星历参数。再用改进的摄动量计算模型外推5 h的卫星轨道坐标序列。将星历参数外推的坐标序列与卫星的精密轨道坐标作差,可得卫星三维坐标偏差序列Δx,Δy,Δz,结果分别如图1～3所示。

由图1～3可知：用本文的星历参数模型外推的卫星坐标与精密轨道坐标作差较小：轨道外推5 h内,x向坐标之差小于2 m,y向坐标之差小于5 m,z向坐标之差小于1.5 m;轨道外推4 h内,三维坐标误差均小于1 m,外推卫星轨道参数的精度高于文献[1]。表明该星历参数模型较好地拟合了摄动力的影响,外推卫星轨道坐标的能力较强,而计算卫星轨道参数的计算量增加并不明显,可满足实时定位的要求。