在部分信息下股票收益服从隐马尔科夫模型的最优交易策略
2012-09-17费为银石学芹
李 钰,费为银,石学芹,李 娟
(安徽工程大学 数理学院,安徽 芜湖 241000)
在部分信息下股票收益服从隐马尔科夫模型的最优交易策略
李 钰,费为银,石学芹,李 娟
(安徽工程大学 数理学院,安徽 芜湖 241000)
讨论了部分信息下股票支付红利的最优交易策略.考虑一个多种股票模型,股票价格过程满足随机微分方程,股票价格的瞬时收益率由有限状态连续时间的马尔科夫链刻画.在投资者终端财富预期效用最大化目标下,利用隐马尔科夫模型(HMM)滤波理论和Malliavin分析,导出最优交易策略的显式表达式.
投资组合最优化;部分信息;红利率;隐马尔科夫模型(HMM)滤波;Malliavin分析
最优消费投资模型已被众多国内学者所研究,且大多数研究是基于文献[1]的基本假设并加以若干改进.文献[1]解决了理性的家庭投资者对持有的资产如何投资和消费,以实现自己在整个生命周期内累计消费和终端财富的期望效用最大化.但是随着金融市场的不断创新和发展,需要对更加符合实际的模型加以研究并应用于实际.LAKNER[2]提出了在部分信息下最优消费投资选择问题,在证券价格可观测的情况下,即资产价格方程组中的标的布朗运动和漂移过程不能直接被观测时,使用鞅方法推导出了最优消费投资策略.文献[3]推广了上述结论,将漂移过程建模为一个高斯过程,该模型在特殊的情况下就变成了多维的均值回复Ornstein-Uhlenbeck过程.ELLIOTT[4]讨论了有限维滤子问题以及在高斯噪声中观测到的一个连续时间马尔科夫链.SASS等[5]研究一个多种股票市场模型,其中瞬时收益率被建模为一个具有有限状态的连续时间马尔科夫链.依据漂移过程的非标准滤波,使用隐马尔科夫模型(HMM)滤波结论和 Malliavin分析可以导出最优交易策略的显式表达式.这个最优策略可以在数值上被决定,参数可以通过最大期望(EM)算法被估计.HAUSSMANN等[6]将模型推广到随机波动率以及依赖于某些状态变量的更为一般的随机利率.KARATZAS等[7]考虑到股票红利支付,并给出了带股票红利支付的财富动力学.胡慧敏等[8]讨论了部分信息下带有红利的最优投资策略,对Lakner模型进行了推广,并给出了最优投资策略的显式表达式.
众所周知,红利的发放同样也会影响投资者的最优交易策略选择.因此,本文在文献[5]的基础上,对模型作了进一步推广,所得结论更加符合实际.
1 关于股票收益的隐马尔科夫模型
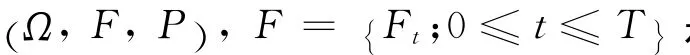
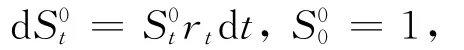


2 最优化和滤波结论
首先引入风险中性测度.易知



3 最优交易策略
本节证明文中主要结论——定理2.该定理给出了最优交易策略的一个显式表达式.在推论中将详细说明幂效用下的最优交易策略.最优策略是由最优折现终端财富的Malliavin导数给定.Malliavin导数的概念及性质,D,D1,1等可参见文献[5].
假设2 设r遵循以下的动力学




便可以得到幂效用下的最优投资策略.证毕.
4 结 语
本文讨论了在部分信息下带有红利的最优消费投资模型,其中股票收益服从HMM.首先定义风险中性测度,其次利用Malliavin分析刻画了在部分信息下的最优投资策略,最后举例说明在幂效用下的最优投资策略.本文在文献[5]的基础上,考虑带有红利收益率的情形,对模型作了进一步推广,使得相关结论更具有实际意义.
参 考 文 献
[1]MERTON R C.Optimum consumption and portfolio rules in a continuous-time model[J].J Economic Theory,1971,3(4):373-413.
[2]LAKNER P.Utility maximization with partial information[J].Stochast Proc Appl,1995,56(2):247-273.
[3]LAKNER P.Optimal trading strategy for an investor:The case of partial information[J].Stochast Proc Appl,1998,76(1):77-97.
[4]ELLIOTT R J.New finite-dimensional filters and smoothers for noisily observed Markov chains[J].IEEE Trans Inf Theory,1993,39(1):265-271.
[5]SASS J,HAUSSMANN U G.Optimizing the terminal wealth under partial information:The drift process as a continuous time Markov chain[J].Finance Stochast,2004,8(4):553-577.
[6]HAUSSMANN U G,SASS J.Optimal terminal wealth under partial information for HMM stock returns[J].Contemp Math,2004,351(2):171-186.
[7]KARATZAS I,SHREVE S E.Methods of mathematical finance[M].New York:Springer,1998.
[8]胡慧敏,费为银,鲍品娟.部分信息情形下带有红利的最优投资模型研究[J].经济数学,2008,25(4):362-366.
Optimal Trading Strategy under Partial Information and HMM for Stock Returns
LIYu,FEIWei-yin,SHIXue-qin,LIJuan
(School of Mathematics and Physics,Anhui Polytechnic University,Wuhu Anhui 241000,China)
An optimal trading strategy is characterized under partial information with the dividend payment.A multi-stock market model is considered where prices satisfy a stochastic differential equation with instantaneous rates of return modeled as a continuous time Markov chain with finitely many states.For the investor's objective of maximizing the expected utility of the terminal wealth,an explicit representation of the optimal trading strategy is derived by using hidden Markov models(HMM)filtering theory and Malliavin calculus.
portfolio optimization;partial information;dividend;hidden Markov models (HMM)filtering;Malliavin calculus
F 224.9
A
1671-0444(2012)06-0758-05
2011-10-28
国家自然科学基金资助项目(71171003);安徽省自然科学基金资助项目(090416225);安徽省高校自然科学基金资助项目(KJ2010A037)
李 钰(1987—),女,安徽芜湖人,硕士,研究方向为金融工程.E-mail:anhuiliyu@yeah.net
费为银(联系人),男,教授,E-mail:wyfei@dhu.edu.cn
