热压自然通风房间的瞬态污染状况分析
2012-09-17杨秀峰亢燕铭
杨秀峰,钟 珂,亢燕铭
(1.东华大学 环境科学与工程学院,上海 201620;2.扬州大学 能源与动力工程学院,江苏 扬州 225127)
热压自然通风房间的瞬态污染状况分析
杨秀峰1,2,钟 珂1,亢燕铭1
(1.东华大学 环境科学与工程学院,上海 201620;2.扬州大学 能源与动力工程学院,江苏 扬州 225127)
热压自然通风向稳态发展的过程中室内空气污染状况必然会不断变化.在热压自然通风瞬态模型的基础上,给出了自然通风的污染物输送模型,理论分析了典型条件下通风房间内污染物浓度的瞬变过程,讨论了主要因素对室内瞬态污染物浓度的影响.研究表明,室内热空气层的污染物浓度和原有冷空气层的污染物浓度均是先升高后降低,且前者的最高值大于后者.增大热源浮升力通量或有效通风面积、减小房间面积或房间高度均可以加速室内污染物浓度的变化,但是增大热源浮升力通量或减小房间面积对污染物浓度的峰值没有影响,而增大有效通风面积或减小房间高度却会使污染物浓度峰值升高.
热压自然通风;瞬态;污染物浓度;峰值
室内热源产生的浮升力驱动的热压自然通风是自然通风的一种重要形式,其基本过程是热源加热周围空气,形成向上浮升的羽流,羽流浮升力产生的烟囱效应使室外空气由下部通风口流入,室内上部的热空气由上部通风口排出,室内逐渐形成垂直温度梯度和空气密度分层[1-4].
在室内外空气污染物浓度不同的条件下,自然通风过程必然会导致室内污染物浓度不断变化.文献[5-7]分析了热压自然通风发展至稳态后室内污染物浓度随时间的衰减规律.其中,文献[5]研究了热源局部分布条件下自然通风气流对室内污染物的冲刷过程,文献[6]则比较了热源均匀分布和局部分布情形下通风气流对室内污染状况的影响,二者均假设室内热空气层和冷空气层的污染物均匀分布.文献[7]根据自然置换通风情形下室内水平截面的运动特性,分别给出了室内热空气层和冷空气层内的污染物输送模型,并与假设污染物充分混合的理论模型进行了比较.然而,对教室和剧院等非长时间使用的公共建筑而言,热压自然通风向稳态发展的过程也很重要,这是因为该过程相对于建筑的使用时间而言并不简短[8-11].因此,了解热压自然通风向稳态发展的过程中室内空气污染状况的瞬态变化,对全面评价热压自然通风对室内环境的影响具有重要的现实意义.
本文旨在分析室内外初始温度相同的条件下,热压自然通风向稳态发展的过程中室内气态污染物浓度的变化规律.在瞬态热压通风理论模型[12]的基础上,给出了一个热压自然通风瞬态发展过程的气态污染物输送模型,并通过数值求解模型控制方程,讨论分析热源浮升力通量、有效通风面积、房间面积和高度等因素对室内瞬态污染物浓度的影响.
1 热压自然通风瞬态发展的理论模型
由于热压自然通风瞬态发展过程的复杂性,关于这方面的理论研究并不多见,其中最具代表性的是文献[8]给出的理论模型.文献[8]研究了室内外初始温度相同、通风口设置在房间顶部和底部、热源位于室内地面的情形下,热压自然通风的瞬态发展过程.其将房间内的气流形式看作置换通风,并假设通风过程中上部热空气层充分混合,温度均匀分布,给出了通风过程中热空气层的体积守恒和浮升力守恒方程.事实上,热空气层内一般存在着温度差异,且位置越高处空气温度越高.文献[8]也指出该模型关于热空气层充分混合的假设可能会低估排出空气的浮升力.
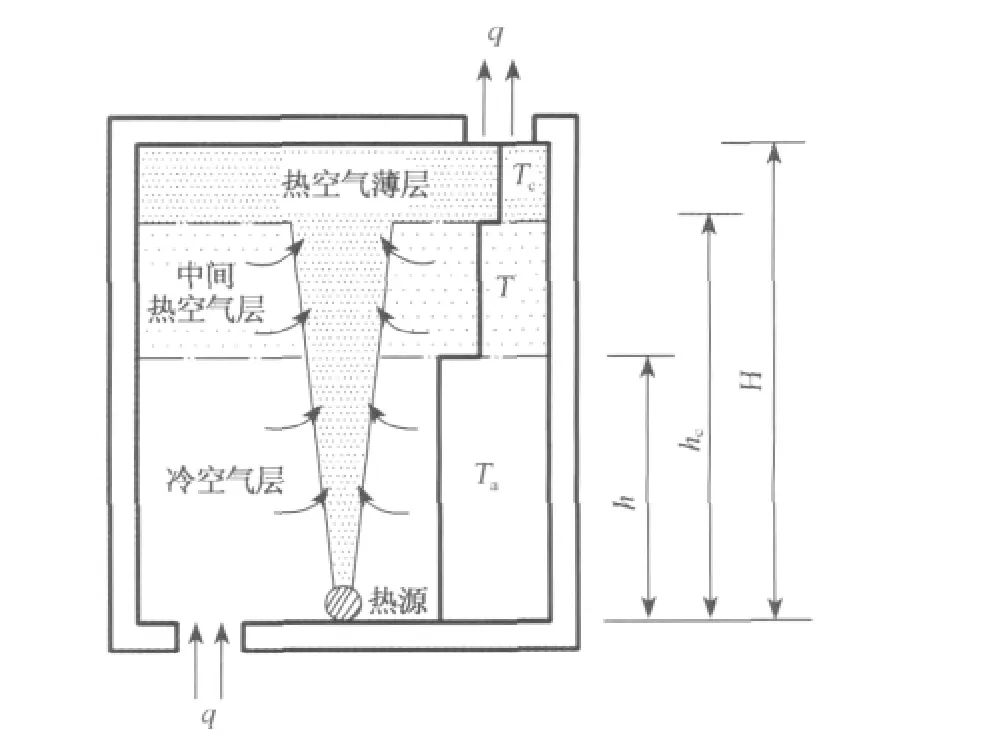
图1 改进模型的空间热分层示意图Fig.1 Schematic diagram of the thermal stratification of the modified model
文献[12]在文献[8]的基础上给出了热压自然通风瞬态发展的改进理论模型.改进模型认为室内热空气层并不是充分混合的,而是由紧靠天花板的热空气薄层及其下方的热空气层两部分组成.于是,通风发展过程中室内空间可以看作由竖向的3个区域组成,即下部的冷空气层、中间的热空气层及天花板处的热空气薄层,如图1所示.图中Ta,T和Tc分别为冷空气层、热空气层和热空气薄层的温度,H,hc和h分别为房间高度和两个热分层界面的高度,q为瞬时通风量.
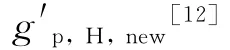
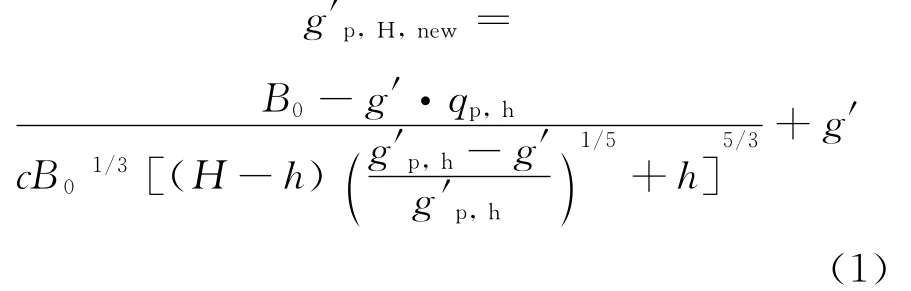
其中:B0为热源的浮升力通量,m4/s3;g′和g′p,h分别为热空气层的浮升力和热分层界面处羽流的浮升力,m/s2;qp,h为热分层界面处的羽流流量,m3/s;c为常数,c= (6α/5)(18απ2/5)1/3(α=0.083,为卷吸系数).
文献[12]认为,羽流穿过冷空气层和热空气层到达天花板后沿天花板水平扩散过程中与周围热空气(浮升力为g′)相混合,因此,可将扩散形成的热空气薄层的浮升力近似看作和g′的算术平均值,即
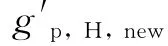
则通风过程中热空气层(包括上部热空气薄层和中部热空气层)的体积守恒方程为

式中:A*为有效通风面积,m2;S为房间面积,m2;t为时间,s.
通风过程中热空气层的浮升力守恒方程为
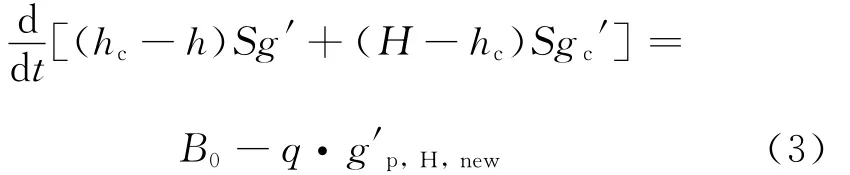
定义下列无量纲参数:

则式(2)和(3)的无量纲形式分别为
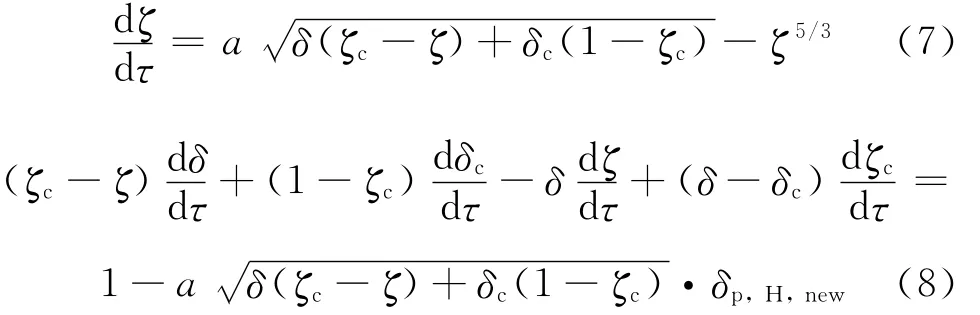
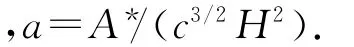
初始条件为τ=0,ζ=1,δ=1.
2 污染物输送模型
通风房间的面积S一般远大于任意高度的羽流截面积,因此,羽流对周围流体的卷吸作用可以近似看作水平的[13].根据体积守恒,任意高度z处羽流外气流垂直方向的平均速度v[7]可以表示为
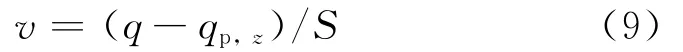
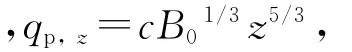
v可能为正、负或0,其值与截面位置和时间有关.文献[12]中将热分层界面到达最低高度ζover和名义稳态高度ζn的时刻定义为通风过程的特征时刻τ2和τ3.在τ=0的初始时刻,地面处的v为0.在0<τ<τ2阶段,地面处对应的v>0,热分层界面高度h处对应的v<0,则热分层界面和地面之间必然存在v=0的截面,将其高度记为h0.在τ2时刻,热分层界面下移至最低位置hover(无量纲高度为ζover),此时q=qp,h,热分层界面处的v=0.在τ2<τ<τ3阶段,q>qp,h,热分层界面处对应的v>0,说明v=0的截面位于热分层界面上方.随着通风过程逐渐趋于稳态,热分层界面和v=0的截面均缓慢向上趋于稳态热分层界面处.热压自然通风发展过程中,空间内典型截面的垂直速度如图2所示.
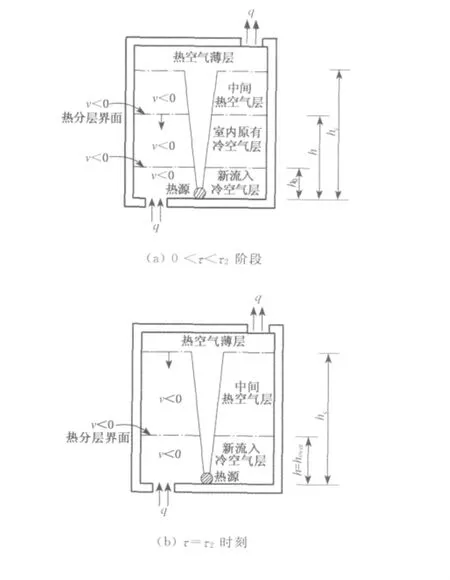
为简化问题,常假设通风口处的气流为单向流,不考虑流入空气与室内空气之间的混合,从而将热压通风房间内的气流形式看作置换通风[1,5,8].于是,通风过程中可以将室内地面附近的新流入冷空气层内的气态污染物看作均匀分布,其浓度与室外空气中的气态污染物浓度ka相等.假设房间上部的热空气层(包括热空气薄层和中间热空气层)和室内原有冷空气层内的气态污染物均匀分布,浓度分别记为ku和k1,则在0<τ≤τ2的通风阶段,室内空间由3个浓度不同的区域组成.当τ>τ2后,室内原有冷空气层消失,室内空间由浓度分别为ku和ka的2个区域组成.当τ=τ3时,通风发展至稳态,通风量和热分界面高度分别取稳态值qss和hss.
2.1 0<τ≤τ2的阶段
该阶段室内热空气层的污染物质量守恒方程为
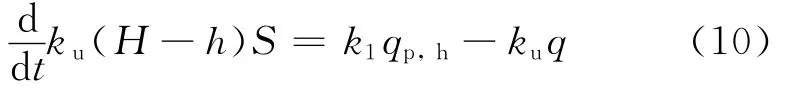
室内原有冷空气层的污染物质量守恒方程为
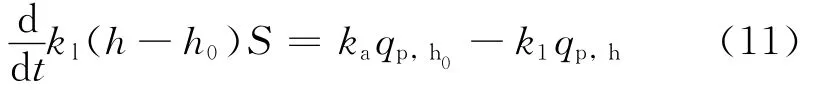
垂直速度v=0的截面距离地面的高度h0可由式(12)得到:
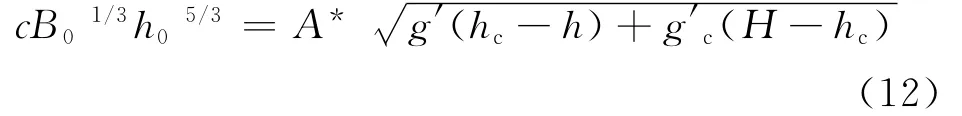
将室内原有的污染物浓度记为k0,并在此基础上定义下列无量纲浓度:
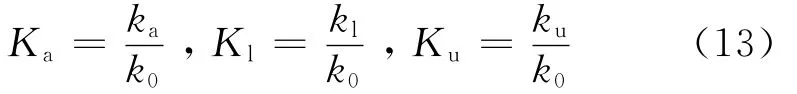
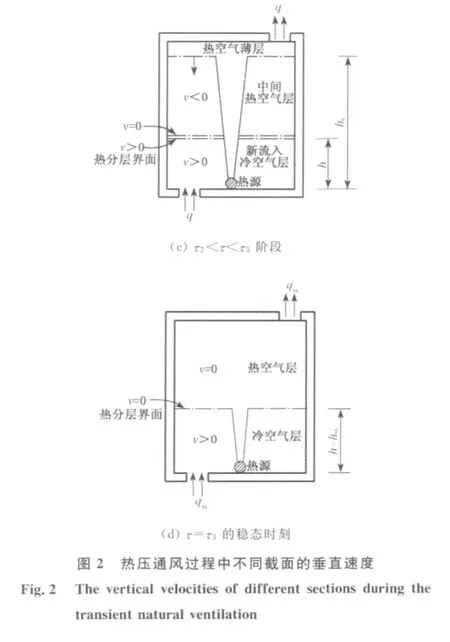
则式(10)和(11)的无量纲形式分别为
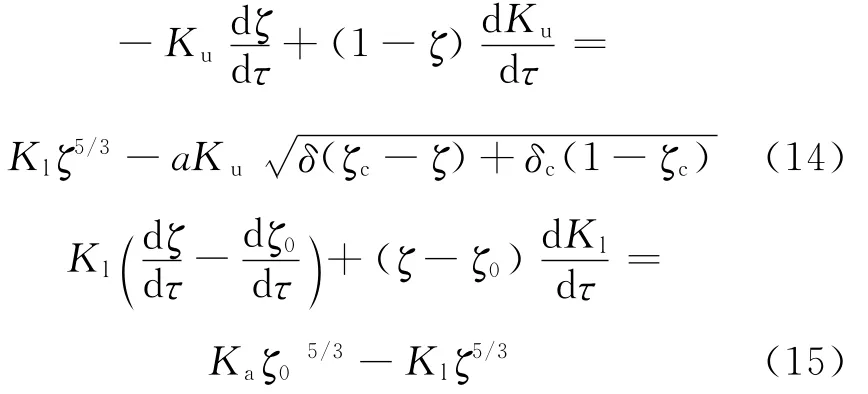
v=0的截面的无量纲高度为
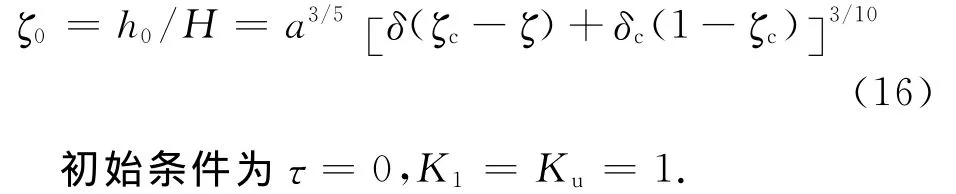
2.2 τ>τ2的阶段
如图2所示,当瞬态通风过程发展至τ2时刻后,室内原有冷空气层消失,热分层界面由最低高度处缓慢上移,界面处的垂直速度v>0,而v=0的截面位于热分层界面上方.v=0的截面将室内空间分为两个浓度不同的区域,截面以上区域的浓度为ku,截面以下区域的浓度为ka.上部区域内污染物质量的守恒方程可以表示为

式(17)的无量纲形式为
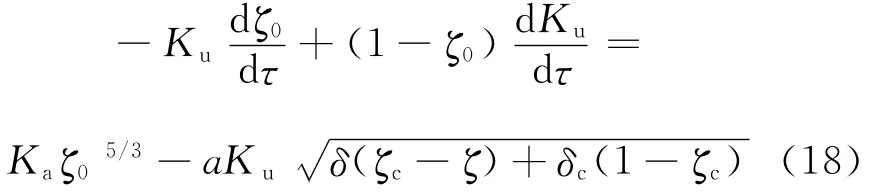
该阶段的起始时刻为τ2,初始条件即为τ=τ2,Ku=Ku,τ2,其中Ku,τ2为τ2时刻室内热空气层的污染物浓度.
3 热压通风房间瞬态污染状况分析
联立热压通风瞬态发展过程的改进模型和上述污染物输送模型,并利用 Mathematica 7.0软件数值求解相关的微分方程组,数值方法为显式RungeKutta法.
图3所示为a=0.2条件下热压通风过程中热分层界面高度ζ、v=0截面的高度ζ0以及原有冷空气层厚度ζ-ζ0的瞬时变化.由图3可知,通风过程开始后热分层界面由天花板处向下移动,v=0的截面由地面处向上移动,两截面在τ2时刻完全重合.这表明通风开始后室内原有的空气层越来越薄,直至消失.τ2时刻以后,两截面均向稳态热分层界面处缓慢移动,且v=0的截面稍高于热分层界面.
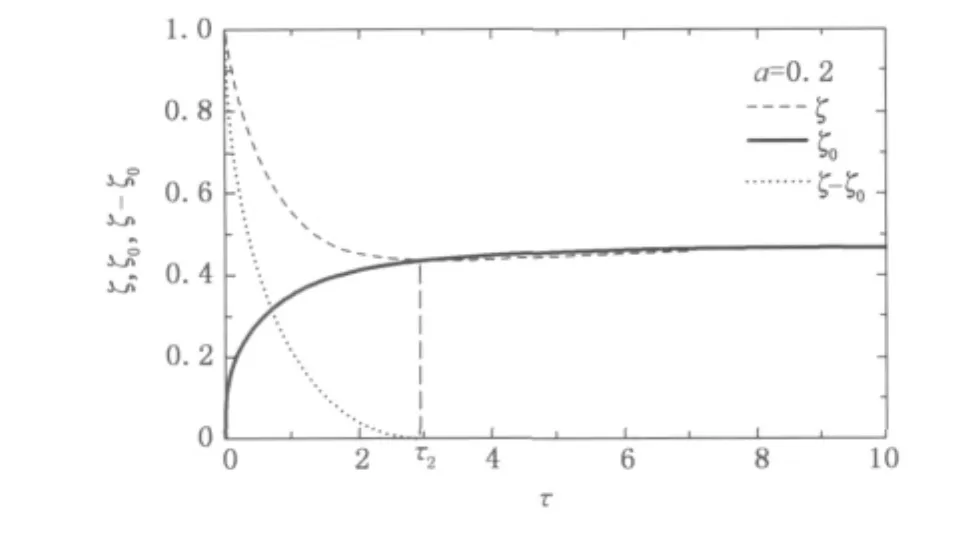
图3 a=0.2条件下ζ,ζ0和ζ-ζ0的瞬时变化Fig.3 Dimensionless heightζ,ζ0andζ-ζ0,as a function ofτfor a=0.2
图4所示为a为0.2、室外污染物浓度Ka=0条件下,热压通风过程中室内污染物浓度的瞬时变化.图4表明,室内热空气层的污染物浓度Ku和室内原有冷空气层的污染物浓度K1均先升高后降低,且K1先于Ku到达最高值,其最高值大于Ku的最高值.对于室内原有冷空气层而言,虽然通风过程中进入该层的羽流中不含污染物(Ka=0),而离开该层的羽流中污染物浓度为K1,使得该层的污染物总量越来越少,但由于通风起始阶段该层的厚度ζ-ζ0迅速减小(见图3),使该层的污染物浓度显著升高.随着通风的不断进行,室内原有热空气层的污染物总量持续减小,该层的厚度变化渐趋平缓,使得该层的污染物浓度K1开始下降.对室内热空气层而言,通风起始阶段进入该层的羽流流量明显大于离开该层的风量,且羽流的污染物浓度(与K1相同)不小于离开该层空气的污染物浓度(与Ku相同),从而使室内热空气层内的污染物总量显著增加,污染物浓度上升.随着通风过程的进行,虽然进入热空气层的羽流流量仍大于通风量,但羽流中的污染物浓度已开始低于排风气流的污染物浓度,从而使热空气层的污染物浓度Ku逐渐降低.当Ku取最大值时,dKudτ=0,则由式(7)和(14)可知Ku=K1,这意味着图4中两曲线的交点即为Ku曲线的最高点.
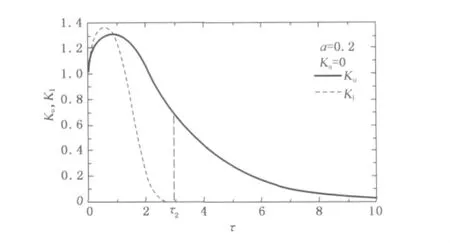
图4 a=0.2、Ka=0条件下室内污染物浓度的瞬时变化Fig.4 Dimensionless pollutant concentration as a function of τfor a= 0.2and Ka=0
图5所示为a为0.2、室外污染物浓度Ka分别为0,0.2和0.5的条件下,热压通风过程中室内无量纲污染物浓度Ku和K1的变化过程.由图5可知,室外污染物浓度Ka不同时,室内瞬时污染物浓度的变化趋势相似,且Ka越大,室内瞬时污染物浓度越大,Ku和K1到达最高值的无量纲时间τ越长.图5还表明,Ka越大,τ2时刻室内原有冷空气层的污染物浓度K1与Ka之间的偏离越大,这说明当室外污染物浓度较大时,即使通风过程进行到室内原有冷空气层即将消失时,该层的污染物浓度也不能降低至室外污染物的浓度水平.
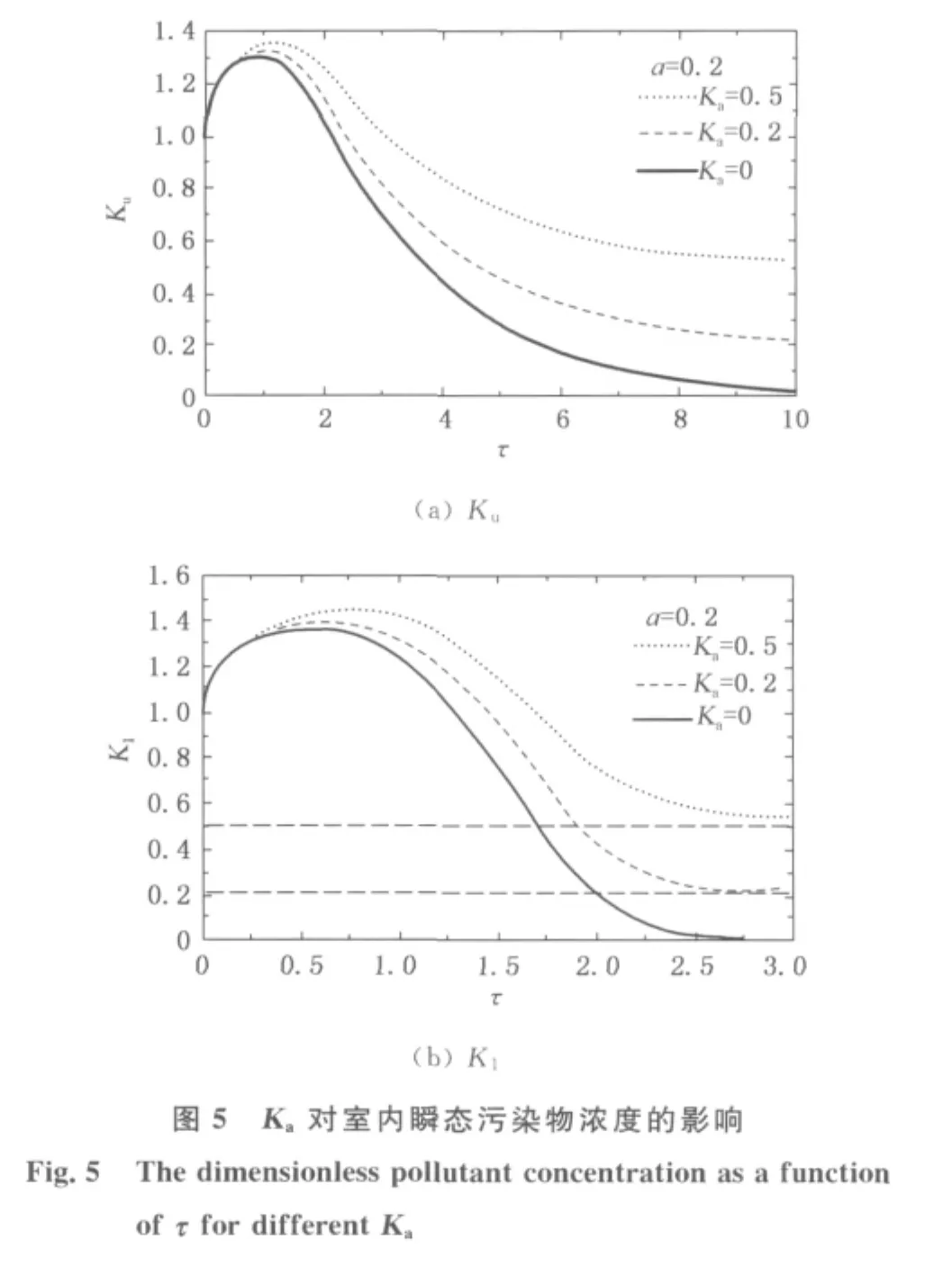
图6所示为室外污染物浓度Ka为0、无量纲有效通风面积a分别为0.2,0.5和1.0条件下热压通风过程中室内无量纲污染物浓度Ku和K1的变化过程.由图6可知,a越大,Ku和K1的最高值越大,且由初始浓度上升到最高值以及由最高值下降到接近室外浓度的过程所需的无量纲时间越短.说明a越大,室内污染物浓度Ku和K1随无量纲时间τ的变化越快.

了解室内污染物浓度随时间t的演变过程更具有实际意义.由上述污染物输送模型可知,室内污染物浓度Ku和K1随无量纲时间τ的变化取决于a和Ka以及瞬态通风参数ζ,ζc,δ和δc.而由瞬态通风过程的理论模型可知,瞬态通风参数仅取决于无量纲有效通风面积a,即在室外污染物浓度Ka一定的条件下,Ku和K1随τ的变化仅与a有关.因此,通风过程中室内污染物浓度Ku和K1随时间t的变化与B0,S,A*和H有关.本文在典型建筑参数[5]的基础上,利用瞬态热压通风的理论模型[12]和污染物输送模型分析B0,S,A*和H对室内瞬态污染状况的影响.为简单起见,以下分析过程中假设Ka=0.
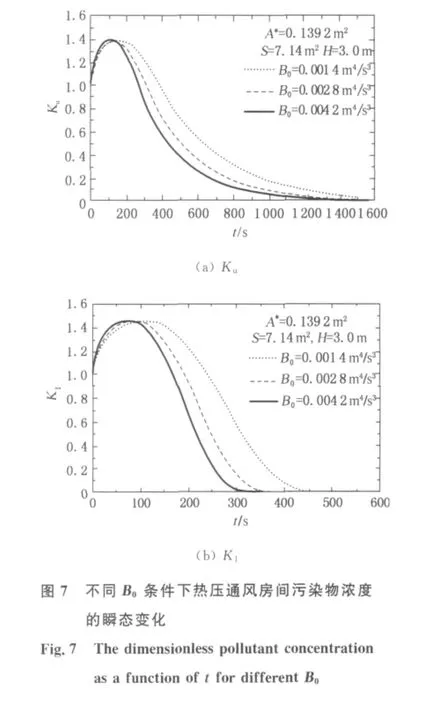
当A*=0.139 2m2,S=7.14m2,H=3.0m,B0=0.001 4,0.002 8,0.004 2m4/s3时,通风过程中室内热空气层的污染物浓度Ku和原有冷空气层的污染物K1随时间t的变化过程如图7所示.图7表明,B0变化对通风过程中Ku和K1的最高值没用影响,但B0越大,Ku和K1由初始浓度上升至最高值的过程和由最高值下降的过程均越短,即室内污染物浓度的变化越迅速.这是因为当B0增大而A*,H和S不变时,无量纲通风面积a不变,则无量纲浓度Ku和K1随无量纲时间τ的变化过程不变.而由式(4)可知,B0越大,某无量纲时刻τ对应的时间t越小,这表明虽然室内污染物浓度变化到某值所需的无量纲时间τ不变,但所需的时间t越短.
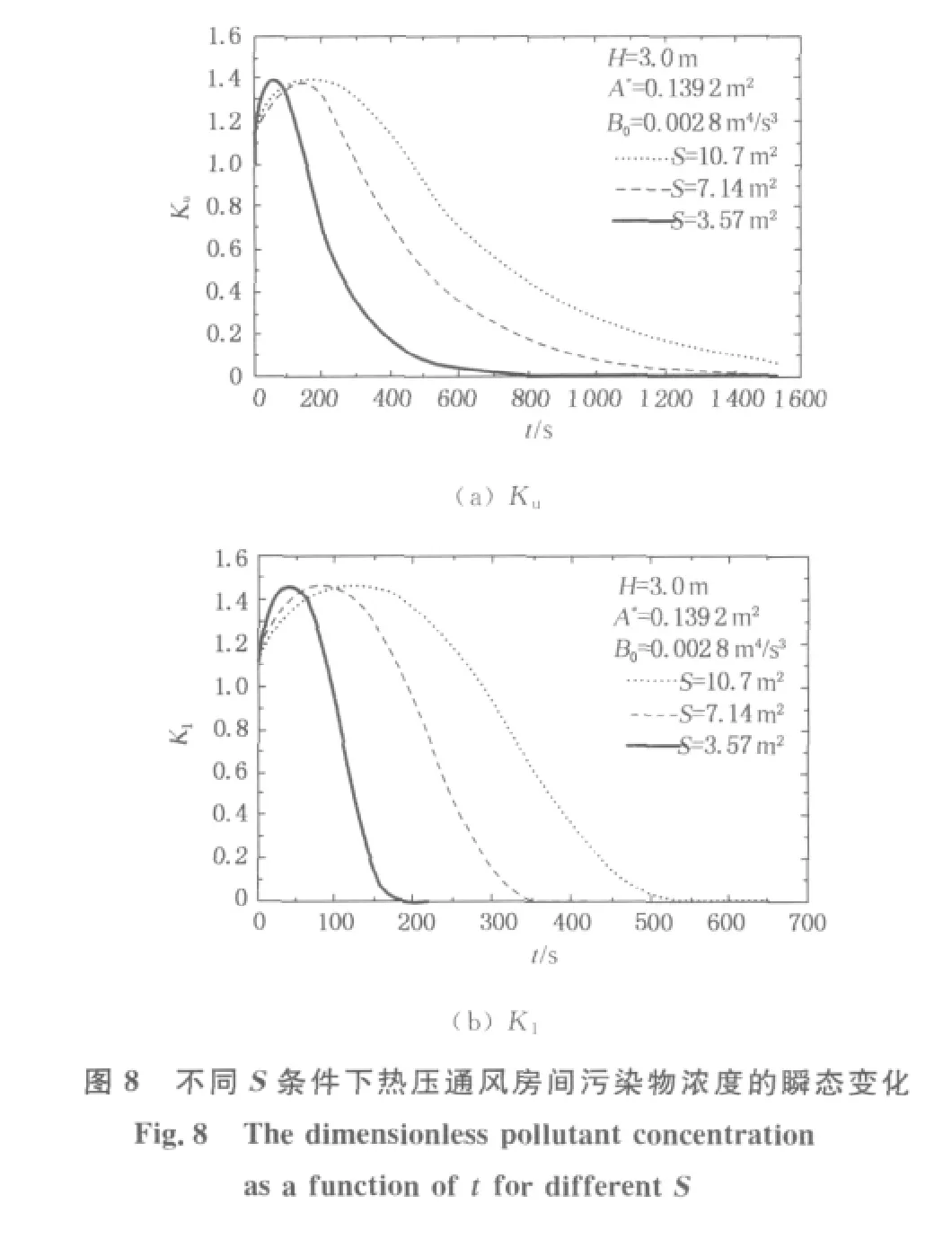
当A*=0.139 2m2,B0=0.002 8m4/s3,H=3.0m,S=3.57,7.14,10.7m2时,热压通风导致的室内污染物浓度Ku和K1随时间t的变化曲线如图8所示.由图8可知,S减小对室内瞬态污染物浓度的影响与B0增大的情形类似,即S越小,室内污染物浓度变化到某一水平所经历的时间t越短,但S变化不会对Ku和K1的峰值产生影响.由热压通风过程的理论模型和污染物输送模型可以得知,当S变小而B0,A*和H不变时,某个无量纲时刻τ对应的热压通风特性参数和无量纲污染物浓度均保持不变,而式(4)表明该无量纲时刻τ对应的时间t减小.因此,S越小,热压通风气流对室内污染物的冲刷过程越迅速有效.
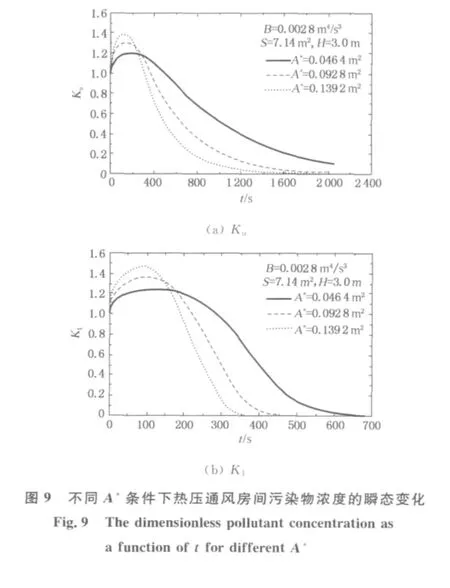
当B0=0.002 8m4/s3,S=7.14m2,H=3m,A*=0.046 4,0.092 8,0.139 2m2时,热 压 通 风 房 间 的瞬态污染物浓度曲线如图9所示.图9表明,A*越大,室内热空气层和原有冷空气层的污染物浓度随时间的变化率越大,Ku和K1的上升阶段和下降阶段均显著缩短,这与图7中B0增大及图8中S减小的情形类似.但当A*增大而其他条件不变时,室内污染物浓度Ku和K1的峰值也相应增大,该现象与图7和8的现象并不相同.
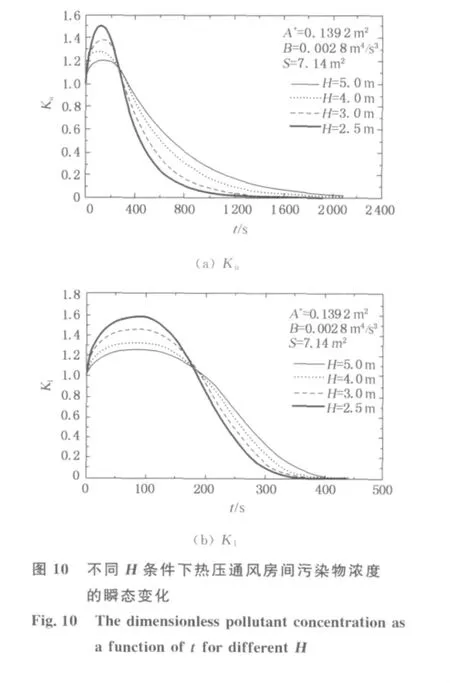
当B0=0.002 8m4/s3,S=7.14m2,A*=0.139 2m2,H=2.5,3.0,4.0,5.0m时,热压通风过程中室内的瞬态污染物浓度如图10所示.由图10可知,当空间高度H减小而其他因素不变时,热压通风可以使室内污染物浓度在相同时间内的变化幅度明显增大.此外,图10还表明,H越小,通风过程中室内污染物浓度的最高值越大,这与图9的现象类似.但不同H对应的Ku和K1变化曲线均分别经过除初始点之外的共同点,该现象与图9明显不同.
4 结 语
本文在热压通风瞬态发展改进模型的基础上,给出了通风房间的污染物输送模型,并通过联立求解两模型的相关方程,讨论分析了典型条件下热压通风发展过程中室内污染物浓度的变化规律.本文的主要结论如下:
(1)通风过程中室内热空气层的污染物浓度Ku和室内原有冷空气层的污染物浓度K1均是先升高后降低,且K1先于Ku到达最高值,其最高值大于Ku的最高值,当Ku取其最高值时,K1与Ku相等;
(2)室外污染物浓度Ka越大,室内瞬时污染物浓度越大,Ku和K1到达最高值的无量纲时间τ越长;
(3)无量纲有效通风面积a越大,Ku和K1的最高值均越大,而Ku和K1的上升过程和下降过程所需的无量纲时间越短;
(4)增大B0、减小S、增大A*或减小H均可以加速热压通风房间内污染物浓度的变化,但是增大B0或减小S对污染物浓度的峰值没有影响,而增大A*或减小H却会使污染物浓度峰值升高.
参 考 文 献
[1]LINDEN P F,LANE-SERFF G F,SMEED D A.Emptying filing boxes:The fluid mechanics of natural ventilation [J].Journal of Fluid Mechanics,1990,212:309-335.
[2]ANDERSEN K T. Theoretical considerations on natural ventilation by thermal buoyancy[J].ASHRAE Transactions,1995,101(2):1103-1117.
[3]LI Y,DELSANTE A,SYMONS J.Simulation tools for analysing natural ventilation of large openings [J].AIRAH Journal,1997,51(11):21-28.
[4]LI Y.Buoyancy-driven natural ventilation in a thermally stratified one-zone building [J].Building and Environment,2000,35(3):207-214.
[5]HUNT G R,KAYE N B.Pollutant flushing with natural displacement ventilation[J].Building and Environment,2006,41(9):1190-1197.
[6]KAYE N B,HUNT G R.Heat source modeling and natural ventilation efficiency[J].Building and Environment,2007,42(4):1624-1631.
[7]BOLSTER D T,LINDEN P F.Contaminants in ventilated filling boxes[J].Journal of Fluid Mechanics,2007,591:97-116.
[8]KAYE N B,HUNT G R.Time-dependent flows in an emptying filling box [J].Journal of Fluid Mechanics,2004,520:135-156.
[9]FITZGERALD S D, WOODS A W. Transient natural ventilation of a room with a distributed heat source[J].Journal of Fluid Mechanics,2007,591:21-42.
[10]BOLSTER D,MAILLARD A,LINDEN P.The response of natural displacement ventilation to time-varying heat sources[J].Energy and Buildings,2008,40(12):2099-2110.
[11]FITZGERALD S D, WOODS A W. Transient natural ventilation of a space with localised heating [J].Building and Environment,2010,45(12):2778-2789.
[12]YANG X F,WANG G X,ZHONG K,et al.Transient pollutant flushing of buoyancy-driven natural ventilation [J].Building Simulation,2012,5(2):147-155.
[13]BAINES W D,TURNER J S.Turbulent buoyant convection from a source in a confined region [J].Journal of Fluid Mechanics,1969,37:51-80.
Analysis on Transient Air Pollution in Buoyancy-Induced Naturally Ventilated Enclosures
YANGXiu-feng1,2,ZHONGKe1,KANGYan-ming1
(1.School of Environmental Science and Engineering,Donghua University,Shanghai 201620,China;2.School of Energy and Power Engineering,Yangzhou University,Yangzhou Jiangsu 225127,China)
Indoor air pollution is influenced continuously by the airflow during the development of thermal natural ventilation to its steady state.The theoretical model of pollutant transport during natural ventilation is presented on the basic of the transient model of thermal natural ventilation to analyze the time evolution of indoor pollutant concentration and to explore the effects of main factors on the transient pollutant concentration during ventilation.The results indicate that the pollutant concentrations of the warm air layer and the original air layer both increase earlier and drop later.The maximal concentration of the warm air layer is shown to be greater than that of the original air layer.The variation of indoor pollutant concentration with time can be accelerated by increasing the source buoyancy flux or effective vent area,or decreasing the enclosure floor area or enclosure height.The increase of the source buoyancy flux or the decrease of the enclosure floor area would not affect the peak value of the transient pollutant concentration,which may be elevated by increasing of effective vent area or decreasing of the enclosure height.
thermal natural ventilation;transient;pollutant concentration;peak value
TU 834.1
A
1671-0444(2012)06-0750-08
2012-06-01
江苏省高校自然科学基金资助项目(09KJB560004);国家自然科学基金资助项目(51278094)
杨秀峰(1976—),男,江苏泰兴人,讲师,博士研究生,研究方向为室内空气品质.E-mail:xfyang@yzu.edu.cn
钟 珂(联系人),女,教授,E-mail:zhongkeyx@dhu.edu.cn
