带常利率相依风险模型的有限时破产概率
2012-09-17王开永林金官
王开永 林金官
(1东南大学数学系,南京 210096)
(2苏州科技学院数理学院,苏州 215009)
带常利率相依风险模型的有限时破产概率
王开永1,2林金官1
(1东南大学数学系,南京 210096)
(2苏州科技学院数理学院,苏州 215009)
为了得到带常利率相依风险模型的风险度量,用概率极限理论及随机过程的方法得到了上述模型有限时破产概率的渐近估计.采用有限时破产概率的加权表达式、加权和的一致渐近性质及相依结构的处理方法研究了索赔额之间的相依性、索赔来到时间间隔的相依性及索赔额的分布对带常利率风险模型的有限时破产概率的影响.结果表明:对于索赔额的分布属于控制变化尾分布族、索赔额之间具有类似渐近独立的相依结构及索赔来到时间间隔具有宽相依结构时,带常利率的风险模型的有限时破产概率呈现出一定的渐近性质,此渐近性质与索赔额的分布、常利率、初始资本及时间范围有关.当考虑的时间范围及索赔量变大时,将增加有限时破产概率的上下界;当常利率及初始资本变大时,将减小有限时破产概率的上下界.但索赔额及索赔来到时间间隔的相依性对有限时破产概率的影响不大.
相依风险模型;有限时破产概率;控制变化尾;渐近性
在风险理论的研究中,人们建立了各种不同的风险模型来刻画各种保险业务,本文将重点考虑带常利率的风险模型.早期的研究大都考虑独立的风险模型,但随着研究的深入及实际问题的出现,人们逐渐开始研究相依的风险模型,本文则考虑一类比较宽泛的相依结构.在上述模型下,本文将给出有限时破产概率的渐近估计.
1 相依重尾风险模型
1.1 带常利率风险模型
本文将考虑一带常利率的风险模型.在此模型中,索赔额Xk,k≥1为一列同分布的随机变量,它们具有共同的分布F及某一相依结构.索赔来到的时间间隔θk,k≥1为另一列同分布的随机变量,它们具有另一相依结构且θ1非退化于0点.索赔陆续来到的时刻构成一个准更新记数过程,其中,1A为事件A的示性函数.记更新函数为λ(t)=EN(t),t≥0,且假设对任意0<t<∞,λ(t)<∞.设Λ={t:λ(t)>0}.
到时刻t≥0为止总保费记为C(t),其为一个非负不降的随机过程,其中约定C(0)=0且对任意0≤t<∞,C(t)<∞几乎处处成立(a.s.).假设{Xk,k≥1},{θk,k≥1}及{C(t),t≥0}是彼此独立的.设0≤δ<∞为一个常利率,即时间t以后资本y会变为yeδt.设0≤x<∞为一保险公司的初始资本.从而,到时刻0≤t<∞为止总的储备记为Uδ(x,t),满足

式中为到时刻0≤t<∞为止的总索赔量,当N(t)=0时约定S(t)=0.因此,对任给定的T≥0,在时间段[0,T]内的有限时破产概率定义为[1]

本文将在索赔额Xk,k≥1和索赔来到的时间间隔θk,k≥1分别具有某一相依结构且索赔额分布F属于控制变化尾时,讨论有限时破产概率ψ(x,T)的渐近性.为此,下面将介绍一些随机变量的相依结构及一些常见重尾分布族,然后给出本文主要结果.
1.2 随机变量的相依结构
Wang 等[2]在讨论 ψ(x,T)的渐近性时,介绍了一类比较宽泛的随机变量的相依结构.
定义1 对于随机变量{ξn,n≥1},若存在一有限实数列{gU(n),n≥1}使得对每一个n≥1及所有xi∈(- ∞ ,∞),1≤i≤n,有

则称随机变量{ξn,n≥1}为宽上象限相依(WUOD);若存在一有限实数列{gL(n),n≥1}使得对每个n≥1 及所有xi∈(- ∞,∞),1≤i≤n,有

则称随机变量{ξn,n≥1}为宽下象限相依(WLOD);进而,若{ξn,n≥1}既为 WUOD 又为WLOD,则称随机变量{ξn,n≥1}为宽象限相依(WOD).
在式(2)、(3)中,若gU(n)=gL(n)≡1,n≥2,则分别称随机变量{ξn,n≥1}为负上象限相依(NUOD)及负下象限相依(NLOD);若随机变量{ξn,n≥1}既为 NUOD 又为 NLOD,则称随机变量{ξn,n≥1}为负象限相依(NOD)[3-4].若对所有正整数i≠j,随机变量 ξi与 ξj为 NOD,则称随机变量{ξn,n≥1}为两两负象限相依(NQD)或两两NOD[5].
由WUOD及WLOD的定义,文献[2]给出了关于WUOD及WLOD随机变量的一些性质.
命题11)设随机变量{ξn,n≥1}为 WLOD(或 WUOD),若{fn(·),n≥1}为非降函数,则{fn(ξn),n≥1}仍为 WLOD(或 WUOD);若{fn(·),n≥1}为非增函数,则{fn(ξn),n≥1}为WUOD(或 WLOD).
2)若{ξn,n≥1}为非负 WUOD 随机变量,则对每一个n≥1,

本文将考虑索赔额满足如下相依结构,它是由Geluk 和 Tang[6]引入的.
假设1 对于随机变量{ξn,n≥1},对所有1≤i≠j<∞,
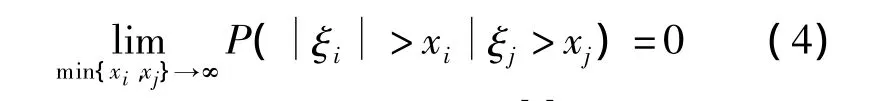
此概念与 Maulik和 Resnick[7]所提出的渐近独立有关.由定义可发现,非负WUOD随机变量及两两NOD随机变量都满足假设1.
1.3 常见重尾分布族
本文将考虑索赔额分布为重尾分布的情形.为此,本节将介绍一些常见的重尾分布族.



1.4 主要结果
在上述带利率的风险模型中,当索赔额Xk,k≥1及索赔来到时间间隔θk,k≥1分别为独立同分布的随机变量时,此带利率风险模型已经得到了广泛研究[1,12-13].
当索赔额Xk,k≥1及索赔来到时间间隔θk,k≥1分别具有某种相依结构时,对有限时破产概率ψ(x,T)也有一些相关研究.Li等[14]考虑了索赔额Xk,k≥1为两两NOD随机变量,其共同的分布,索赔来到时间间隔 θk,k≥1为NLOD且过程{C(t),t≥0}为一线性过程的情形.
对于一般的随机过程{C(t),t≥0}及{N(t),t≥0}是一延迟更新计数过程时,Yang和 Wang[15]的Theorem 2.1也得到了上述结果.
Kong 和 Zong[16]则考虑了索赔额Xk,k≥1 为NOD随机变量,其共同的分布,索赔来到时间间隔θk,k≥1为独立同分布的随机变量且具有共同指数分布的情形.
文献[2]则考虑了索赔额Xk,k≥1为 WUOD随机变量,其共同的分布,且索赔来到时间间隔θk,k≥1为WLOD随机变量的情形,得到了有限时破产概率ψ(x,T)的一致渐近性.
本文将考虑如下2个方面的问题:
1)由于假设1包含了非负WUOD随机变量及两两NOD随机变量,本文将对索赔额Xk,k≥1满足假设1的情形讨论有限时破产概率ψ(x,T)的渐近性.
2)文献[2]讨论了索赔额分布有限时破产概率ψ(x,T)的渐近性.但
的 真 子 集 (见 Embrechts 等[17]的 Example 1.4.2).本文则考虑的情形.
对上述2个问题,本文所得主要结果如下.
定理1 在上述风险模型中,设索赔额Xk,k≥1为满足假设1的随机变量,其共同的分布F∈且,索赔来到时间间隔θk,k≥1为WLOD随机变量且满足对任意ε>0,
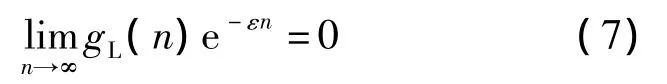

注1 1)定理1将文献[2]中的Theorem 1.1的索赔额Xk,k≥1的相依结构推广到了满足假设1的情形.同时将索赔额分布F的范围由
又设对某个0<T0<∞有p0=P(Y1≤T0)>0,则对任T≥T0,族推广到了族,但仅得到了有限时破产概率ψ(x,T)的弱渐近等价表达式.
2)定理1推广了文献[14]的Theorem 1中F∈的情形的结果.
2 定理1的证明
首先给出一些引理.对任n(n≥1)个实数.对于下面的引理,文献[2]的Lemma 2.3讨论了WUOD随机变量且分布属于∩的情形.
引理1 设n为一正整数,ξk,1≤k≤n为非负随机变量,满足对任 1≤i≠j≤n,式(4)成立.a,b为任给定的正常数且a≤b,则
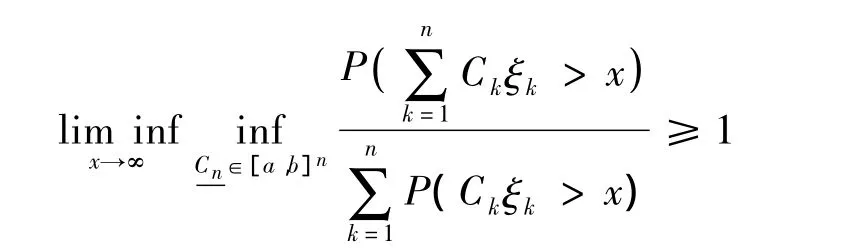
又若ξk,1≤k≤n为同分布的随机变量,其共同的分布,则

证明 由式(4)知,对任 ε>0,存在y0>0使得对任 1≤i≠j≤n,当xi>y0且xj>y0时,
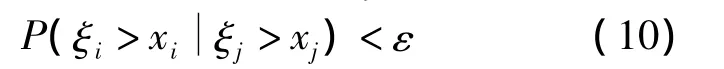
从而由式(10)知,对任1≤i≠j≤n,当x/b>y0时,对一致有

从而由Bonferroni不等式知

另一方面,取一正数L使得L/((n-1)b)>y0.从而对任x>0,


从而,由式(11)~(13)知式(9)成立.
由引理1可得下面的引理.对于此引理,文献[1]的Lemma 3.6讨论了索赔额为独立的情形;文献[15]的 Lemma 3.5则讨论了索赔额为两两NOD的情形.下面的引理讨论了索赔额满足假设1的情形.
引理2 在上述风险模型中,若索赔额Xk,k≥1为满足假设1的随机变量,其共同的分布F∈.Z为任一非负随机变量且与所有随机变量独立,则对任0<T<∞及任给定k≥1,

而由文献[15]的式(3.15)~(3.17)知对任1≤j≤k及充分大x,有

从而由式(15)可知式(14)成立.
下面证明定理1.
证明 将采用文献[1]的方法证明ψ(x,T)的下界.由条件知对任从而,由式(1)、引理2 及Fubini定理知,对任待定的正整数m0,当x充分大时,

而由Markov不等式及命题1知,对任x>0,
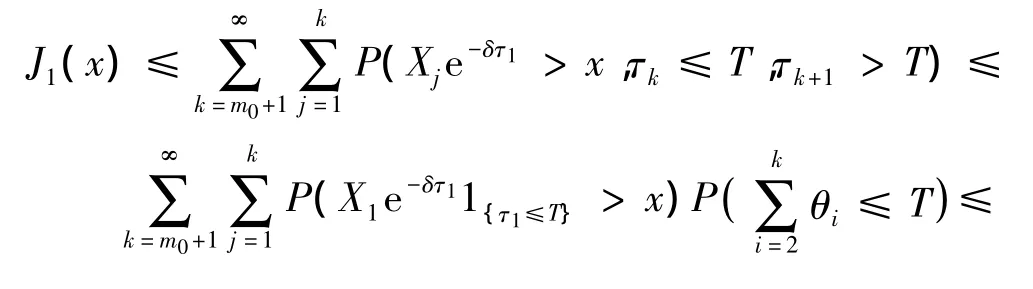

由于 θ1非退化于 0 点,则 0 <Ee-θ1<1.从而由式(7)知,对任 ε >0,存在m0>0,使得

所以,对任x>0及上述m0,
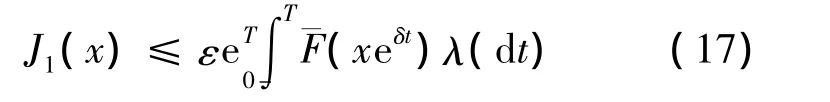
从而,由式(16)、(17)及ε的任意性知

下面证明ψ(x,T)的上界.对任待定的正整数n0,任0<θ<1/2及x>0,
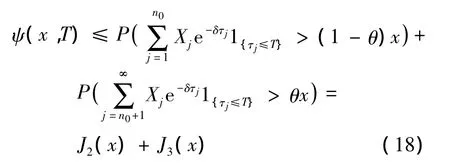
先估计J3(x).将采用Chen 和Ng[18]的方法证明.对任正整数n,使得,有
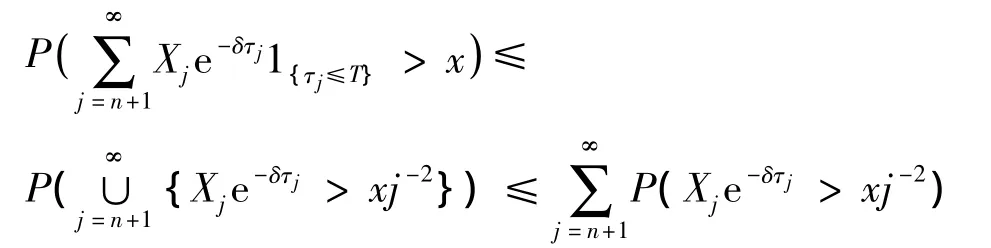

类似地,当x>D1时,
从而,由式(7)知

从而,由式(19)~(21)知
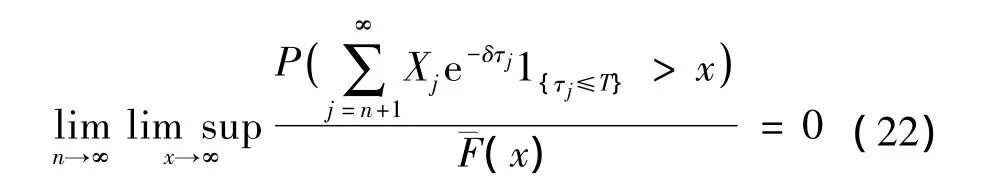
由于p0=P(Y1≤T0)>0,从而对任T≥T0,
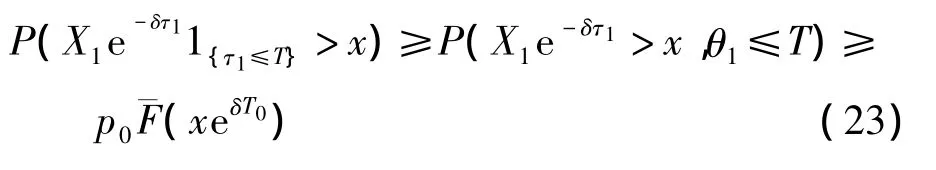
从而对任 ε >0,由式(22)、(23)及F∈知,存在n0>0,对充分大x有

所以,在式(18)中取式(24)中的n0,当x充分大时,
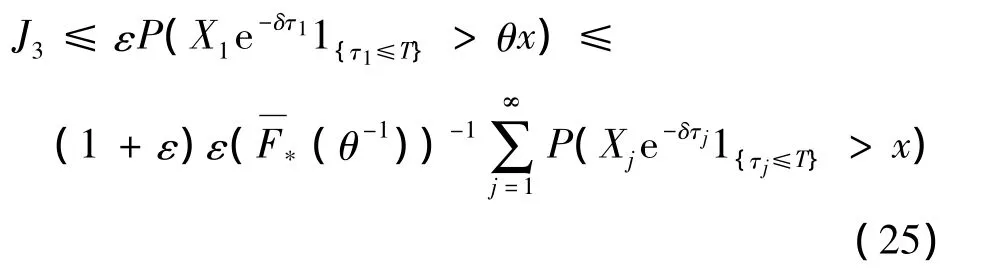
对于J2(x),由引理1知,当x充分大时
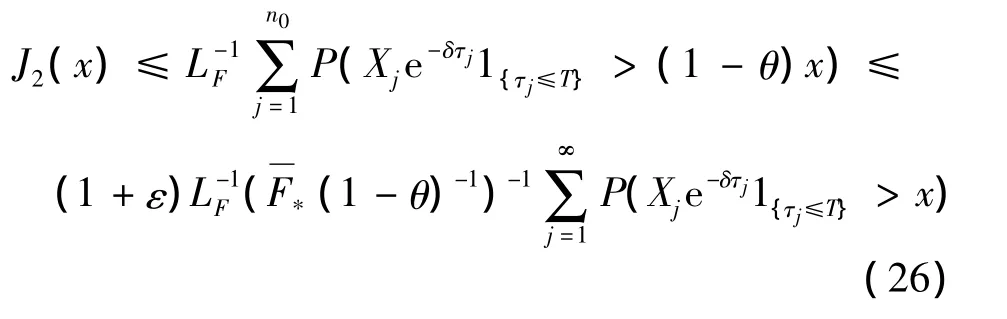
所以,由式(18)、(25)、(26)及 ε 的任意性知

[1]Wang D.Finite-time ruin probability with heavy-tailed claims and constant interest rate[J].Stochastic Models,2008,24(2):41-57.
[2] Wang K,Wang Y,Gao Q.Uniform asymptotics for the finite-time ruin probability of a dependent risk model with a constant interest rate[J/OL].Methodology and Computing in Applied Probability,2011.http://www.springerlink.com/content/q62g3v36033270n8/.
[3] Ebrahimi N,Ghosh M.Multivariate negative dependence[J].Communications in Statistics,1981,10(2):307-337.
[4]Block H W,Savits T H,Shaked M.Some concepts of negative dependence[J].Annals of Probability,1982,10(3):765-772.
[5] Lehmann E L.Some concepts of dependence[J].Annals of Mathematical Statistics,1966,37(2):1137-1153.
[6] Geluk J,Tang Q.Asymptotic tail probabilities of sums of dependent subexponential random variables[J].J Theor Probab,2009,22(4):871-882.
[7] Maulik K,Resnick S.Characterizations and examples of hidden regular variation[J].Extremes,2004,7(2):31-67.
[8]Bingham N H,Goldie C M,Teugels J L.Regular variation[M].Cambridge:Cambridge University Press,1987:135-142.
[9] Cline D B H,Samorodnitsky G.Subexponentiality of the product of independent random variables[J].Stochastic Process and Their Applications,1994,49(2):75-98.
[10]Wang Y,Wang K,Cheng D.Precise large deviations for sums of negatively associated random variables with common dominatedly varing tails[J].Acta Mathematica Sinica:English Series,2006,22(2):1725-1734.
[11]Tang Q,Tsitsiashvili G.Precise estimates for the ruin probability in finite horizon in a discrete-time model with heavy-tailed insurance and financial risks[J].Stochastic Process and Their Applications,2003,108(3):299-325.
[12]Kl¨uppelberg C,Stadtim¨uller U.Ruin probabilities in the presence of heavy-tails and interest rates[J].Scandinavian Actuarial Journal,1998,1998(1):49-58.
[13]Kalashnikov V,Konstantinides D.Ruin under interest force and subexponential claims:a simple treatment[J].Insurance:Mathematics and Economics,2000,27(3):145-149.
[14]Li J,Wang K,Wang Y.Finite-time ruin probability with NQD dominated varying-tailed claims and NLOD inter-arrival times[J].Journal of System Science and Complexity,2009,22(3):407-414.
[15]Yang Y,Wang Y.Asymptotics for ruin probability of some negatively dependent risk models with a constant interest rate and dominatedly-varying-tailed claims[J].Statistics and Probability Letters,2010,80(3/4):143-154.
[16] Kong F,Zong G.The finite-time ruin probability for ND claims with constant interest force[J].Statistics and Probability Letters,2008,78(4):3103-3109.
[17]Embrechts P,Kl¨uppelberg C,Mikosch T.Modelling extremal events for insurance and finance[M].Berlin:Springer,1997:41-42.
[18]Chen Y,Ng K W.The ruin probability of the renewal model with constant interest force and negatively dependent heavy-tailed claims[J].Insurance:Mathematics and Economics,2007,40(4):415-423.
Finite-time ruin probability of dependent risk model with constant interest rate
Wang Kaiyong1,2Lin Jinguan1
(1Department of Mathematics,Southeast University,Nanjing 210096,China)
(2School of Mathematics and Physics,Suzhou University of Science and Technology,Suzhou 215009,China)
In order to obtain the risk measure of a dependent risk model with a constant interest rate,the asymptotic estimates of the finite-time ruin probability are obtained for the above model by using the probability limiting theory and stochastic process.Applying the weighted formula of the finite-time ruin probability,the uniform asymptotics of the weight sums and the way dealing with the dependence structures,the effects of the dependence of the claim sizes,the dependence of the inter-arrival times and the distribution of the claim sizes on the finite-time ruin probability of the risk model with a constant interest rate are investigated.The obtained results show that when the claim sizes have a dominated varying-tailed distribution and a dependence structure similar to the asymptotic independence and the inter-arrival times have a wide dependence structure,the finite-time ruin probability of the risk model with a constant interest rate has some asymptotic properties.These asymptotics have relations with the distribution of the claim sizes,the constant interest rate,the initial capital,and the time range.With the increase in the time range and the claim sizes,the upper and lower bounds of the finite-time ruin probability will increase;with the increase in the constant interest rate and the initial capital,the upper and lower bounds of the finite-time ruin probability will decrease.However,the dependence structures of the claim sizes and the inter-arrival times have little effect on the finite-time ruin probability.
dependent risk model;finite-time ruin probability;dominated varying tail;asymptotics
O211.4
A
1001-0505(2012)06-1243-06
10.3969/j.issn.1001 -0505.2012.06.040
2012-06-20.
王开永(1979—),男,博士,讲师;林金官(联系人),男,博士,教授,博士生导师,jglin@seu.edu.cn.
国家自然科学基金资助项目(11071182,11171065)、国家自然科学基金数学天元基金资助项目(11226211)、江苏省自然科学基金资助项目(BK2012165,BK2011058)、中国博士后科学基金资助项目(2012M520963)、苏州科技学院院科研基金资助项目.
王开永,林金官.带常利率相依风险模型的有限时破产概率[J].东南大学学报:自然科学版,2012,42(6):1243-1248.[doi:10.3969/j.issn.1001 -0505.2012.06.040]
