音频压缩中3种整数型MDCT变换的比较

王 膂 伍家松 Senhadji Lotfi 舒华忠

(1东南大学影像科学与技术实验室，南京 210096)

(2雷恩第一大学信号与图像处理实验室，法国雷恩 35042)

(3东南大学中法生物医学信息研究中心，南京 210096)

音频压缩中3种整数型MDCT变换的比较

王 膂1，3伍家松1，2，3Senhadji Lotfi2，3舒华忠1，3

(1东南大学影像科学与技术实验室，南京 210096)

(2雷恩第一大学信号与图像处理实验室，法国雷恩 35042)

(3东南大学中法生物医学信息研究中心，南京 210096)

为了快速计算整数型改进的离散余弦变换(IntMDCT)，构造了基于提升变换、模变换以及无穷范数旋转变换的3种计算12点IntMDCT的算法.首先将12点MDCT转化为6点Ⅳ型离散余弦变换(DCT－Ⅳ)，并将后者分解为7个Givens旋转变换的乘积;然后分别利用提升变换算法、模变换算法和无穷范数旋转变换算法实现Givens旋转变换的整数型近似计算;最后，对这3种算法在语音信号无损和有损压缩中的运行速度和计算精确度进行比较.实验结果表明，在这3种算法中，基于模变换的IntMDCT算法的运行速度最快;基于无穷范数旋转变换的IntMDCT算法的计算精度最高，并在有损音频压缩中获得的信噪比最高.

提升算法;模变换;无穷范数旋转变换;整数型MDCT;音频压缩

可逆的整数型变换可实现整数间的映射，因而被广泛应用于音频与图像的无损和有损压缩中.提升算法(lifting scheme)作为一种成熟的整数变换算法，普遍应用于整数型离散余弦变换(IntDCT)［1］以及整数型改进离散余弦变换(integer modified discrete cosine transform，IntMDCT)［2］中.

改进的离散余弦变换(MDCT)是基于第Ⅳ型离散余弦变换(DCT－Ⅳ)的重叠变换.MDCT的重叠性以及与DCT相似的能量压缩性使其能够有效地消除信号分块压缩时产生的边界伪影，因而被广泛应用于音频压缩标准中.例如，MPEG－1音频第3层编码(MP3)［3］采用 12点和 36点 MDCT;MPEG－4高级音频编码(AAC)［4］采用 256 点和2 048点MDCT.

近年来，MDCT的快速算法得到了迅速发展［5－9］.作为 MPEG 无损音频编码标准的关键部分，IntMDCT 受到高度重视［2，10－11］.现有的一维IntMDCT一般是先将MDCT矩阵或相应的DCT－Ⅳ矩阵分解为若干Givens旋转变换的乘积，再通过提升算法进行整数近似实现.然而，提升算法存在一定的缺陷，如由级联产生的延时和递增的取整误差等［12］.针对这些缺陷，Srinivasan［12］提出利用模变换(modulo transform)算法来取代提升算法.模变换算法利用勾股数三元组代替三角函数，对Givens旋转变换进行整数型近似，因而较提升算法具有更高的精度.Givens旋转变换在二维平面内的2范数不变性有利于扩展输出信号的动态范围.Yang等［13］提出了一种保持无穷范数不变性的无穷范数旋转变换(infinity norm rotation transform)，该变换可以有效控制输出信号的动态范围，且通过取整运算来得到整数至整数的映射，从而实现Givens旋转变换的整数型近似变换.

本文分别将提升算法、模变换和无穷范数旋转变换用于计算12点 IntMDCT，并对其在有损和无损音频压缩中的速度和精确度进行比较.

1 改进的离散余弦变换

对于长度为N的输入序列x(n)，其一维MDCT/IMDCT 定义如下［14］:

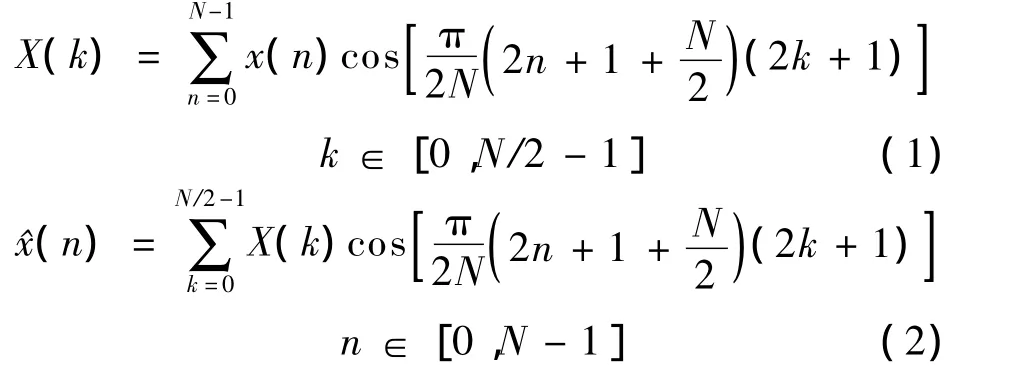
式中，N为4的倍数.

式(1)中MDCT的系数X(k)具有反对称性，即

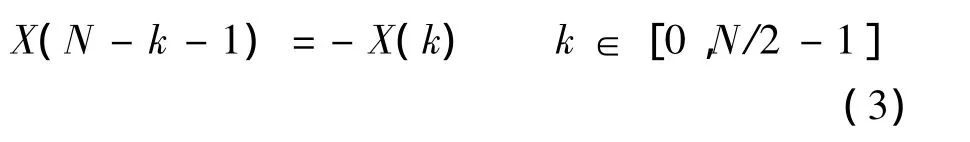
因此，只有N/2个线性独立的系数需要计算.式(2)中得到的(n)是时域混叠的，并非直接等于原始信号x(n)［14］.

利用文献［9－10］中的12点MDCT/IMDCT 将MDCT正交分解，信号流图见图1［10］.该算法先通过2级叠加将12点MDCT转化为6点DCT－Ⅳ，再利用3次Givens旋转变换将6点DCT－Ⅳ分解为一个3点第Ⅱ型离散余弦变换(DCT－Ⅱ)和一个3点第Ⅱ型离散正弦变换(DST－Ⅱ)，其中后者可分别由2次 Givens旋转变换实现.因此，12点MDCT可分解为7个 Givens旋转变换.逆变换IMDCT可通过信号流图转置得到.图1中的旋转系数(Ci，Si)均为无理数(见表1)，由计算机有限精度实现时必然产生截断误差，因此，由浮点型MDCT/IMDCT处理并重建的信号与原信号之间存在误差，无法做到完全重建.

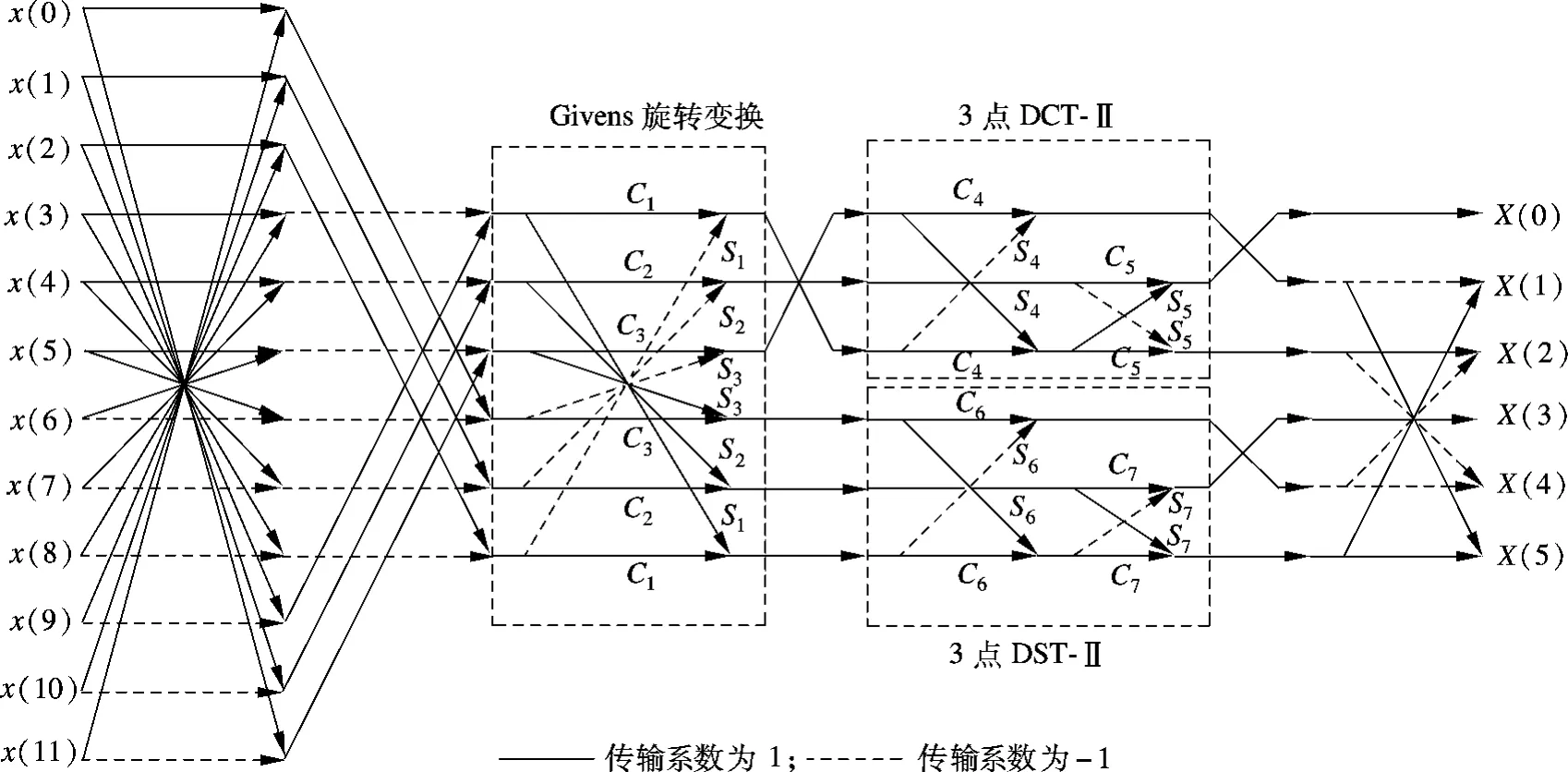
图112点MDCT/IMDCT的信号流图

文献［9－10］中的12点MDCT/IMDCT算法适用于计算MP3编码中的短窗MDCT.若直接将上述算法推广至长窗36点MDCT，会引入较多的旋转角度，使算法实现较为困难.为了解决这一问题，可以先采用文献［6－7］中的算法，将 36 点MDCT转化为3个长度为12点的MDCT，再对后者运用前面介绍的12点算法，便可得到36点MDCT.

表112点MDCT/IMDCT的旋转系数

2 12点MDCT的整数实现

2.1 提升算法

Givens旋转矩阵可以分解为3个三角矩阵的乘积.将三角矩阵与输入信号相乘称为提升运算，可用如下公式表示:

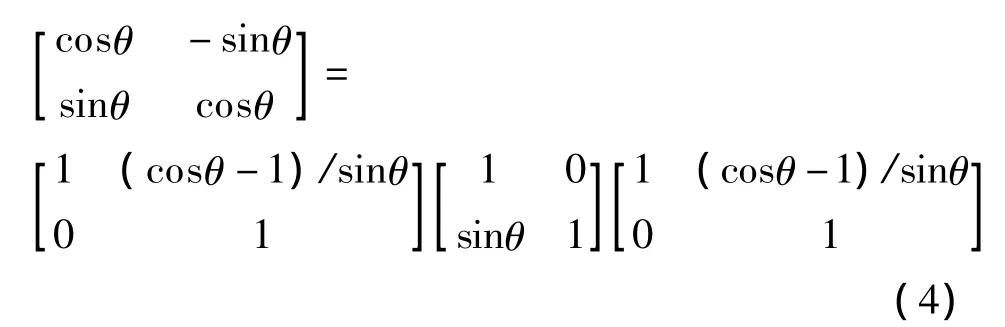
式(4)中，(cosθ－1)/sinθ和 sinθ即为提升系数(见图2).在每次提升过程中，通过取整可实现Givens旋转变换的整数型近似计算［15］.例如，第2次提升过程对输入(x1，x2)进行映射可表示为

图2 Givens旋转变换与提升结构实现

式(5)可近似为

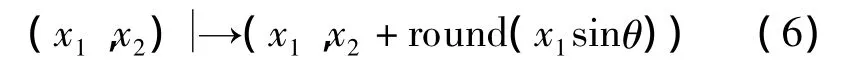
式中，round(·)表示取整.

更新后x1的值并未改变，因此仍能根据更新后的值计算出round(x1sinθ).式(6)的逆运算为

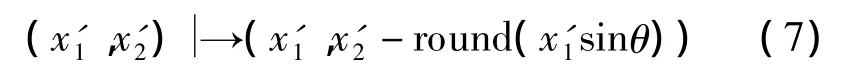
可见提升结构的整数近似是可逆的，且逆运算无误差.因此，通过三步提升方法实现的Givens旋转变换的整数近似是完全可逆的.

图1中的7个Givens旋转变换均可由提升算法实现［10］，总计算量为21次整数加法、21次实数乘法和21次取整运算.相应的提升系数可事先由有限精度求得，计算时查表使用.

2.2 模变换

模变换是通过整数矩阵]和整数尺度对Givens旋转矩阵]进行整数型近似的［12］，其中勾股数三元组满足.通过限定，可使模变换完全可逆，同时可减少计算量［12］.勾股数三元组(s，c，c+1)所对应的旋转角度θ=arctan(2s/(s2－1)).因此，旋转角度为θ的旋转矩阵可以进行如下整数型近似:

模变换的信号流图及相应的逆变换如图3所示.图中，运算符 sdiv 定义如下［12］:

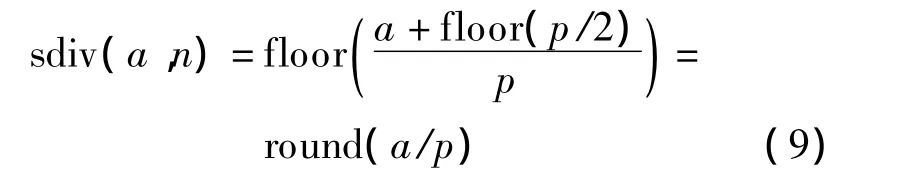
式中，floor(x)表示取不大于x的最大整数.

图3 基于勾股数三元组(s，c，c+1)的模变换及逆变换

根据式(9)，模变换可表示为［12］

计算式(10)时需要4次整数加法、2次整数乘法、2次整数除法和2次取整运算.

勾股数三元组能近似表示的角度见表2［12］.同一个旋转角度θ可利用不同的勾股数组进行不同精度的近似.此外，还可将θ分解为多个较小的角度之和，利用多个小角度模变换的级联近似表示角度为θ的模变换.因此，表1中的旋转系数可由表3中对应的勾股数三元组进行近似.图1中7个Givens旋转变换可用模变换进行整数型近似，从而代替传统的三步提升方法.用模变换计算7个Givens旋转变换的总运算量为44次整数加法、22次整数乘法、22次整数除法和22次取整运算.

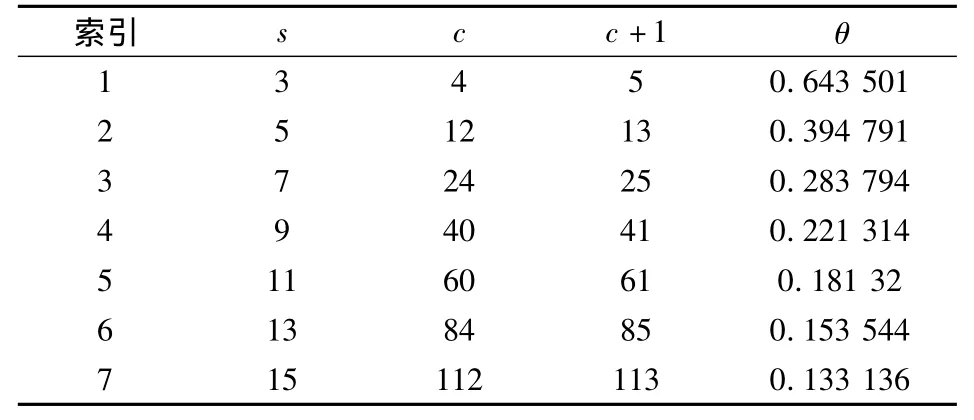
表2 勾股数组及其所能近似表示的角度

表312点MDCT/IMDCT的旋转系数对应的勾股数三元组

2.3 无穷范数旋转变换

提升算法和模变换都是对欧几里得空间内具有2范数不变性的Givens旋转变换的整数型近似计算.具有无穷范数不变性的旋转被称为无穷范数旋转变换［13］.在二维空间内，2范数和无穷范数旋转变换旋转一周的轨迹形状分别是一个圆形和一个正方形(见图4).二维空间内p范数旋转变换的旋转角θp可定义为游程与半径的比值［13］.当p=2时，θ2为Givens旋转角，游程为旋转划过的弧长，即图4中点A与点B'间的弧长，半径为圆半径;当p=∞时，θ∞为无穷范数旋转角，游程为旋转在正方形边上划过的距离，即图4中点A与点B间的线段长度，半径为正方形边长除以2.旋转一周后，θ2=2π，θ∞=8.因此，θ2和 θ∞之间存在如下的对应关系:

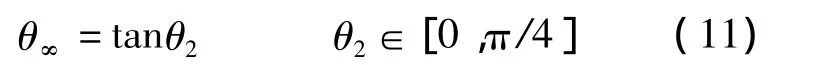
大于π/4的角度可以由多个小角度级联构成.

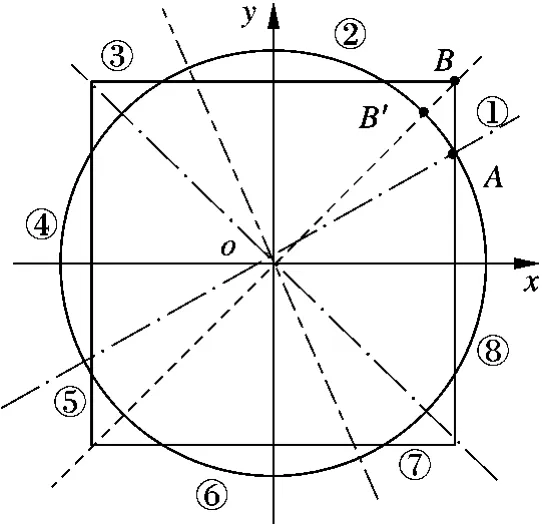
图4 无穷范数旋转变换的分段线性特性

为了计算无穷范数旋转变换，采用4条相交虚线将xoy平面划分为8个区域.每个区域内的无穷范数旋转变换均为基本线性变换，即错切变换、反射变换或错切变换(见图4).这种无穷范数旋转变换算法可表示为

式中，a为半径，即L为游程;∧为且运算.整数输入x，y与实数θ∞相乘可得到实数输出.为了实现整数到整数的映射，需要引入一次取整运算.整数型无穷范数旋转变换的单次计算量为1次整数加法、1次实数乘法和1次取整运算，或2次整数加法、1次实数乘法、1次整数移位和1次取整运算.与提升算法和模变换算法不同的是，这里的取整运算会使该旋转的逆运算产生误差.

由此可见，图1中的7个Givens旋转变换可以转化为无穷范数旋转变换进行整数型近似.

3 算法效果比较

分别对基于提升算法、模变换和无穷范数旋转变换的12点IntMDCT/IntIMDCT在语音信号无损和有损压缩中的效果进行比较.测试信号为一段时长为2.9 s、采样频率为8 kHz、8 bit整数编码的真实语音序列，其波形图如图5(a)所示.效果评价指标为均方误差(mean square error，MSE)和信噪比(signal to noise ratio，SNR).测试环境为AMD 3.0 GHz CPU，Windows Server 2008系统和Matlab 7.9.基于提升变换［10］、模变换［12］、无穷范数旋转变换［13］的IntMDCT分别简记为算法1、算法2和算法3.

图5 3种算法在有损语音压缩中的效果比较

一维信号的均方误差定义为

式中，em表示第m时刻时理想信号Ym与重建信号m之差，即em=Ym－m;M表示信号的长度.

一维信号的信噪比定义为

3.1 无损压缩

分别对测试音频信号运行这3种算法，得到的变换系数不经量化，直接进行12点 IntIMDCT并重建原始信号.对3种算法的运行时间和所得重建信号的均方误差进行比较，结果见表4.由于模变换只涉及整数计算，因此算法2的速度最快:其正变换时间较算法1快92.9%，较算法3快66.0%;其反变换时间较算法1快87.3%，较算法3快56.6%.算法1和算法2在无损压缩中不产生任何误差，但算法3会产生少量误差.

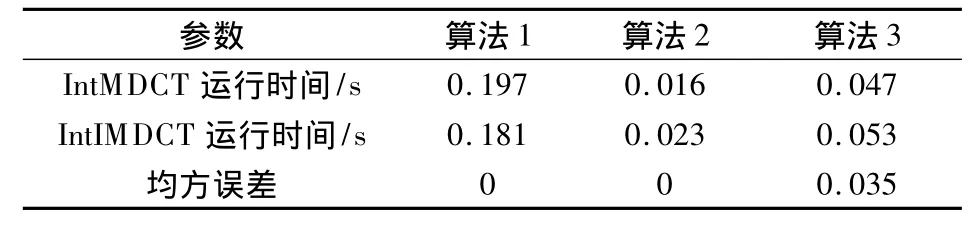
表4 3种算法在无损音频压缩中的运行时间和均方误差

3.2 有损压缩

分别对测试信号运行这3种算法，得到的变换系数进行3～8 bit均匀量化.量化公式为

式中，q为量化比特数.对量化后的系数进行逆量化和12点IntIMDCT，并重建信号.

对这3种算法的运行时间和所得重建信号的信噪比进行比较，结果见表5.由于有损压缩的运行时间与表4相同，此处不再一一列出.由表5可知，由于算法3能有效控制输出的动态范围，因此在有损压缩中得到了最高的信噪比.例如，在低比特(5 bit以下)均匀压缩时，算法3实现的信噪比较算法1和算法2提高了1.5～2.2 dB.此外，算法2的取整运算次数少于算法1，导致其取整误差略小于算法1.因此，在大部分情况下，算法2在有损压缩中的信噪比较算法1略高.图5(b)～(d)给出了5 bit均匀量化时利用这3种算法得到的重建信号及误差.图中黑色部分为信号，灰色部分为误差.由图可知，算法3的误差小于其他2种算法.

表5 3种算法在有损音频压缩中的信噪比 dB

4 结语

本文将提升算法、模变换和无穷范数旋转应用于12点整数型MDCT，并对基于这3种算法的IntMDCT在语音信号无损和有损压缩中的速度和精确度进行了比较.实验结果表明，基于模变换的IntMDCT运算速度最快，基于无穷范数旋转变换的IntMDCT的运算速度次之，基于提升算法的IntMDCT算法的运算速度最慢.在无损压缩中，提升算法和模变换均不产生误差，而无穷范数旋转变换产生少量误差.在有损压缩中，无穷范数旋转变换由于能够有效控制输出的动态范围，因而能实现最高的信噪比.

［1］ Zeng Y，Cheng L，Bi G.Integer DCTs and fast algorithms［J］.IEEE Transactions on Signal Processing，2001，49(19):2774－2782.

［2］ Huang H，Rahardja S，Yu R.Integer MDCT with enhanced approximation of the DCT－Ⅳ［J］.IEEE Transactions on Signal Processing，2006，54(11):1156－1159.

［3］林福宗.多媒体技术基础［M］.北京:清华大学出版社，2000.

［4］ Pereira F，Ebrahimi T.The MPEG-4book［M］.Upper Saddle River，USA:Prentice Hall，2002.

［5］Britanak V.New universal rotation — based fast computational structures for an efficient implementation of the DCT－Ⅳ/DST－Ⅳ and analysis/synthesis MDCT/MDST filter banks［J］.Signal Processing，2009，89(11):2213－2232.

［6］ Shu H，Bao X，Toumoulin C.Radix－3 algorithm for the fast computation of forward and inverse MDCT［J］.IEEE Signal Processing Letters，2007，14(10):93－96.

［7］ Wu J，Shu H.Mixed－radix algorithm for the computation of forward and inverse MDCTs［J］.IEEE Transactions on Circuits and SystemsⅠ:Regular Papers，2009，56(4):784－794.

［8］ Britanak V.New fast computational structures for an efficient implementation of the forward/backward MDCT in MP3 audio coding standard ［J］.Signal Processing，2010，90(2):536－547.

［9］ Britanak V.A survey of efficient MDCT implementations in MP3 audio coding standard:retrospective and state－of－the－art［J］.Signal Processing，2011，91(4):624－672.

［10］ Krishnan T，Oraintara S.Fast and lossless implementation of the forward and inverse MDCT computation in MPEG audio coding［C］//IEEE International Symposium on Circuits and Systems.Phoenix，AZ，USA，2002:181－184.

［11］ Li J.Low noise reversible MDCT(RMDCT)and its application in progressive－to－lossless embedded audio coding ［J］.IEEE Transactions on Signal Processing，2005，53(5):1870－1880.

［12］ Srinivasan S.Modulo transforms— an alternative to lifting ［J］.IEEE Transactions on Signal Processing，2006，54(13):1864－1874.

［13］ Yang L，Hao P.Infinity－norm rotation transforms［J］.IEEE Transactions on Signal Processing，2009，57(7):2594－2603.

［14］ Princen J P，Johnson A W，Bradley A B.Subband/transform coding using filter bank designs based on time domain aliasing cancellation［C］//IEEE International Conference on Acoustics，Speech，and Signal Processing.Dallas，Texas，USA，1987:2161－2164.

［15］ Geiger R，Sporer T，Koller J.Audio coding based on integer transforms［C］//The111th Audio Engineering Society Convention.New York，USA，2001:5471－5479.

Comparison of three IntMDCT algorithms in audio compression

Wang Lü1，3Wu Jiasong1，2，3Senhadji Lotfi2，3Shu Huazhong1，3

(1Laboratory of Image Science and Technology，Southeast University，Nanjing 210096，China)
(2Laboratoire Traitement du Signal et de I'Image，Université de Rennes 1，Rennes 35042，France)
(3Centre de Recherche en Information Biomédicale Sino－Français，Nanjing 210096，China)

In order to improve the computation efficiency of the integer modified discrete cosine transform(IntMDCT)，three algorithms based on the lifting scheme，modulo transform and infinity norm rotation transform are formulated respectively for computing the 12－point IntMDCT.First，the 12－point IntMDCT is converted into the 6－point type－Ⅳ discrete cosine transform(DCT－Ⅳ)，which is then factorized into a product of 7 Givens rotation matrices.The integer type Givens rotation matrices are approximated by lifting scheme，modulo transform and infinity norm rotation transform，respectively.Finally，the speed and accuracy of these three IntMDCT algorithms are compared in both lossless and lossy audio compression.The experimental results show that in the three algorithms，the IntMDCT algorithm based on the modulo transform has the highest computation speed.The IntMDCT algorithm based on the infinity norm rotation transform has the highest accuracy，and can achieve the highest signal to noise ratio(SNR)in lossy audio compression.

lifting scheme;modulo transform;infinity norm rotation;integer modified discrete cosine transform;audio compression

TP391

A

1001－0505(2012)02－0259－06

10.3969/j.issn.1001－0505.2012.02.013

2011－09－08.

王膂(1986—)，男，硕士生;舒华忠(联系人)，男，博士，教授，博士生导师，shu.list@seu.edu.cn.

国家自然科学基金资助项目(61073138，60873048)、国家自然科学基金国际合作与交流资助项目(60911130370).

王膂，伍家松，Senhadji Lotfi，等.音频压缩中3种整数型MDCT变换的比较［J］.东南大学学报:自然科学版，2012，42(2):259－264.［doi:10.3969/j.issn.1001－0505.2012.02.013］